Filtri analogici
1) Caratteristiche della risposta in ampiezza di un filtro passa basso :
- Banda passante
- Ripple in banda passante
- Banda oscura
- Ripple in banda oscura
- Regione di transizione
2) Filtri a fase lineare :
Sono filtri per i quali la risposta in fase ![]() cresce linearmente con la frequenza, in tal modo si ha che tutte le frequenze in ingresso sono ritardate della stessa entità.
cresce linearmente con la frequenza, in tal modo si ha che tutte le frequenze in ingresso sono ritardate della stessa entità.
3) Caratteristiche della risposta al gradino :
- Tempo di salita
- Tempo di settling
- Sovraelongazione
- Oscillazioni
4) Trasformazioni che danno luogo ad un segnale fedele :
Le uniche trasformazioni ammesse sono un guadagno k ed un ritardo δ ossia ![]() .
.
5) Filtri analogici e sistemi LTI :
Un filtro analogico è un sistema LTI pertanto vale la relazione ![]() .
.
6) Filtro di Butterworth :
Si tratta di filtri massimamente piatti nella banda passante con risposta in frequenza 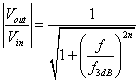 essendo n l'ordine del filtro. Si può anche utilizzare l'espressione normalizzata
essendo n l'ordine del filtro. Si può anche utilizzare l'espressione normalizzata 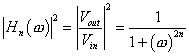 essendo
essendo ![]() la frequenza normalizzata. I filtri di Butterworth hanno la caratteristica di non essere a fase lineare e di richiedere un ordine elevato per avere una regione di transizione sufficientemente ripida.
la frequenza normalizzata. I filtri di Butterworth hanno la caratteristica di non essere a fase lineare e di richiedere un ordine elevato per avere una regione di transizione sufficientemente ripida.
7) Polinomio di Chebyschev :
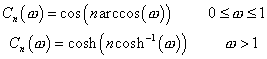
Alternativamente possono essere definiti in forma ricorsiva essendo ![]() ,
, ![]() ed in generale
ed in generale ![]() .
.
8) Filtro di Chebyshev :
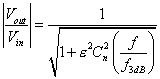 dove l'ampiezza del ripple in banda utile è
dove l'ampiezza del ripple in banda utile è ![]() , ha la caratteristica di non aver fase lineare e di consentire una maggiore piattezza in banda utile rispetto ai filtri Butterworth, a parità di ordine.
, ha la caratteristica di non aver fase lineare e di consentire una maggiore piattezza in banda utile rispetto ai filtri Butterworth, a parità di ordine.
9) Filtro di Chebyshev inverso :
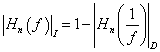
ne deriva che il ripple non è più in banda utile ma in banda oscura e vale ![]() .
.
10) Filtri ellittici :
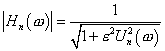
dove ![]() è una funzione ellittica Jacobiana, sono filtri caratterizzati da una risposta in banda massimamente piatta per un dato ordine ma risposta in fase estremamente non lineare.
è una funzione ellittica Jacobiana, sono filtri caratterizzati da una risposta in banda massimamente piatta per un dato ordine ma risposta in fase estremamente non lineare.
11) Filtri di Bessel :
Sono caratterizzati dall'aver massima linearità della risposta in fase in banda passante.
12) Trasformazione da passa basso a passa alto :
Se per il passa basso la variabile complessa è ![]() e per il passa alto la variabile complessa è
e per il passa alto la variabile complessa è ![]() la trasformazione è
la trasformazione è ![]() che considerando il comportamento a regime cioè
che considerando il comportamento a regime cioè ![]() comporta
comporta ![]() e
e ![]() .
.
13) Trasformazione da passa basso a passa banda :
Se per il passa basso la variabile complessa è ![]() e per il passa banda la variabile complessa è
e per il passa banda la variabile complessa è ![]() la trasformazione è
la trasformazione è ![]() , anche in questo caso a regime si ha
, anche in questo caso a regime si ha ![]() ed
ed ![]() e si ottiene una equazione di secondo grado
e si ottiene una equazione di secondo grado 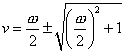 la quale ha due soluzioni per v.
la quale ha due soluzioni per v.
