Analisi di circuiti non lineari a microonde
1) Tensione v(t) di un circuito RC parallelo alimentato da un generatore di corrente :
L´espressione nel dominio del tempo si ottiene risolvendo la equazione differenziale ![]() che fornisce
che fornisce 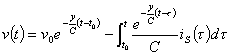 . Si può avere anche una espressione in termini di fasori
. Si può avere anche una espressione in termini di fasori ![]() da cui
da cui ![]() .
.
2) Soluzione numerica diretta della 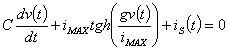 :
:
L´equazione differenziale non lineare viene discretizzata nel dominio del tempo, l´equazione che ne risulta può assumere le due seguenti forme :
a) 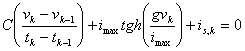 in questo caso occorre un valore iniziale per poter calcolare poi iterativamente gli altri valori, tuttavia è insita una imprecisione in quanto la non linearità prevede la conoscenza di vk e quindi si dovrà risolvere una equazione non lineare nella quale la soluzione è in forma implicita, essa viene trovata con metodi iterativi come quello di Newton. L´errore può essere reso piccolo a piacere riducendo l´intervallo di discretizzazione.
in questo caso occorre un valore iniziale per poter calcolare poi iterativamente gli altri valori, tuttavia è insita una imprecisione in quanto la non linearità prevede la conoscenza di vk e quindi si dovrà risolvere una equazione non lineare nella quale la soluzione è in forma implicita, essa viene trovata con metodi iterativi come quello di Newton. L´errore può essere reso piccolo a piacere riducendo l´intervallo di discretizzazione.
b) 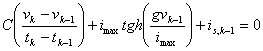 in questo caso se vk-1 è noto si può risolvere per vk in quanto l´equazione diviene lineare nell´incognita. La stabilità della soluzione non può essere garantita anche se rendiamo molto piccolo l´intervallo di discretizzazione.
in questo caso se vk-1 è noto si può risolvere per vk in quanto l´equazione diviene lineare nell´incognita. La stabilità della soluzione non può essere garantita anche se rendiamo molto piccolo l´intervallo di discretizzazione.
Il passo di discretizzazione può essere reso uniforme o meno, in genere conviene un passo uniforme per il regime permanente mentre per il transitorio dove ci sono variazioni più brusche conviene un passo più stretto.
3) Soluzione mediante espansione in serie della 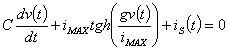 :
:
In alternativa alla discretizzazione temporale si possono fare delle ipotesi sulla soluzione come il richiedere che sia esprimibile in serie di potenze e che questa serie sia troncabile in modo da mantenere la maggior parte della informazione, alla fine si dovrà risolvere l´equazione per ogni termine della serie.
4) Serie di Volterra :
È una estensione della integrale di convoluzione ![]() ai circuiti non lineari , si ha
ai circuiti non lineari , si ha ![]() dove hn è il nucleo di ordine n avente trasformata di Fourier generalizzata
dove hn è il nucleo di ordine n avente trasformata di Fourier generalizzata ![]() . Nel domino di Fourier la serie di Volterra assume la forma
. Nel domino di Fourier la serie di Volterra assume la forma ![]() , ne consegue che lo spettro del segnale d´uscita è diverso dallo spettro del segnale d´ingresso.
, ne consegue che lo spettro del segnale d´uscita è diverso dallo spettro del segnale d´ingresso.
Nel caso di un segnale d´ingresso reale il nucleo di secondo ordine da luogo ad un termine rettificato oltre che alla armonica di secondo ordine.
5) Probing Method :
Si tratta di un metodo che consente di determinare i nuclei del sistema, i passi di applicazione sono i seguenti :
a) si applica un tono ideale ![]() la risposta è
la risposta è ![]() arrestandosi per semplicità al secondo ordine e sostituendola nell´equazione differenziale che descrive il circuito contenente la non-linearità espressa in serie di potenze, si ottiene un´equazione contenente termini a diverse frequenze, essa deve essere verificata per ogni frequenza, dall´uguaglianza alla frequenza fondamentale si ottiene il nucleo di ordine 1.
arrestandosi per semplicità al secondo ordine e sostituendola nell´equazione differenziale che descrive il circuito contenente la non-linearità espressa in serie di potenze, si ottiene un´equazione contenente termini a diverse frequenze, essa deve essere verificata per ogni frequenza, dall´uguaglianza alla frequenza fondamentale si ottiene il nucleo di ordine 1.
b) Per ricavare il termine generale di ordine 2 applichiamo due toni ideali ![]() , stavolta si ha :
, stavolta si ha : ![]() consideriamo i soli termini che contengono il nucleo di ordine 2 nella forma più generale contenete cioè sia f1 che f2
consideriamo i soli termini che contengono il nucleo di ordine 2 nella forma più generale contenete cioè sia f1 che f2
c) Si ricavano gli altri termini in maniera iterativa
Naturalmente il metodo richiede che la non linearità sia espressa in termini di serie di potenze e che la non linearità sia lieve altrimenti il calcolo dei nuclei risulta impraticabile.
6) 1dB Compression Point :
È il valore della potenza in ingresso per il quale la potenza in uscita vale 1dB in meno rispetto al valore della potenza di uscita in saturazione.
7) Intercept Point :
Nel piano in dB che lega la potenza in uscita alla potenza in ingresso, abbiamo una retta a pendenza unitaria per il termine di primo grado e delle rette con pendenze diverse per i termini degli altri gradi , gli intercept point che si utilizzano in genere sono quelli tra la retta relativa al primo grado e quelle relative al 2° grado ed al 3° grado.
8) Problemi legati alla intermodulazione :
I contributi della intermodulazione cadono nella banda del segnale d´ingresso e quindi non è possibile filtrarli.
9) Problemi legati alla desensitivizzazione :
Viene sottratta potenza alla fondamentale e ridistribuita sullo spettro, ciò fa si che nel caso di più toni la compressione arriva prima.
10) Serie di Fourier :
In questo caso l´incognita viene espressa in serie di Fourier ![]() e sostituita nell´equazione differenziale che descrive il circuito, per ogni termine della serie si ottiene una equazione algebrica, ci si può limitare ad un numero finito a patto che i primi termini della serie siano in grado di descrivere adeguatamente la funzione.
e sostituita nell´equazione differenziale che descrive il circuito, per ogni termine della serie si ottiene una equazione algebrica, ci si può limitare ad un numero finito a patto che i primi termini della serie siano in grado di descrivere adeguatamente la funzione.
La parte reale delle equazioni si può calcolare in maniera immediata moltiplicando per una opportuna matrice mentre la parte non lineare deve essere calcolata nel dominio del tempo e poi trasformata.
È come suddividere il circuito in parte lineare e parte non lineare dopodiché si eguagliano le correnti per ogni armonica , dalle equazioni che si ottengono si può ricavare l´incognita mediante il metodo di Newton.
Il metodo consente di trattare anche circuiti con forti non linearità tuttavia non è possibile la analisi del transitorio e con segnali d´ingresso complessi.
