Calcolo della trasformata di Fourier discreta

1) Formule della DFT :

                    per k = 0, 1,  … , N-1

            per n = 0, 1,  … , N-1

 

2) Proprietà di  utilizzate per migliorare l´efficienza del calcolo della DFT :

                                                        

 

3) Algoritmo di Goertzel  :

                        dove      

è un algoritmo che richiede 4N moltiplicazioni reali e 4N addizioni reali per ricavare X(k) per ogni k.

Un miglioramento della complessità si ottiene mediante la algoritmo di Goertzel modificato basato sulla funzione di trasferimento  .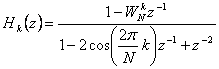

 

4) Algoritmo di FFT basato sulla decimazione nel tempo :

In sostanza la sequenza x(n) viene scomposta in sottosequenze via via più piccole in particolare al primo passo si costituiscono due sequenze ciascuna da N/2 punti , una relativa ai pari e la altra relativa ai dispari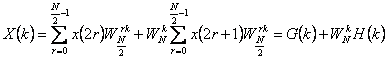

 

5) Equazioni di una farfalla nel tempo :

 

6) Algoritmo di FFT basato sulla decimazione in frequenza :

In sostanza la sequenza X(k) viene scomposta in sottosequenze via via più piccole in particolare al primo passo si costituiscono due sequenze ciascuna da N/2 punti , una relativa ai pari e la altra relativa ai dispari

 

7) Equazioni di una farfalla in frequenza :

 

8) Algoritmo della Trasformata Z Chirp :

Consente di calcolare la trasformata Z di una generica sequenza non unicamente sul cerchio unitario ma nei punti  (… con    e    )   i quali al variare di k da 0 ad M-1 descrivono una spirale , la trasformata in questi punti vale 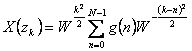  si presenta cioè come una convoluzione della sequenza  si può quindi pensare ad un filtro Chirp con risposta al campione unitario  , si tratta di una sequenza a durata infinita pertanto per calcolare la FFT è necessaria una sua segmentazione.