Giunzione PN
1) Analisi di un semiconduttore drogato in maniera arbitraria :
La presenza di un gradiente di concentrazione di portatori dà luogo ad una corrente di diffusione dalla regione a maggiore concentrazione verso la regione a minore concentrazione, i portatori che si spostano però lasciano degli ioni di segno opposto, la distribuzione di carica che si ottiene dà luogo ad un campo elettrico che si oppone all´ulteriore flusso di elettroni pertanto all´equilibrio il semiconduttore è caratterizzato da una concentrazione di portatori ancora variabile con la posizione e da un potenziale di Built-In. La presenza di un campo elettrico si deduce facilmente osservando che sui diagrammi a bande l´energia che separa il livello di Fermi dalla banda di conduzione è energia potenziale mentre la differenza di energia tra la banda di conduzione e l´energia della elettrone è energia cinetica di quest´ultimo, pertanto definendo come potenziale ![]() e ricordando la relazione tra potenziale e campo si ha
e ricordando la relazione tra potenziale e campo si ha ![]() in quanto Ef è costante in un semiconduttore all´equilibrio termico e quindi la sua derivata è nulla mentre Ei si trova al centro tra banda di valenza e banda di conduzione e pertanto varia se il semiconduttore ha drogaggio variabile.
in quanto Ef è costante in un semiconduttore all´equilibrio termico e quindi la sua derivata è nulla mentre Ei si trova al centro tra banda di valenza e banda di conduzione e pertanto varia se il semiconduttore ha drogaggio variabile.
All´equilibrio termico la corrente che scorre nel semiconduttore deve essere in media nulla quindi dall´equazione di Drift & Diffusion ![]() si ottiene
si ottiene ![]() del resto essendo
del resto essendo ![]() uguagliando le due espressioni trovate si ottiene
uguagliando le due espressioni trovate si ottiene ![]() che integrata tra due punti a diversa concentrazione fornisce
che integrata tra due punti a diversa concentrazione fornisce ![]() oppure in forma esponenziale
oppure in forma esponenziale ![]() .
.
2) Equazione di Poisson per un semiconduttore con un generico drogaggio e sua semplificazione :
![]()
dove si è sostituito ![]() e
e ![]() . L´equazione non è risolvibile nel caso generale pertanto spesso vengono adottate due semplificazioni :
. L´equazione non è risolvibile nel caso generale pertanto spesso vengono adottate due semplificazioni :
a) Approssimazione di quasi-neutralità , in sostanza si assume che la concentrazione di portatori sia pressoche uguale alla concentrazione delle impurezze, essa è quanto mai valida nel bulk dove quindi a seconda del drogaggio del semiconduttore si ha n = Nd oppure p = Na .
b) Approssimazione di Depletion, prevede che la concentrazione di portatori liberi sia molto inferiore alla concentrazione delle impurezze ionizzate, in sostanza n << Nd oppure p << Na .
3) Giunzione PN all´equilibrio termico :
Quando si mette a contatto un p_doped con un n_doped si ha una brusca variazione del drogaggio in corrispondenza della giunzione pertanto si ha un flusso di elettroni dalla regione n alla regione p ed un flusso di lacune in verso opposto, pertanto nelle regioni di provenienza rimangono degli ioni i quali generano un campo elettrico che si oppone all´ulteriore diffusione di carica. Per analizzare questa situazione si utilizza la approssimazione di quasi neutralità nel bulk e la approssimazione di Depletion nella regione di carica spaziale posta a ridosso della giunzione, in essa quindi l´equazione di Poisson si riduce a ![]() , la utilizziamo per trovare il campo elettrico. Nell´n_doped Na=0 pertanto
, la utilizziamo per trovare il campo elettrico. Nell´n_doped Na=0 pertanto ![]() integrandola per 0 < x < xn ossia nella regione di carica spaziale della n_doped si ha
integrandola per 0 < x < xn ossia nella regione di carica spaziale della n_doped si ha ![]() , analogamente per il p_doped si trova
, analogamente per il p_doped si trova ![]() quindi dovendo essere il campo continuo nell´origine altrimenti non potrebbe ammettere un potenziale, si trova la relazione
quindi dovendo essere il campo continuo nell´origine altrimenti non potrebbe ammettere un potenziale, si trova la relazione ![]() che in sostanza mostra come il semiconduttore maggiormente drogato abbia una minore estensione della regione di depletion.
che in sostanza mostra come il semiconduttore maggiormente drogato abbia una minore estensione della regione di depletion.
Integrando ulteriormente il campo si ottiene nell´n_doped il potenziale ![]() mentre nel p_doped
mentre nel p_doped ![]() dove xn ed xp sono i potenziali agli estremi della regione di Depletion e la loro differenza corrisponde al potenziale di Built_In
dove xn ed xp sono i potenziali agli estremi della regione di Depletion e la loro differenza corrisponde al potenziale di Built_In ![]() .
.
4) Potenziale di Built-In per una giunzione p+n :
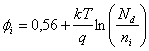
questo perché nel caso di un semiconduttore molto drogato il livello di Fermi è molto vicino ad una delle due bande.
5) Giunzioni PN polarizzata inversamente :
Applicando una polarizzazione inversa ossia il + del generatore sulla regione n si aumentano le dimensioni della regione di Depletion, per essa infatti si ha 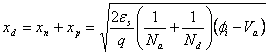 come pure il campo elettrico per il quale si ha
come pure il campo elettrico per il quale si ha ![]() mentre la capacità diminuisce in quanto si allontanano le armature, si ha
mentre la capacità diminuisce in quanto si allontanano le armature, si ha 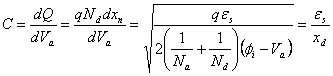 che è la classica capacità per piccoli segnali.
che è la classica capacità per piccoli segnali.
Naturalmente dato che aumentando la polarizzazione inversa aumenta il campo elettrico, deve avvenire qualche fenomeno o rottura che limiti il funzionamento, in particolare prima della rottura del dispositivo si possono presentare i seguenti effetti :
Effetto Valanga Il campo elettrico applicato accelera un portatore libero il quale si scontra con un atomo e ne libera un elettrone di valenza. A seguito della urto si hanno 3 portatori, due elettroni ed una lacuna i quali vengono accelerati dal campo nuovamente dando luogo ad altri urti.
Effetto Zener Se il semiconduttore è molto drogato si verifica l´effetto Zener prima della effetto Valanga, in particolare si ha che essendo la regione di carica spaziale molto piccola, il campo elettrico è talmente elevato da rompere dei legami covalenti e creare delle coppie elettrone-lacuna.
