Elementi di elaborazione dei segnali
Trasformazioni lineari tempo invarianti
1) Funzione di trasferimento del quadripolo complementare al quadripolo avente funzione di trasferimento H(f) :
![]()
infatti il quadripolo possiede sicuramente un ritardo che posto al denominatore diviene un anticipo e va quindi neutralizzato tramite l´esponenziale complesso negativo. Un segnale che attraversi un quadripolo ed il suo complementare giunge pertanto in uscita soltanto attenuato.
2) Elaborazione lineare di campioni :
Un segnale s(t) può essere rappresentato nella forma campionata 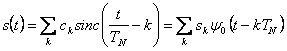 , dove
, dove ![]() è una funzione di base ad energia unitaria. Applicando in ingresso ad un quadripolo LTI la sequenza campionata x(n) si ottiene la risposta ancora in termini di campioni
è una funzione di base ad energia unitaria. Applicando in ingresso ad un quadripolo LTI la sequenza campionata x(n) si ottiene la risposta ancora in termini di campioni ![]() dove h(n) è la risposta impulsiva discreta equivalente. Affinché vi sia reversibilità è necessario che i due quadripoli abbiano la stessa banda ma lo spettro può avere andamento diverso, ricordando infatti che lo spettro di un processo campionato in banda base è
dove h(n) è la risposta impulsiva discreta equivalente. Affinché vi sia reversibilità è necessario che i due quadripoli abbiano la stessa banda ma lo spettro può avere andamento diverso, ricordando infatti che lo spettro di un processo campionato in banda base è ![]() lo spettro di uscita PY(f) ha la stessa espressione ma la covarianza cxx è in genere diversa.
lo spettro di uscita PY(f) ha la stessa espressione ma la covarianza cxx è in genere diversa.
Trasformazioni in segnale squadrato
3) Segnale squadrato :
I flussi numerici sono in genere veicolati dal segnale reale in forma squadrata ![]() dove xqk può assumere soltanto valori appartenenti ad un insieme discreto, riuscendo a portare in questa forma anche i segnali analogici si è in grado di effettuare un´unica trattazione delle possibili elaborazioni. Il teorema di Nyquist ci garantisce la possibilità di sostituire il segnale con dei suoi campioni prelevati con una frequenza doppia rispetto alla massima frequenza presente nel segnale quindi è ammissibile in via teorica la formazione di un segnale in forma squadrata
dove xqk può assumere soltanto valori appartenenti ad un insieme discreto, riuscendo a portare in questa forma anche i segnali analogici si è in grado di effettuare un´unica trattazione delle possibili elaborazioni. Il teorema di Nyquist ci garantisce la possibilità di sostituire il segnale con dei suoi campioni prelevati con una frequenza doppia rispetto alla massima frequenza presente nel segnale quindi è ammissibile in via teorica la formazione di un segnale in forma squadrata ![]() ottenuto da x(t) mediante un formatore di segnale squadrato
ottenuto da x(t) mediante un formatore di segnale squadrato ![]() sostanzialmente costituito da un interruttore che campiona all´istante t0 , un integratore che mantiene ed in uscita da esso un interruttore verso massa che chiude a t+T0 . Purtroppo il quadripolo complementare che dovrebbe garantire la reversibilità ha funzione di trasferimento
sostanzialmente costituito da un interruttore che campiona all´istante t0 , un integratore che mantiene ed in uscita da esso un interruttore verso massa che chiude a t+T0 . Purtroppo il quadripolo complementare che dovrebbe garantire la reversibilità ha funzione di trasferimento ![]() che presenta una discontinuità nel guadagno che richiede una selettività infinita e quindi è estremamente difficile da realizzare. Soltanto nel caso di un flusso numerico il quadripolo complementare è estremamente semplice e consiste in un ulteriore formatore di segnale squadrato avente la stessa temporizzazione , tuttavia in presenza di disturbi si ha una rigenerazione solo formale che deve essere seguita da una procedura di decisione.
che presenta una discontinuità nel guadagno che richiede una selettività infinita e quindi è estremamente difficile da realizzare. Soltanto nel caso di un flusso numerico il quadripolo complementare è estremamente semplice e consiste in un ulteriore formatore di segnale squadrato avente la stessa temporizzazione , tuttavia in presenza di disturbi si ha una rigenerazione solo formale che deve essere seguita da una procedura di decisione.
4) Caratteristiche spettrali del processo con realizzazione in forma squadrata :
A partire da un processo X(t) limitato in banda si ottiene un segnale in forma squadrata avente densità spettrale ![]() che è in relazione con la densità spettrale del processo entrante mediante la
che è in relazione con la densità spettrale del processo entrante mediante la ![]() .
.
Principi di codifica
5) Codifica con ridondanza :
È una codifica che si applica col fine di migliorare le prestazioni di un sistema di trasmissione imperfetto, in particolare viene indipendentemente dalle caratteristiche della modulazione impiegata nel sistema di trasmissione, vengono inseriti dei bit in eccesso al fine di consentire la rivelazione della errore che può portare alla correzione dello stesso (FEC) oppure alla richiesta di ritrasmissione, in ogni caso si ha un miglioramento del BER ossia il valore atteso del rapporto tra il numero dei bit errati appartenenti ad una sequenza molto lunga e il n° dei bit che compongono la sequenza stessa.
L´aggiunta di bit in eccesso provoca un aumento del ritmo binario in uscita Rx rispetto a quello in ingresso Ru e viene espresso mediante la frequenza di codifica ![]() dove n è il numero di cifre che compongono la parola in ingresso al codificatore mentre k è il numero di cifre della parola corrispondentemente emessa dal codificatore.
dove n è il numero di cifre che compongono la parola in ingresso al codificatore mentre k è il numero di cifre della parola corrispondentemente emessa dal codificatore.
Le tecniche di codifica con ridondanza principali sono la codifica lineare a blocchi e la codifica convoluzionale.
6) Codifica lineare a blocchi :
A partire da una sequenza binaria u(n) il codificatore forma un blocco costituito da k bit in un registro di ugual grandezza, mediante combinazioni lineari di questi bit viene formata una parola di codice x in un registro con n > k bit .
Si ha così che 2n-2k configurazioni che non appartengono al codice vengono prodotte soltanto da un errore e pertanto vengono rilevate e possibilmente corrette dal decodificatore.
7) Codifica sistematica :
È una delle possibili codifiche lineari a blocchi, in sostanza i primi k bit della parola formata dal codificatore sono uguali ai k bit della parola u d´ingresso mentre i restanti n-k bit vengono ottenuti dai precedenti mediante combinazioni lineari in aritmetica modulo 2.
Un esempio di codifica sistematica è la codifica (2,1) di Manche ster essa associa alla parola u = 0 in ingresso la parola
y = 01 in uscita ed alla parola u = 1 la parola y =10 mentre le parole y = 11 ed y = 00 si presentano al decodificatore soltanto in caso di errore che tuttavia non può essere corretto in quanto non si può capire quale dei due bit della coppia sia quello errato. Un altro esempio di codifica sistematica è la codifica (7,4) di Hamming nella quale i restanti 3 bit della parola prodotta dal codificatore sono il bit 5 u1Å u2 Å u3 , il bit 6 u2Åu3Åu4 ed il bit 7 u1Åu2Åu4 in tal modo grazie alla notevole ridondanza si ha che le parole di codice differiscono tra di loro almeno in 3 posizioni quindi è possibile rivelare la presenza di uno o due errori e correggerne uno.
8) Codifica convoluzionale :
Si tratta di una codifica con memoria si ha infatti che la sequenza d´ingresso u(n) va a riempire un registro ad L bit , da questo mediante combinazioni lineari in aritmetica modulo 2 si formano n bit che poi vengono serializzati andando a formare la sequenza codificata x(n) in sostanza per ogni cifra binaria d´ingresso se ne producono n-1 ridondanti il che determina che il ritmo binario in uscita è n volte maggiore del ritmo binario in ingresso, tale fattore può essere ridotto parallelizzando la parola u(n) ed andando a riempire k registri ad L bit, la relazione tra i ritmi binari diviene ![]() .
.
9) Codifica differenziale :
È una codifica priva di ridondanza che si utilizza nel caso di codifica con memoria dove un errore si propaga determinando una sequenza binaria decodificata che dall´errore in poi è la negata di quella corretta. Il metodo in cui tale inconveniente viene eliminato consiste nella associare l´informazione non ai livelli bensì alla variazione degli stessi, ciò ad esempio si ottiene facendo si che se nella sequenza d´ingresso c´è uno 0 allora in quella d´uscita si mantiene il bit che c´era precedentemente mentre se nella sequenza d´ingresso c´è un uno allora nella sequenza d´uscita si inserisce il negato del bit che c´era precedentemente. In sede di decodificazione non si fa altro che comparare ogni cifra con la precedente.
10) Codifica con mutamento della cardinalità :
La sequenza y(n) d´ingresso va a riempire un registro a b bit dove b è funzione della cardinalità M della insieme M-nario secondo la ![]() ad ogni parola y viene associato un simbolo zq appartenente ad un insieme discreto.
ad ogni parola y viene associato un simbolo zq appartenente ad un insieme discreto.
Un tipico esempio è la codifica di Gray nella quale a parole binarie della sequenza d´ingresso che differiscano solo per un bit vengono associati elementi adiacenti della insieme dei simboli.
Modulazione a prodotto
11) Segnale modulato a prodotto :
Moltiplicando un segnale in banda base b(t) con una portante armonica ![]() si ottiene un segnale
si ottiene un segnale ![]() il cui spettro è
il cui spettro è ![]() costituito pertanto da due repliche dello spettro Pb(f) del processo in banda base traslate di ±fc e ridotte di ¼ .
costituito pertanto da due repliche dello spettro Pb(f) del processo in banda base traslate di ±fc e ridotte di ¼ .
La reversibilità si ottiene grazie ad un demodulatore nel quale il segnale sx(t) viene moltiplicato per un´oscillazione armonica 2c(t) prodotta da un oscillatore sincronizzato ottenendo ![]() dal quale si può riottenere il processo in banda base mediante un filtro passa basso con frequenza di taglio fc .
dal quale si può riottenere il processo in banda base mediante un filtro passa basso con frequenza di taglio fc .
12) Oscillatore reale :
L´oscillatore reale viene ottenuto mediante un amplificatore fatto lavorare in condizioni di instabilità mediante un circuito selettivo che determina il valore della pulsazione, l´oscillazione che ne deriva è :
![]()
dove aN(t) è la realizzazione di un processo denominato rumore d´ampiezza mentre jn(t) è la realizzazione di un processo denominato rumore di fase entrambe sono in valore assoluto molto minore di 1 mentre x(t) è la realizzazione di un processo denominato instabilità della oscillatore ed è dovuto a variazioni nel tempo degli elementi che condizionano la frequenza della oscillazione.
13) Oscillatori coerenti e non coerenti :
L´oscillazione prodotta da un oscillatore coerente presenta una instabilità pressoché costante nel tempo, la sua espressione è pertanto ![]() e risulta costituito da una frequenza fondamentale spostata rispetto ad f0 ed una densità spettrale di rumore che può essere filtrata via mediante un filtro passa-banda centrato su f0 . La stabilità può essere valutata mediante il rapporto
e risulta costituito da una frequenza fondamentale spostata rispetto ad f0 ed una densità spettrale di rumore che può essere filtrata via mediante un filtro passa-banda centrato su f0 . La stabilità può essere valutata mediante il rapporto ![]() che vale tipicamente 10-3 giungendo a 10-5 per oscillatori quarzati ed a 10-6 per oscillatori quarzati termostatati.
che vale tipicamente 10-3 giungendo a 10-5 per oscillatori quarzati ed a 10-6 per oscillatori quarzati termostatati.
Un oscillatore non coerente produce invece una oscillazione ![]() caratterizzata da una instabilità variabile nel tempo in maniera non trascurabile, è il caso della oscillazione prodotta da un LED o da un LASER.
caratterizzata da una instabilità variabile nel tempo in maniera non trascurabile, è il caso della oscillazione prodotta da un LED o da un LASER.
14) Descrivere la anello ad aggancio di fase :
Si ha un oscillatore libero ![]() del quale si può variare la frequenza agendo direttamente su una grandezza ai capi di un componente, esso può essere sincronizzato con una oscillazione coerente
del quale si può variare la frequenza agendo direttamente su una grandezza ai capi di un componente, esso può essere sincronizzato con una oscillazione coerente ![]() infatti effettuando il prodotto tra le due oscillazioni, e filtrando si ottiene un segnale proporzionale all´errore di fase e mediante un quadripolo QL si può variare
infatti effettuando il prodotto tra le due oscillazioni, e filtrando si ottiene un segnale proporzionale all´errore di fase e mediante un quadripolo QL si può variare ![]() in modo da agganciare i due oscillatori.
in modo da agganciare i due oscillatori.
