Segnali ed informazione
1) Segnale :
In senso stretto è una grandezza fisica, funzione reale di variabile reale utilizzabile o meno come veicolo per l´informazione.
2) Segnale certo :
È caratterizzato da un andamento noto ottenuto con funzioni matematiche, la sua rappresentazione grafica è denominata forma d´onda. Ad esso non è associata alcuna informazione in quanto tutti i parametri sono noti a priori.
3) Segnale aleatorio :
Si tratta di un segnale la cui forma non è nota a priori ed è invece legata alla informazione associata al segnale.
4) Segnale fedele ad x0(t) :
È un segnale che è traslato rispetto ad x0 ed è moltiplicato per una costante g ossia ![]() .
.
5) Condizioni di trasferimento corretto :
a) il generatore G è rappresentato con un generatore ideale ed una impedenza interna costante reale e positiva R
b) l´utilizzatore U è rappresentato con una impedenza costante reale e positiva Ru .
6) Condizioni di connessione ideale :
Deve essere massima la potenza istantanea p(t) scambiata, ciò si ottiene per Zg(f) = Zu(f) = R .
7) Segnale diretto e segnale riflesso :


8) Segnale scalare :
È un segnale avente un codominio monodimensionale.
9) Segnale regolare in to :
Esiste finito il limite ![]() .
.
10) Segnale continuo in t0 :
È un segnale per il quale si ha ![]() .
.
11) Segnale a tempo continuo :
Il dominio è un insieme continuo.
12) Segnale quantizzato uniformemente :
Un segnale si dice quantizzato uniformemente se i livelli di quantizzazione sono tutti equidistanziati.
13) Segnale impulsivo :
È un segnale che è nullo all´esterno di un intervallo di durata limitata.
14) Segnale impulsivo rettangolare :
Si estende da –T/2 a T/2 esso è ![]() .
.
15) Segnale impulsivo triangolare :
Si estende da –T/2 a T/2 esso è ![]() con
con  .
.
16) Segnale impulsivo a coseno rialzato :

17) Definire e fare un esempio di segnale bilatero :
È un segnale non nullo sia per tempi positivi che per tempi negativi, un esempio è  .
.
18) Definire e fare un esempio di segnale monolatero destro causale :
È non nullo solo per tempi positivi, un esempio è il segnale unilatero a decadenza esponenziale ![]() .
.
Si ha xMD(t) = x(t)u(t) .
19) Segnale monolatero sinistro anticausale :
È non nullo solo per tempi negativi , si ha xMS(t) = x(t)u(-t) .
20) Scomposizione di un segnale bilatero :
Se il segnale è reale, può essere scomposto nella somma della parte pari  e della parte dispari
e della parte dispari  mentre se è complesso può esser scomposto nella somma della parte hermitiana
mentre se è complesso può esser scomposto nella somma della parte hermitiana ![]() e della parte anti-hermitiana
e della parte anti-hermitiana ![]() .
.
21) Segnale a tempo discreto :
È definito solo negli istanti discreti {tn}.
22) Sequenza :
È un segnale a tempo discreto con istanti equispaziati x(tn) = x(nTc) , si ha ![]() .
.
23) Funzione generalizzata di Dirac :
È la d di Dirac definita dalla 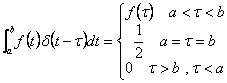
essa viene in genere approssimata come limite di funzioni continue.
