Variabili aleatorie
1) Variabili aleatorie :
Si tratta di una funzione che ha come dominio l´insieme S dei risultati di un esperimento e come codominio l´insieme dei numeri reali.
2) Funzione di distribuzione cumulativa :
Permette di quantificare la probabilità che la variabile aleatoria X assuma valori minori od uguali ad un dato valore x
3) Proprietà della funzione di distribuzione :
a) FX(-¥) = 0 FX(+¥) = 1
b) FX è una funzione monotona non decrescente, cioè se x1 £ x2 Û FX(x1) £ FX(x2)
c) P{X>x} = 1 - FX(x)
d) La funzione di distribuzione è continua da destra ![]()
e) P{x1 < X £ x2 } = FX(x2) - FX(x1)
f) il salto della funzione di distribuzione in corrispondenza di un punto di discontinuità x0 è uguale alla probabilità che la variabile assuma il valore x0
4) Variabile aleatoria di tipo continuo :
Una variabile aleatoria x si dice di tipo continuo se la sua funzione di distribuzione è continua.
5) Variabile aleatoria di tipo discreto :
Una variabile aleatoria x si dice di tipo discreto se la sua funzione di distribuzione è una funzione a gradini.
6) Variabile aleatoria di tipo misto :
Una variabile aleatoria x si dice di tipo misto se la sua funzione di distribuzione è discontinua ma non a gradini.
7) Distribuzione empirica :
Una distribuzione empirica è una funzione a gradini avente come punti del dominio i valori della variabile aleatoria corrispondente all´esito della prova, ad ognuno di essi la funzione empirica associa un gradino di altezza 1/n .
8) Percentile :
Il percentile u (o percentile n-esimo) della variabile aleatoria X è quel valore xu tale che P{X £ xu} = u. La funzione percentile è quindi l´inversa della funzione di distribuzione. In altre parole il 10 percentile indica il valore di x per il quale la area che va da -¥ ad x e sottesa dalla funzione di distribuzione è pari al 10% .
9) Mediana della variabile aleatoria X :
Si tratta del valore 0.5 percentile ed è indicato con la lettera m..
10) Funzione densità di probabilità :
La densità di probabilità fX(x) è definita come la derivata della funzione di distribuzione ![]() .
.
11) Proprietà della densità di probabilità :
a) La funzione di densità è non negativa fX(x) ³ 0
b) FX(x2) - FX(x1) = ![]()
c) FX(x) = ![]()
d) ![]()
e) P{ x1 < X £ x2 } = ![]()
12) Funzione di massa di probabilità per variabili aleatorie :
Si tratta della funzione pk = P { X = xk}.
13) Valore atteso :
Il valore atteso di una variabile aleatoria X è il centro di gravità della densità o delle masse di probabilità nei casi continuo o discreto rispettivamente. In altre parole è il valore medio della distribuzione.
14) Valore atteso di una variabile aleatoria continua :
![]()
15) Valore atteso di una variabile aleatoria discreta :
![]()
16) Proprietà della media statistica :
a) E[a*X] = a*E[X]
b) E[a*X + b*Y] = a*E[X] + b*E[Y]
17) Varianza :
La varianza di una variabile aleatoria X esprime una misura della “concentrazione” dei valori assunti da una variabile aleatoria attorno al suo valore medio.
![]()
18) Deviazione standard :
È la radice della varianza
![]()
19) Varianza di una variabile aleatoria continua :
![]()
20) Varianza di una variabile aleatoria discreta :
![]()
21) Relazione tra media quadratica e varianza :
![]()
22) Momento di ordine n di una variabile aleatoria X :
mn = E[Xn]
23) Momento centrale di ordine n di una variabile aleatoria X :
![]()
24) Disuguaglianza di Chebyschev :
![]()
25) Disuguaglianza di Markov :
![]()
26) Variabili statisticamente indipendenti :
Due variabili aleatorie X ed Y si dicono statisticamente indipendenti se, dati 2 insiemi arbitrari A e B di valori di X ed Y rispettivamente, si ha ![]() .
.
27) Variabile aleatoria uniforme :
Una variabile aleatoria continua X si dice uniforme tra ![]() e
e ![]() se la sua densità è costante nell´intervallo
se la sua densità è costante nell´intervallo ![]() e nulla altrove.
e nulla altrove.
28) Variabile aleatoria gaussiana :
Una variabile aleatoria continua X è detta gaussiana se la sua funzione di densità è della forma
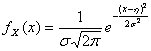
29) Variabile gaussiana standard :
Si tratta di una variabile gaussiana con valor medio nullo e varianza unitaria.
30) Funzione di densità di una variabile aleatoria esponenziale :
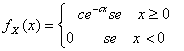
31) Funzione di densità di una variabile iperesponenziale :
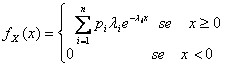
32) Funzione di densità di una variabile aleatoria distribuita secondo Rayleigh :
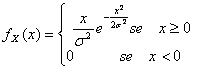
33) Funzione di densità di una variabile lognormale :
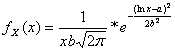
34) Funzione di densità di una variabile distribuita secondo il modello gamma :
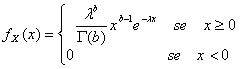
35) Funzione di densità di una variabile aleatoria distribuita secondo il modello chi-quadro :
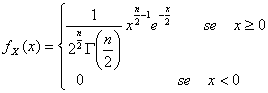
36) Funzione di densità di una variabile aleatoria distribuita secondo il modello di Erlang :

37) Funzione di densità di una variabile aleatoria distribuita secondo Student :
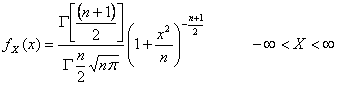
38) Funzione di densità di una variabile aleatoria distribuita secondo il modello K :
![]()
39) Funzione di densità di una variabile aleatoria distribuita secondo il modello beta :

40) Funzione di densità di una variabile aleatoria distribuita secondo il modello di Cauchy :
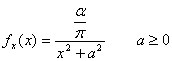
41) Funzione di densità di una variabile aleatoria distribuita secondo il modello binomiale :
![]()
42) Funzione di densità di una variabile aleatoria distribuita secondo il modello geometrico :
![]()
43) Variabile aleatoria Poissoniana :
Se l è un parametro ed X una variabile aleatoria intera e positiva.
![]()
44) Legge dei grandi numeri :
In una serie di n prove ripetute, in cui la probabilità di successo di una singola prova è pari a p, il rapporto tra il numero di successi k ed il numero di prove n tende a p quando n ® ¥ , ![]()
45) teorema centrale del limite per funzioni binomiali :
In una serie di n prove ripetute, indicando con X il numero di successi, si costruisce la variabile aleatoria Y
![]()
La distribuzione di probabilità FY(y) è tale che 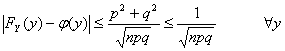
46) Funzione di distribuzione di una funzione di variabile aleatoria :
La funzione di distribuzione FY(y) fornisce la probabilità P{Y £ y}
47) Teorema fondamentale della densità di probabilità :
Per uno specifico valore y della densità fY(y) è data da 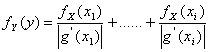
48) Valore atteso di una variabile aleatoria Y = g(X) :
![]()
