Teoremi sulle Equazioni differenziali ordinarie
Equazioni differenziali di 1° grado
1) Teorema delle contrazioni di Banach - Caccioppoli :
In uno spazio metrico completo una contrazione ammette sempre un unico punto fisso.
Esistenza :
preso un punto x0 arbitrario costruiremo una successione che converge ad un punto x~ : F(x~) = x~ .La successione è definita ricorsivamente come xn+1 = F(xn) . Sfruttando il fatto che F è contrazione si riesce a stabilire che
d(xn+1 , xn) £ rn d(x1 , x0) risultato che viene utilizzato per dimostrare che la successione è fondamentale in quanto di Cauchy datosi che d(xn , xm) £ e . Si ha infatti : ![]() da cui raccogliendo e sostituendo la somma della serie armonica si ottiene
da cui raccogliendo e sostituendo la somma della serie armonica si ottiene ![]() che tende a 0 per m®+¥ essendo 0 < r < 1 , pertanto la successione è di Cauchy e quindi converge.
che tende a 0 per m®+¥ essendo 0 < r < 1 , pertanto la successione è di Cauchy e quindi converge.
Supponiamo che converga a x~ allora sfruttando la continuità della contrazione F il limite della argomento può divenire il limite della funzione e quindi dimostrare che F(x~) = x~ .
Unicità :
Supponiamo che esistano 2 punti fissi, la distanza tra di essi sfruttando la definizione di contrazione, non può che essere 0, quindi i 2 punti in realtà sono lo stesso punto.
2) Condizione di Lipschitzianità per f :
Se f e la sua derivata parziale rispetto ad y sono continue in D Þ f è localmente lipschitziana rispetto ad y, uniformemente in t.
Si dimostra applicando il teorema del valor medio ![]()
3) Se la successione di funzioni continue fn converge uniformemente Þ il suo limite f è una funzione continua.
Si dimostra applicando il teorema dello scambio dei limiti alla funzione ![]() .
.
4) Lemma di Volterra :
Se j Î C1(Id) è soluzione del problema di Cauchy Þ j soddisfa l´equazione integrale di Volterra ![]() " t Î Id e viceversa.
" t Î Id e viceversa.
Þ E´ chiaro che se j è soluzione del problema di Cauchy Þ si può integrare la prima equazione del problema tra t e t e sostituire la condizione iniziale j(t) = x .
Ü Si ottiene derivando in quanto j è continua ed ha derivate continue in virtù della uguaglianza col 2° membro.
5) Teorema di esistenza e di unicità locale :
Sia f : D®Ân con D aperto di Ân+1 , continua in D e localmente lipschitziana in D, rispetto ad y ed uniformemente in t
Þ per ogni punto (t,x) Î D esiste un intorno Id di t tale che Id = [t-d , t+d] nel quale è definita una soluzione del problema di Cauchy. Tale soluzione è unica nel senso che ogni altra soluzione coincide con j nell´intervallo comune di definizione.
La dimostrazione è articolata nei tre seguenti passi :
a) Si associa al problema di Cauchy la corrispondente equazione di Volterra ![]()
b) Si individua uno spazio metrico completo
Uno spazio metrico completo è lo spazio delle funzioni continue su di un compatto, quindi " (t, x) Î D si individua un compatto G := { (t,y) Î Ân+1 : ||t-t|| < a e ||y-x||<b } , al suo interno individuiamo lo spazio metrico Y delle funzioni continue con grafico contenuto in G , Y := { j Î C(Id) : ||j(t)-x||<b } esso è uno spazio metrico completo a patto di adottare la metrica della convergenza uniforme d(j, y) = max || j(t) -y(t) ||
c) Si dimostra che il funzionale corrispondente alla equazione di Volterra è una contrazione e pertanto individua un unico punto fisso ossia un´unica soluzione.
All´equazione di Volterra si associa il funzionale ![]() , individuando ora delle restrizioni su d si è in grado di far vedere che si tratta di una contrazione :
, individuando ora delle restrizioni su d si è in grado di far vedere che si tratta di una contrazione :
a) Vogliamo che sia F[y] Ì Y Þ ![]() essendo M := max || f(t,y(t) || dobbiamo imporre Md < b e quindi d < b / M .
essendo M := max || f(t,y(t) || dobbiamo imporre Md < b e quindi d < b / M .
b) Vogliamo che sia contrazione ossia ![]() da cui sfruttando la locale lipschitzianità di f si ha :
da cui sfruttando la locale lipschitzianità di f si ha : ![]() dove l´ultima disuguaglianza è motivata dalla scelta della metrica della convergenza uniforme. Pertanto è una contrazione a patto che Ld < 1 Û d < 1 / L .
dove l´ultima disuguaglianza è motivata dalla scelta della metrica della convergenza uniforme. Pertanto è una contrazione a patto che Ld < 1 Û d < 1 / L .
Scegliendo d = min ( a , 1/L , b/M ) il teorema è dimostrato.
6) Condizione per l´esistenza di una soluzione massimale destra :
Sia f : D®Ân con D aperto di Ân+1 , continua in D e localmente lipschitziana in D, rispetto ad y ed uniformemente in t
Þ sia y :[t0 , b) ®Ân una soluzione massimale destra limitata Þ b = b
Dimostrare.
7) Lemma di Gronwall :
Siano I Ì Â un intervallo e t Î I. Siano inoltre u,v : I®Â due funzioni continue in I, non negative e c e Â+ .
Se ![]() " t Î I Þ
" t Î I Þ ![]() " tÎI .
" tÎI .
Sia ![]() supponendo t > t e moltiplicando per
supponendo t > t e moltiplicando per ![]() si ha
si ha ![]() in quanto la funzione a primo membro è decrescente avendo essa derivata negativa infatti :
in quanto la funzione a primo membro è decrescente avendo essa derivata negativa infatti : ![]() in quanto si ha v(t) £ w(t) e quindi w´(t) = u(t)v(t) £ u(t)w(t) . Dunque
in quanto si ha v(t) £ w(t) e quindi w´(t) = u(t)v(t) £ u(t)w(t) . Dunque ![]() pertanto
pertanto ![]() ..
..
8) Teorema di esistenza e di unicità globale :
Sia S := (t1 , t2) x Ân .Supponiamo che f sia definita in S e che in S f sia continua e localmente lipschitziana rispetto ad y ed uniformemente in t. Se inoltre esistono 2 costanti positive A e B tali che ||f(t,y)|| £ A + B||y|| " (t,y) Î S
Þ " (t,x) Î S , j(t ;t,x) è definita in t1 , t2 .
Per il teorema precedente ci basta dimostrare che la y(t) è limitata affinché l´intervallo sia massimale, a tal fine normando l´equazione integrale di Volterra ![]() si ha :
si ha :
![]() Pertanto y(t) è limitata e quindi ammette soluzione massimale.
Pertanto y(t) è limitata e quindi ammette soluzione massimale.
9) Teorema di esistenza e di unicità globale :
Sia f : (t1 , t2) x Ân ®Â una funzione continua e globalmente lipschitziana in Y con costante L Þ
Þ " (t,x) Î S , j(t ;t,x) è definita in t1 , t2 .
Dimostrare.
10) Teorema della dipendenza delle soluzioni dai dati iniziali :
Sia f :D®Ân continua e localmente lipschitziana rispetto ad y , uniformemente in t. Supponiamo inoltre che nell´intorno del punto (t0, x0) vi siano punti in cui ogni soluzione è definita in un intervallo comune a tutte inoltre se (t ,x) ®(t0 ,x0 ) Þ j(t ;t,x)®j(t ; t0 , x0)
Metodi di risoluzione di equazioni differenziali del 1° ordine
11) Formula risolutiva delle equazioni differenziali lineari :
Sono equazioni nella forma ![]() , l´integrale generale è dato dalla formula :
, l´integrale generale è dato dalla formula :
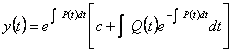
12) Formula risolutiva delle equazioni differenziali esatte :
Sono equazioni nella forma ![]() , l´integrale generale è dato dalla formula :
, l´integrale generale è dato dalla formula :
![]()
essendo F(t,y) una funzione potenziale
13) Equazioni a variabili separabili :
Sono equazioni nella forma ![]() , l´integrale generale è dato dalla formula :
, l´integrale generale è dato dalla formula :
![]()
14) Equazioni di Bernoulli :
Sono equazioni nella forma ![]() , si risolvono dividendo per ya e risolvendo la risultante equazione differenziale lineare del 1° ordine.
, si risolvono dividendo per ya e risolvendo la risultante equazione differenziale lineare del 1° ordine.
15) Equazioni omogenee o di Manfredi :
Sono equazioni nella forma ![]() , si risolvono ponendo
, si risolvono ponendo ![]() e risolvendo la risultante equazione differenziale a variabili separabili.
e risolvendo la risultante equazione differenziale a variabili separabili.
16) Come risolvere equazioni del tipo y = F(x , y´) :
Si deve porre y´ = p quindi derivare rispetto ad x , sostituendo quindi p´ = dp/dx si ottiene una equazione a variabili separabili risolvendo la quale si ricavano x ed y in funzione di p
17) Equazioni di D´Alembert - Lagrange :
Si tratta di equazioni nella forma y = x g(y´) + f(y´) , si risolve ponendo y´ = p quindi derivare rispetto ad x , Si riporta quindi ad una equazione lineare in funzione della x risolvendo la quale si ottiene una soluzione parametrica di x ed y in funzione di c.
Equazioni differenziali di ordine n
18) Criterio base per la trattazione :
Ogni equazione differenziale di ordine n può essere ricondotta ad un sistema lineare di n equazioni del 1° ordine pertanto per dimostrare l´esistenza e l´unicità della soluzione, si può far ricorso a quanto già dimostrato per le equazioni differenziali del 1° ordine e valido anche per i sistemi lineari a patto di cambiare il simbolismo.
19) Condizione necessaria e sufficiente perché n soluzioni della equazione siano linearmente indipendenti :
Il determinante della matrice wronskiana deve essere 0  ¹ 0
¹ 0
20) Teorema di Liouville :
Il wronskiano di una equazione differenziale di ordine n soddisfa la ![]()
Dimostrare
21) Teorema di Lagrange :
Siano y1 , ... , yn n soluzioni indipendenti della omogenea, Þ una soluzione della non - omogenea è fornita dalla formula
![]()
22) Teorema di sovrapposizione :
Se b(t) = b1(t) + b2(t) e conosciamo un integrale particolare della equazione con termine noto b1(t) ed uno della equazione con termine noto b2(t) Þ La somma dei 2 integrali sarè un integrale della equazione con termine noto b(t)
Sistemi di equazioni differenziali del 1° ordine
23) Criterio base per la trattazione :
I criteri di esistenza ed unicità locale e globale sono i medesimi ad eccezione della notazione.
24) Condizione necessaria e sufficiente perché n soluzioni della equazione siano linearmente indipendenti :
Non deve essere nullo il determinante della matrice wronskiana 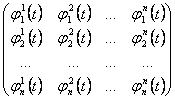
25) Teorema di Liouville :
Il wronskiano di un sistema di soluzioni della equazione ![]() soddisfa l´equazione differenziale
soddisfa l´equazione differenziale ![]() dove a(t) è la traccia della matrice A(t).
dove a(t) è la traccia della matrice A(t).
26) Corollario del teorema di Liouville :
Il wronskiano di una equazione differenziale di ordine n soddisfa la ![]() dove a(t) è la traccia della matrice rappresentativa
dove a(t) è la traccia della matrice rappresentativa
27) Metodo di variazione delle costanti arbitrarie (Teorema di Lagrange) :
Per ottenere la soluzione generale del sistema non omogeneo ![]() è sufficiente aggiungere alla soluzione generale del corrispondente sistema omogeneo
è sufficiente aggiungere alla soluzione generale del corrispondente sistema omogeneo ![]() una soluzione particolare ricavabile ad esempio tramite la formula :
una soluzione particolare ricavabile ad esempio tramite la formula : ![]()
