Geometria del piano
1) Equazioni che descrivono le rette nel piano:
Le rette nel piano possono essere descritte in 2 modi diversi:
Equazione cartesiana esplicita
Si tratta della forma ax1 + bx2 = c dove:
x1 = ascissa di un qualsiasi punto della retta
x2 = ordinata associata ad x1 per quella retta
c = ordinata all´origine
Da questa si passa agevolmente alla forma esplicita dove ![]()
dove -b/a = m viene definito coefficiente angolare in quanto se si suppone la retta passante per l´origine si nota che x2/x1 è un rapporto costante caratteristico per quella retta, mentre se si prende una qualsiasi altra retta, tale rapporto varia ma continuerà ad essere costante per quella retta.
2) Rette parallele:
In base a quanto appena detto riesce intuitivo pensare che 2 rette siano parallele quando differiscano soltanto per la coordinata all´origine c , mentre il rapporto -b/a rimane immutato.
3) Rette ortogonali:
Una retta r2 è ortogonale alla retta r1 quando con essa forma un angolo di 90°.
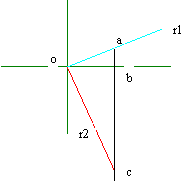 |
Osservando il disegno se si pone ob =1 allora m1= oa / ob = oa ed anche m2 = oc / ob = oc. Ma Euclide ci dice che se il triangolo è rettangolo allora ab * bc = 12 Þ | m1 * m2 | =1 da cui segue che il coefficiente angolare di una retta è pari all´inverso del coefficiente angolare della retta ad essa ortogonale e di segno opposto visto che sicuramente cade in un altro quadrante del piano. Ad esempio:
r1 Þ 5x1 + 2x2 = 2 m = -5/2
è ortogonale alla retta
r2 Þ 5x1 - 2x2 = c m = 2/5
Più in generale, è stata fonte di confusione e continuerà ad esserlo, possiamo descrivere un vettore v^ ortogonale alla retta r1 e passante per l´origine tale che : v^ = ![]()
ed un vettore v// parallelo alla retta : v// = ![]()
Tutto ciò deriva dalla osservazione che se prendiamo 2 punti sulla retta r1 , x ed y allora la loro differenza è un vettore parallelo alla retta r1 applicato nella origine. Se di questo vettore (x - y) facciamo il prodotto scalare con v^ otteniamo 0 e pertanto i 2 vettori sono tra di loro ortogonali. Se invece facciamo il prodotto scalare con il vettore v// otteniamo il modulo di (x-y) pertanto i 2 vettori sono paralleli.
** Ricordiamo infatti che il prodotto scalare di 2 vettori non è che la proiezione ortogonale di uno dei 2 sulla retta dove giace la altro; tale proiezione non è un vettore bensì un numero ed è individuato dal prodotto delle norme dei 2 vettori per la angolo tra essi sotteso.
3) Equazione parametrica:
Si tratta della forma ![]() =
= ![]()
![]() + t
+ t![]() dove:
dove:
![]() = coordinate del generico punto della retta
= coordinate del generico punto della retta
![]() = coordinate di un punto qualsiasi sulla retta
= coordinate di un punto qualsiasi sulla retta
![]() = coordinate di un vettore parallelo alla retta cercata ed applicato nella origine del piano
= coordinate di un vettore parallelo alla retta cercata ed applicato nella origine del piano
t = parametro alcui variare siamo in grado di far assumere ad ![]() il valore di tutti i punti sulla retta.
il valore di tutti i punti sulla retta.
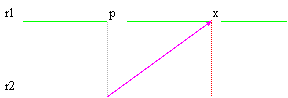
In pratica questa form a si basa sulla osservazione che una retta può essere descritta avendo a disposizione un punto per la quale essa passa ed un vettore ad essa parallelo passante per l´origine del piano.
 |
![]()
Da questa figura si nota agevolmente che il generico punto x si trova semplicemente eseguendo la somma vettoriale tra il vettore v moltiplicato per un parametro t ed il vettore op , vien da se che al variare di (t * v) siamo in grado di descrivere qualsiasi punto x sulla retta r1 .
3) Rette parallele con l'equazione parametrica:
In base a quanto appena detto riesce intuitivo pensare che 2 rette siano parallele quando hanno lo stesso vettore direttore v o uno ad esso proporzionale. Ad esempio:
r1 = ![]()
![]() + t
+ t![]() è parallela alla retta r2 =
è parallela alla retta r2 = ![]()
![]() + t
+ t![]()
4) Rette ortogonali con l'equazione parametrica:
Una retta r2 è ortogonale alla retta r1 quando con essa forma un angolo di 90°.
Anche qui vale la stessa osservazione fatta per l´equazione cartesiana, in particolare dobbiamo individuare un vettore v1 che sia ortogonale al vettore v2
 |
Torna a valere quanto affermato precedentemente ossia una retta r2 per essere otogonale ad r1 deve avere le coordinate del vettore direttore v2 pari all´inverso delle coordinate del vettore direttore v1 e ordinata di segno opposto visto che sicuramente cade in un altro quadrante del piano.
Ad esempio:
r1 = ![]()
![]() + t
+ t![]() è ortogonale alla retta r2 =
è ortogonale alla retta r2 = ![]()
![]() + t
+ t![]()
5) Problemi risolvibili agevolmente con l´equazione parametrica :
a) Retta passante per 2 punti distinti p1 e p2
Per identificare una retta con l´equazione parametrica ci occorrono:
1 punto Þ possiamo prendere uno dei 2 ad esempio p1
1 vettore passante per l´origine e parallelo alla retta Þ possiamo prendere il vettore differenza ossia p1 - p2
Abbiamo così individuato l´equazione parametrica della retta che al variare di t descrive tutti i punti della retta stessa. Ad esempio siano p1 = ![]() e p1 =
e p1 = ![]() allora il vettore v vale
allora il vettore v vale ![]() -
- ![]() =
=![]() = v
= v
pertanto l´equazione parametrica completa risulta essere : ![]() =
= ![]()
![]() + t
+ t![]()
b) Data una retta r1 ed un punto p ad essa esterno trovare l´equazione della retta passante per p ortogonale ad r1
Si risolve al solito considerando che ci occorrono:
punto Þ possiamo prendere p
1 vettore passante per l´origine e parallelo alla retta Þ il vettore lo prendiamo direttamente ortogonale alla retta data utilizzando quanto già dimostrato.
pertanto se sono dati: p = ![]() e
e ![]() =
=![]()
![]() + t
+ t![]()
allora l´equazione della retta ortogonale cercata vale : ![]() =
=![]()
![]() + t
+ t![]() .
.
c) Intersezione tra 2 rette r1 e r2 di equazione parametrica data
Si ottiene agevolmente imponendo che il punto generico ![]() appartenga ad entrambe le rette, questo dà luogo ad un sistema composto da 2 equazioni nelle incognite t ed s dalle quali si possono dedurre questi 2 parametri, sostituendo poi o s oppure t nella rispettiva equazione dobbiamo trovare lo stesso punto ricercato rappresentante l´intersezione delle 2 rette. Sono possibili le seguenti eventualità:
appartenga ad entrambe le rette, questo dà luogo ad un sistema composto da 2 equazioni nelle incognite t ed s dalle quali si possono dedurre questi 2 parametri, sostituendo poi o s oppure t nella rispettiva equazione dobbiamo trovare lo stesso punto ricercato rappresentante l´intersezione delle 2 rette. Sono possibili le seguenti eventualità:
c1) Nessuna soluzione se le due rette sono parallele
c2) Una coppia di valori (x1 , x2) se le due rette si intersecano in un solo punto
c3) Infinite soluzioni se le rette sono coincidenti, questo accade ad esempio quando uno dei 2 parametri è libero
Ad esempio:
![]() =
=![]()
![]() + t
+ t![]() e
e ![]() =
= ![]()
![]() + s
+ s![]()
i punti generici sono:
![]() e
e ![]()
da cui :
![]() =
= ![]()
![]() le cui soluzioni sono : t = 0 e s = 0
le cui soluzioni sono : t = 0 e s = 0
pertanto il punto di incontro è p = ![]() .
.
c4) Dati una retta r1 ed un punto p calcolare la distanza di p rispetto ad r1
Si ottiene quale elaborazione dei precedenti in 2 passi successivi:
a) si calcola la equazione della retta ortogonale ad r1 passante per p
b) si trova il punto q d´intersezione tra le 2 rette
c) si calcola la distanza di p da q tramite il teorema di Pitagora ossia :
![]()
6) Passaggio da una equazione cartesiana alla corrispondente equazione parametrica:
Si trovano 2 punti sulla retta e poi si applica la algoritmo 1 per la ricerca della equazione parametrica della retta passante per 2 punti.
7) Passaggio da una equazione parametrica alla corrispondente equazione cartesiana:
Si prendono le 2 coordinate del punto generico espresse dalla equazione parametrica e si isola t in entrambe dopodichè uguagliandole si toglie t e rimane una equazione in x1 e x2 , quella è l´equazione cartesiana della retta .
8) L´equazione cartesiana per la risoluzione di problemi tipici:
a) Retta passante per 2 punti distinti p1 e p2
Si calcola a partire dalle coordinate dei punti: p1 = ![]() e p2 =
e p2 = ![]()
realizzando la differenza delle coordinate riferite alla equazione cartesiana ax1 + bx2 = c
b) Intersezione tra 2 rette
Si ottiene agevolmente mettendo a sistema le equazioni in forma esplicita , e risolvendo il sistema ad esempio con il metodo di Gauss riducendolo ad una matrice, la soluzione sarà la seguente:
b1) Nessuna soluzione se le due rette sono parallele
b2) Una coppia di valori (x1 , x2) se le due rette si intersecano in un solo punto
b3) Infinite soluzioni se le rette sono coincidenti, questo accade ad esempio quando una delle 2 incognite è libera
c) Dati una retta r1 ed un punto p calcolare la distanza di p rispetto ad r1
Si ottiene quale elaborazione dei precedenti in 2 passi successivi:
c1) avendo l´equazione cartesiana della retta r1 Þ ax1 + bx2 = c si passa alla corrispondente equazione parametrica della retta perpendicolare ricordando che :
un vettore v^ ortogonale alla retta r1 e passante per l´origine tale che : v^ = ![]()
pertanto l´equazione è: ![]() =
= ![]()
![]() + t
+ t![]()
c2) si trova il punto q d´intersezione tra le 2 rette ed il valore del corrispondente parametro t
c3) si calcola la distanza di p da q tramite il teorema di Pitagora ossia :
![]()
