Serie di Fourier
1) Definizione di funzione periodica x(t) :
E' una funzione x(t) per la quale si ha ![]() con k = 0, ±1, ±2 .
con k = 0, ±1, ±2 . ![]() .
.
2) Serie di Fourier di una funzione periodica x(t) di periodo T :
Se la funzione x() è integrabile in modulo ossia se ![]() allora è possibile definire una serie di Fourier ad essa associata
allora è possibile definire una serie di Fourier ad essa associata ![]() essendo i coefficienti di Fourier:
essendo i coefficienti di Fourier:
![]() e
e ![]() con k=0,1,2 . ∞
con k=0,1,2 . ∞
3) Ortogonalità delle funzioni ![]() e
e ![]() :
:
![]() essendo
essendo ![]()
4) Condizione di convergenza e quindi di esistenza della serie di Fourier :
La serie esiste a patto che x(t) sia limitata nell'intervallo [0,T] e converge ad x(t) in tutti i punti di continuità mentre converge ad ![]() in ogni punto di discontinuità.
in ogni punto di discontinuità.
5) Formula di Eulero :
![]()
inoltre si ha :
![]() e
e ![]()
6) Forma esponenziale complessa della serie di Fourier :
![]() essendo
essendo ![]() con k = -
con k = -![]() , . , +
, . , +![]()
La relazione con i coefficienti di Fourier è:
![]()
![]()
![]()
7) Coefficienti di Fourier nel caso di x(t) reale :
I coefficienti ak e bk sono reali mentre i ck sono hermitiani ossia ![]() .
.
8) Coefficienti di Fourier nel caso di x(t) reale e simmetrica:
I coefficienti ak sono reali, i bk sono tutti nulli mentre i ck sono reali e simmetrici ossia ![]() .
.
9) Spettro di ampiezza e spettro di fase di un segnale periodico x(t) :
Si considerano i coefficienti della serie di Fourier scritti in forma esponenziale complessa, lo spettro di ampiezza rappresenta i moduli dei coefficienti al variare di k da -![]() a +
a +![]() mentre lo spettro di fase rappresenta le fasi dei coefficienti al variare di k da -
mentre lo spettro di fase rappresenta le fasi dei coefficienti al variare di k da -![]() a +
a +![]() .
.
10) Teorema di Parseval per segnali periodici :
Per un segnale periodico in un periodo T la sua energia mediata su di un periodo vale![]() dove
dove ![]() rappresenta la potenza media della armonica di ordine k.
rappresenta la potenza media della armonica di ordine k.
11) Coefficienti di Fourier di una serie di impulsi :
![]()
12) Analizzatore di spettro per segnali periodici :

Si deduce in maniera semplice osservando che ![]() e che si ha
e che si ha ![]() e
e ![]() .
.
13) Derivata della serie di Fourier :
![]() essendo
essendo ![]()
14) Trasformata di Fourier del segnale x(t) :
![]()
Condizione sufficiente per l'esistenza della trasformata è l'assoluta sommabilità di x(t) ossia ![]() in particolare i segnali di energia sono anche assolutamente sommabili e pertanto ammettono trasformata di Fourier.
in particolare i segnali di energia sono anche assolutamente sommabili e pertanto ammettono trasformata di Fourier.
15) Funzione Kernel :
![]()
16) Trasformata di Fourier inversa :
![]()
17) Convoluzione di due funzioni f(t) ed h(t) :
![]()
18) Trasformata di Fourier di una convoluzione di due funzioni x(t) ed y(t) :
![]()
19) Oscillazioni di Gibbs :
Se la funzione x(t) è discontinua in t0 allora si avranno delle oscillazioni di Gibbs nella forma ricostruita tramite la trasformata inversa di Fourier, l'ampiezza delle oscillazioni si riduce allargando l'intervallo di integrazione.
20) Casi in cui viene impiegata la Trasformata di Fourier :
- Segnali ad energia finita come un impulso rettangolare, si ottiene lo spettro di energia
- Segnali a potenza finita come un segnale periodico o una successione di impulsi infiniti, si ottiene lo spettro di potenza
21) Teorema di Parseval per segnali di energia :
![]()
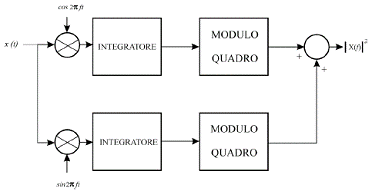
dove ![]() è la densità spettrale di energia e si calcola con il seguente schema:
è la densità spettrale di energia e si calcola con il seguente schema:
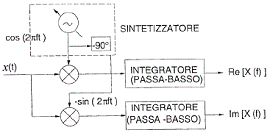
22) Schema per ottenere parte reale ed immaginaria della trasformata di Fourier per funzioni tempo-continue, aperiodiche e reali :
23) Proprietà di linearità della trasformata di Fourier :
![]()
24) Proprietà di dualità della trasformata di Fourier :
![]()
25) Proprietà di scalatura della trasformata di Fourier :
![]()
26) Proprietà di coniugio della trasformata di Fourier :
![]()
27) Proprietà di derivazione dell'integrale di Fourier :
![]()
28) Proprietà di integrazione dell'integrale di Fourier :
![]()
