Elementi di meccanica quantistica

1)       Equazioni di Hamilton - Jacobi :

                                       

sono equazioni in grado di descrivere completamente l´evoluzione temporale di un sistema di cui sia nota l´hamiltoniana.

 

2)       Confronto tra le onde ed i sistemi classici di particelle :

Posizione, velocità ed energia di una particella classica possono essere definite con precisione infinita mentre per un´onda  se è noto il k non è noto x e viceversa.

 

3)       Cause della crisi della meccanica classica :

I seguenti effetti non trovano spiegazione con la meccanica classica :

Spettro di emissione del corpo nero

La teoria classica di Rayleigh e Jeans ha determinato che per l®0 la energia emessa dal corpo nero tende ad infinito, mentre nella realtà sperimentale tende a 0, l´ipotesi di Planck è che lo scambio di energia tra le pareti del corpo nero e la radiazione avvenga in forma quantizzata multipli di un quanto E₀= hn .

Effetto fotoelettrico

Si tratta della emissione di elettroni da parte di un solido investito da un fascio di luce, sperimentalmente si ha che se la frequenza del fotone incidente è minore di un minimo non si estrae nessun elettrone indipendentemente dal numero di fotoni incidenti mentre se la frequenza è maggiore basta anche un solo fotone per estrarre un elettrone ed il numero è proporzionale al numero dei fotoni incidenti. La spiegazione venne fornita da Einstein il quale ipotizzò che l´onda elettromagnetica ceda agli elettroni energia in multipli di un quanto elementare E₀=hn .

Modello atomico di Bohr

Lo spettro di emissione di un atomo risulta caratterizzato da righe ben distinte, il motivo di ciò è stato trovato nel modello di Bohr il quale prevede che gli elettroni possano ruotare intorno al nucleo soltanto su orbite stazionarie ben definite dalla quantizzazione del momento angolare e che su tali orbite gli elettroni non emettono radiazione.

 

4)       Lunghezza d´onda di De Broglie :

è una relazione importante in quanto lega una grandezza corpuscolare ad una grandezza ondulatoria.

 

5) Equazione di Schroedinger :

 

6) Principio di corrispondenza :

                                                

 

7) Equazione di continuità :

 

8) Prodotto scalare di funzioni d´onda :

 

9) Valore atteso di un osservabile :

nel caso di operatori hermitiani si ha che il valore atteso è una grandezza reale.

 

10) Soluzione della equazione di Schroedinger nel caso di potenziale indipendente dal tempo :

È possibile scomporre il potenziale nel prodotto f(r,t) = T(t) u(r) che per la parte dipendente dal tempo ha soluzione  mentre la parte dipendente dal tempo da luogo all´equazione agli autovalori  che ha soluzione generale .

 

11) Principio d´indeterminazione :

è un principio che deriva dalla non commutatività tra l´operatore posizione e l´operatore quantità di moto.

 

12) Funzione d´onda della particella libera :

Si tratta di un´onda piana  e l´elettrone ha quantità di moto  .

 

13) Funzione d´onda della particella in una buca di potenziale a pareti infinite :

Assumendo il potenziale nullo tra –a ed a ed ¥ all´esterno, si ha che i livelli di energia concessi assumono valori  e la funzione d´onda per n dispari vale  mentre per n pari vale  .

 

14) Funzione d´onda della particella in una buca di potenziale a pareti finite :

Assumendo il potenziale nullo tra –a ed a ed U₀ all´esterno, si trova che i livelli energetici son quelli che soddisfano le equazioni trascendenti per soluzioni pari e  per soluzioni dispari essendo   e  .

 

15) Energie quantizzate nel caso di un oscillatore armonico :

I livelli energetici permessi sono  pertanto si ha una energia minima non nulla per n = 0  ed i livelli quantici sono distanziati tra loro di multipli di .

 

16) Probabilità di Tunneling :

La probabilità di Tunneling diminuisce esponenzialmente alla aumentare della larghezza  d della barriera ossia .

 

17) Densità di stati nei casi tridimensionale, bidimensionale, monodimensionale :

Nel caso della particella libera 3D si ha  , per la particella in una buca di potenziale a pareti infinite ossia libera 2D si ha  mentre per il filo quantico ossia la particella libera 1D si ha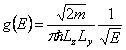

 

18) Funzione di distribuzione per particella classica, fermione, bosone :

La funzione di distribuzione f(E) rappresenta la probabilità che lo stato ad energia E ha di essere occupato, per una particella classica si ha la distribuzione di Maxwell-Boltzmann , per i fermioni caratterizzati da spin semintero invece si ha la distribuzione di Fermi-Dirac 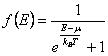 ed infine per i bosoni aventi spin intero si ha la funzione di distribuzione di Bose-Einstein  .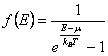