Caratterizzazione dei circuiti e stima delle prestazioni
1) Stima della resistenza :
La resistenza presentata da uno strato di materiale conduttore è  dove Rs è la resistenza del foglio e si misura in W/ . Tali resistenze nel caso del polisilicio e delle diffusioni sono influenzate dalla concentrazioni di droganti e dalla presenza di materiali come i silicidi.
dove Rs è la resistenza del foglio e si misura in W/ . Tali resistenze nel caso del polisilicio e delle diffusioni sono influenzate dalla concentrazioni di droganti e dalla presenza di materiali come i silicidi.
Un dispositivo MOS inoltre può essere spesso caratterizzato dalla sua resistenza ![]() .
.
2) Condensatore CMOS :
Il condensatore CMOS è formato esclusivamente da substrato p-doped, SiO2 e gate metallico o in polisilicio, si possono presentare le seguenti situazioni :
a) accumulazione : al gate viene applicata una tensione negativa, essa attrae le lacune verso l´ossido pertanto la capacità è soltanto quella della ossido  con A = area del gate e eSiO2 =3.9 .
con A = area del gate e eSiO2 =3.9 .
 b) depletion : una tensione debolmente positiva allontana le lacune ma non è in grado di attrarre gli elettroni, ne deriva che nei pressi della ossido si ha uno strato svuotato di portatori ampio d ed avente capacità
b) depletion : una tensione debolmente positiva allontana le lacune ma non è in grado di attrarre gli elettroni, ne deriva che nei pressi della ossido si ha uno strato svuotato di portatori ampio d ed avente capacità  con eSi = 12 .
con eSi = 12 . ![]() è pertanto la capacità complessiva presentata dal condensatore MOS , serie di C0 e di Cdep
è pertanto la capacità complessiva presentata dal condensatore MOS , serie di C0 e di Cdep
c) inversione : una tensione positiva superiore alla Vt richiama elettroni dal substrato i quali vengono a costituire un canale, tali elettroni però non riescono a seguire variazioni del segnale d´ingresso a frequenze superiori a 100Hz pertanto per frequenze inferiori la capacità è C0 mentre per frequenze superiori occorrerà considerare anche la capacità Cdep e quindi la capacità complessiva è Cgb che è anche la minima possibile.
3) Capacità di gate di un MOS :
 Le capacità parassite presenti in un MOS sono rappresentate dalla seguente figura
Le capacità parassite presenti in un MOS sono rappresentate dalla seguente figura
In particolare la capacità del gate è Cg = Cgb + Cgs + Cgd dove Cgs e Cgd sono intese tra il gate ed il canale quindi se quest´ultimo è assente sono assenti anche esse pertanto a seconda della regione di funzionamento del MOS si ha:
a) interdizione : il canale è assente quindi l´unica capacità è Cgb data dalla serie di C0 e Cdep
b) non-saturazione : il canale è formato pertanto Cgb = 0 mentre ![]()
c) saturazione : il canale non è formato dal lato del drain quindi Cgd = 0 mentre ![]()
Al fine di calcolare i ritardi nei circuiti digitali si può approssimare Cg = C0 .
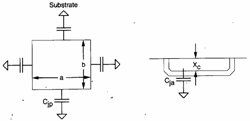 Per quanto riguarda invece le capacità Cdb e Csb presentate verso il substrato dalle diffusioni di source e drain , si ha che ciascuna di essa vale
Per quanto riguarda invece le capacità Cdb e Csb presentate verso il substrato dalle diffusioni di source e drain , si ha che ciascuna di essa vale ![]() dove Cja è la capacità in verticale tra la diffusione ed il substrato mentre Cjp è la capacità periferica presentata dai 4 lati della diffusione la quale ha una profondità non nulla.
dove Cja è la capacità in verticale tra la diffusione ed il substrato mentre Cjp è la capacità periferica presentata dai 4 lati della diffusione la quale ha una profondità non nulla.
Sia Cja che Cjp sono però funzione della tensione presente ai capi della giunzione secondo la  dove Cj0 è la capacità nel caso la tensione ai capi della giunzione sia nulla, Vb @ 0.6V ed m varia da 0.3 a 0.5 a seconda della discontinuità della giunzione.
dove Cj0 è la capacità nel caso la tensione ai capi della giunzione sia nulla, Vb @ 0.6V ed m varia da 0.3 a 0.5 a seconda della discontinuità della giunzione.
4) Analisi e soluzioni per circuiti RC distribuiti :
Nel caso di connessioni in polisilicio molto lunghe oppure connessioni in metallo pesantemente caricate, si hanno dei forti ritardi di propagazione che possono essere studiati mediante la teoria delle linee pensando la linea suddivisa in infinite tratte aventi spessore infinitesimo, resistenza ad unità di lunghezza r e capacità ad unità di lunghezza c, si deriva che il ritardo tx subito da un segnale che attraversa un percorso lungo x è ![]() . Un´analisi discreta porta invece a calcolare il ritardo tn dovuto alla sezione n-esima , si ha
. Un´analisi discreta porta invece a calcolare il ritardo tn dovuto alla sezione n-esima , si ha  .
.
L´andamento quadratico del ritardo rispetto alla distanza è molto pesante, tanto da rendere consigliabile in alcuni casi inserire dei buffer lungo la linea i quali rigenerino il segnale, il ritardo che si ottiene anche considerando un ritardo interno al buffer di alcuni ns , è sempre inferiore al ritardo che si ha in assenza del buffer. Alternativamente si può disporre la sorgente nel chip in modo che disti poco dal destinatario, questo è il motivo per il quale il clock sovente si trova al centro del chip. Un modello per il calcolo del ritardo è :
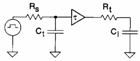
5) Tempi caratteristici riguardanti la commutazione di una porta :
tr tempo necessario affinché l´uscita passi dal 10% al 90% del suo valore stazionario
tf tempo necessario affinché l´uscita passi dal 90% al 10% del suo valore stazionario
td tempo che intercorre tra la variazione del 50% della ingresso e la variazione del 50% della uscita , vengono anche definiti i tempi tdr e tdf relativi alla crescita e alla discesa
6) Modello analitico di ritardo di un inverter CMOS :

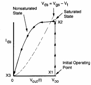 Vengono calcolati i tr e tf per il seguente circuito quando sia ad esso applicata un´onda quadra con fronti a pendenza infinita. Per il calcolo del tempo di discesa, facciamo riferimento all´nMOS . Se in ingresso c´è uno 0 allora l´nMOS è interdetto (X1) e l´uscita sarà al valore massimo VDD . Quando l´ingresso passa ad 1 , l´nMOS istantaneamente passa in saturazione (X2) ed inizia a scaricarsi secondo una rampa, ma quando arriva a Vout = VDD – Vtn passa in saturazione e si scarica con legge quadratica sino a VSS (X3).
Vengono calcolati i tr e tf per il seguente circuito quando sia ad esso applicata un´onda quadra con fronti a pendenza infinita. Per il calcolo del tempo di discesa, facciamo riferimento all´nMOS . Se in ingresso c´è uno 0 allora l´nMOS è interdetto (X1) e l´uscita sarà al valore massimo VDD . Quando l´ingresso passa ad 1 , l´nMOS istantaneamente passa in saturazione (X2) ed inizia a scaricarsi secondo una rampa, ma quando arriva a Vout = VDD – Vtn passa in saturazione e si scarica con legge quadratica sino a VSS (X3).
Evidentemente quindi il calcolo del tempo di discesa si suddivide in due fasi, una nella quale l´nMOS è in saturazione (…Si risolve per separazione delle variabili l´equazione ![]() , integrando tra 0.9VDD e VDD-Vtn si ottiene
, integrando tra 0.9VDD e VDD-Vtn si ottiene ![]() … ) e la altra nella quale è in regione di triodo
… ) e la altra nella quale è in regione di triodo
(…con l´espressione della IDS per la regione di triodo ed integrando tra VDD – Vtn e 0.1VDD si ottiene ![]() … ) . La somma dei due tempi può essere approssimata al valore
… ) . La somma dei due tempi può essere approssimata al valore  con k compreso tra 3 e 4 ed in maniera analoga si ottiene per il tempo di salita
con k compreso tra 3 e 4 ed in maniera analoga si ottiene per il tempo di salita  , ciò implica che se i MOS hanno le stesse dimensioni, il tempo di salita è il doppio del tempo di discesa in quanto la mobilità degli elettroni è doppia rispetto alla mobilità delle lacune, per avere gli stessi tempi occorre fare Wp = 2 Wn .
, ciò implica che se i MOS hanno le stesse dimensioni, il tempo di salita è il doppio del tempo di discesa in quanto la mobilità degli elettroni è doppia rispetto alla mobilità delle lacune, per avere gli stessi tempi occorre fare Wp = 2 Wn .
Per quanto riguarda i tempi di ritardo essi sono semplicemente la metà dei rispettivi tempi di salita o di discesa e possono essere espressi nella forma ![]() e
e ![]() dove Ap ed An hanno una espressione complessa ma possono essere approssimati al valore 0.36 calcolato con SPICE .
dove Ap ed An hanno una espressione complessa ma possono essere approssimati al valore 0.36 calcolato con SPICE .
7) Ritardo di una porta logica :
Il ritardo di una porta logica semplice può essere calcolato costruendo un inverter equivalente nel quale cioè le dimensioni del pull-down e quelle del pull-up riflettano i percorsi che effettivamente sono attivi nel pull-down e nel
 pull-up , in particolare considerando ad esempio una nand a 3 ingressi
pull-up , in particolare considerando ad esempio una nand a 3 ingressi
si ha che per il pull-down occorre considerare la serie dei 3 nMOS e quindi delle loro conduttanze quindi per bn1 = bn2 = bn3 si ha ![]() mentre per il pull-up occorre considerare solo 1 pMOS quindi
mentre per il pull-up occorre considerare solo 1 pMOS quindi ![]() in definitiva considerando
in definitiva considerando ![]() e
e ![]() si ha tr @ tf . Questa metodologia può essere motivata immaginando di far tendere a 0 la distanza tra i gate dei 3 nMOS, si ha infatti in tal caso un unico gate largo 3L.
si ha tr @ tf . Questa metodologia può essere motivata immaginando di far tendere a 0 la distanza tra i gate dei 3 nMOS, si ha infatti in tal caso un unico gate largo 3L.
8) Influenza della pendenza della forma d´onda d´ingresso sul ritardo di una porta logica :
La pendenza della forma d´onda d´ingresso può modificare il ritardo di una porta, in particolare se i fronti sono molto ripidi allora il ritardo è determinato prevalentemente dai percorsi di carica e scarica mentre se l´ingresso varia lentamente allora contribuisce al ritardo della uscita, in particolare si ha  dove tdr-step è il tempo di ritardo in salita che si ha per un ingresso a gradino , tinput-fall è il tempo di discesa della ingresso e
dove tdr-step è il tempo di ritardo in salita che si ha per un ingresso a gradino , tinput-fall è il tempo di discesa della ingresso e ![]() .
.
In maniera analoga si ha  con
con ![]() .
.
9) Modelli switch per calcolare il ritardo di una porta :
Sono modelli per il calcolo di ritardi di porte complesse, si basano sul considerare i MOS come resistenze che caricano e scaricano delle capacità, nella fattispecie si sono affermati i seguenti 3 modelli :
a) RC
 dove Rpull-down è la resistenza totale incontrata nel percorso di pull-down mentre Cpull-down sono tutte le capacità relative ai nodi coinvolti nelle commutazioni. In maniera analoga si calcola tdr .
dove Rpull-down è la resistenza totale incontrata nel percorso di pull-down mentre Cpull-down sono tutte le capacità relative ai nodi coinvolti nelle commutazioni. In maniera analoga si calcola tdr .
b) Penfield-Rubenstein
 dove Ri è la resistenza dal nodo i verso VSS se si considera il fall-time (…o verso VDD se si considera il rise-time) mentre Ci è la capacità al nodo i .
dove Ri è la resistenza dal nodo i verso VSS se si considera il fall-time (…o verso VDD se si considera il rise-time) mentre Ci è la capacità al nodo i .
c) Slope
Definisce il tempo di salita intrinseco come il tempo di salita che si avrebbe se in ingresso venisse applicato un gradino. Il tempo di salita effettivo viene suddiviso per il tempo di salita intrinseco.
d) Penfield-Rubenstein Slope Delay
È una combinazione dello Slope e del Penfield-Rubenstein.
10) Modello per calcolare il ritardo di circuiti molto complessi :
Il ritardo di una data porta viene determinato mediante un simulatore dal quale si ottiene un´equazione del tipo ![]() dove tinternal è un ritardo fisso introdotto dalla porta mentre toutput è un ritardo proporzionale al carico k .
dove tinternal è un ritardo fisso introdotto dalla porta mentre toutput è un ritardo proporzionale al carico k .
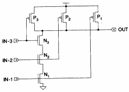
11) Body – effect nei ritardi delle porte logiche :
Gli nMOS più vicini all´uscita di una porta nand hanno necessariamente una Vsb ¹ 0 , il che fa si che essi siano più lenti nelle commutazioni effetto che diviene evidente se la capacità d´uscita è comparabile alle capacità interne.
Consideriamo le due seguenti porte nand :
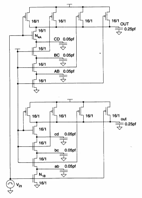
la nand in alto ha tutti gli nMOS accesi tranne quello in alto, ne deriva che il suo source è a massa e quindi quando l´ingresso passa ad 1 l´uscita commuta rapidamente a 0 . Nella nand in basso invece tutti gli nMOS in alto sono attivi mentre quello in basso è inizialmente interdetto, ne segue che le capacità saranno tutte cariche al livello alto e quando l´ingresso passa alto, si dovranno scaricare prima tutte per consentire la commutazione della uscita dal livello alto al livello basso che pertanto avviene in un tempo più lungo di quanto non si abbia per la nand in alto.
Per minimizzare gli effetti del body – effect si possono utilizzare le seguenti strategie :
a) minimizzare le capacità dei nodi interni
b) porre i MOS aventi i segnali che arrivano per ultimi il più vicino possibile all´uscita
12) Dimensionamento dei transistor nelle porte CMOS :
In genere si fa Wp = 2 Wn in modo da equalizzare i tempi di carica e di scarica, ma in tal modo si ha un aumento della area occupata e della dissipazione dinamica pertanto quando possibile si applicano le seguenti strategie :
a) una coppia di inverter posti in serie con Wp = 2 Wn da luogo allo stesso ritardo generato da una coppia di inverter aventi Wp = Wn , per dimostrarlo siano R e Ceq rispettivamente la resistenza e la capacità equivalente di un MOS avente dimensioni unitarie, e consideriamo i ritardi per le seguenti configurazioni :
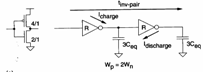 La capacità è 3Ceq in quanto è il parallelo della capacità della nMOS che vale Ceq e della capacità del pMOS che è 2Ceq in quanto Wp = 2Wn , ne deriva che il tempo di discesa è
La capacità è 3Ceq in quanto è il parallelo della capacità della nMOS che vale Ceq e della capacità del pMOS che è 2Ceq in quanto Wp = 2Wn , ne deriva che il tempo di discesa è ![]() mentre il tempo di salita è
mentre il tempo di salita è ![]() in quanto il pMOS avendo Wp = 2Wn ha resistenza dimezzata rispetto all´nMOS minimum-size , pertanto globalmente il ritardo è
in quanto il pMOS avendo Wp = 2Wn ha resistenza dimezzata rispetto all´nMOS minimum-size , pertanto globalmente il ritardo è ![]() .
.

Essendo Wp = 2Wn la capacità della nMOS è uguale a quella del pMOS pertanto si avrà 2Ceq , ne deriva che il tempo di discesa è ![]() mentre il tempo di salita è
mentre il tempo di salita è ![]() in quanto il pMOS avendo Wp = Wn ha resistenza dimezzata rispetto all´nMOS minimum-size , pertanto globalmente il ritardo è
in quanto il pMOS avendo Wp = Wn ha resistenza dimezzata rispetto all´nMOS minimum-size , pertanto globalmente il ritardo è ![]() ossia lo stesso riscontrato per la altra configurazione, con la differenza che in quest´ultima viene minimizzata la area in quanto si ha Wp = Wn , naturalmente questo cambio di W influenza il b e conseguentemente anche Vinv la quale però può variare al massimo del 15%.
ossia lo stesso riscontrato per la altra configurazione, con la differenza che in quest´ultima viene minimizzata la area in quanto si ha Wp = Wn , naturalmente questo cambio di W influenza il b e conseguentemente anche Vinv la quale però può variare al massimo del 15%.
b) Per pilotare carichi molto elevati si possono inserire degli inverter in cascata di dimensioni via via crescenti in modo però da minimizzare il ritardo, la area e la dissipazione.
![]()
Sia a la aumento percentuale delle dimensioni di un inverter rispetto al precedente e td il ritardo medio introdotto da un inverter a dimensioni minime, allora il ritardo introdotto da ogni stadio è atd mentre il ritardo totale è natd che se poniamo  diviene
diviene  dove la quantità frazionaria è l´unica sulla quale si può intervenire, si ha che essa è minima per a = e @ 2.7 tuttavia in genere nelle applicazioni si può avere a compreso tra 2 e 10.
dove la quantità frazionaria è l´unica sulla quale si può intervenire, si ha che essa è minima per a = e @ 2.7 tuttavia in genere nelle applicazioni si può avere a compreso tra 2 e 10.
13) Potenza dissipata da un circuito CMOS :
![]()
a)  Ps è dovuto alla dissipazione statica che nel caso del CMOS è esclusivamente dovuta ai diodi parassiti polarizzati inversamente per ognuno dei quali si ha
Ps è dovuto alla dissipazione statica che nel caso del CMOS è esclusivamente dovuta ai diodi parassiti polarizzati inversamente per ognuno dei quali si ha 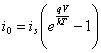 e quindi considerando n dispositivi, la potenza statica dissipata è
e quindi considerando n dispositivi, la potenza statica dissipata è  , per un tipico inverter alimentato a 5V si ha Ps @ 1nW .
, per un tipico inverter alimentato a 5V si ha Ps @ 1nW .
b) Pd è la potenza dinamica dissipata per caricare e scaricare la capacità di carico, considerando in ingresso un´onda quadra ideale avente periodo tp si ha  .
.
c) Psc è la potenza dissipata in corto circuito quando l´ingresso non è un´onda quadra ideale ma più realmente si presenta come una ripetizione di trapezi come evidenziato in figura , si ha ![]() con
con  , si ottiene
, si ottiene ![]() dove trf è il tempo di salita o discesa della forma d´onda d´ingresso e può dar luogo a variazioni del 20% nel caso di inverter caricati. .
dove trf è il tempo di salita o discesa della forma d´onda d´ingresso e può dar luogo a variazioni del 20% nel caso di inverter caricati. .
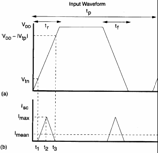
Il calcolo della potenza dissipata deve essere effettuato per ogni capacità alla frequenza per la quale è operativa.
14) Charge - sharing :
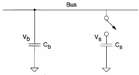 Quando si voglia campionare un bus caratterizzato da una capacità Cb con un dispositivo caratterizzato da una capacità Cs si deve fare in modo che la tensione VR letta sia pressochè uguale alla tensione Vb presente sul bus, in particolare prima della chiusura della interruttore si ha Qb=CbVb ed anche Qs=CsVs mentre dopo la chiusura si ha
Quando si voglia campionare un bus caratterizzato da una capacità Cb con un dispositivo caratterizzato da una capacità Cs si deve fare in modo che la tensione VR letta sia pressochè uguale alla tensione Vb presente sul bus, in particolare prima della chiusura della interruttore si ha Qb=CbVb ed anche Qs=CsVs mentre dopo la chiusura si ha ![]() che nel caso Vb=VDD>>Vs si riduce a
che nel caso Vb=VDD>>Vs si riduce a  che quindi rispetta la condizione solo se Cb>>Cs , nelle applicazioni si ha Cb>10Cs . Consideriamo ora una porta nand statica a 2 ingressi inizialmente entrambe a 0 e quindi l´uscita è ad 1, quando l´nMOS in alto passa ad 1 l´uscita deve ancora essere 1 tuttavia per charge sharing si abbassa rispetto a VDD in quanto c´è la capacità parassita posta tra i due MOS .
che quindi rispetta la condizione solo se Cb>>Cs , nelle applicazioni si ha Cb>10Cs . Consideriamo ora una porta nand statica a 2 ingressi inizialmente entrambe a 0 e quindi l´uscita è ad 1, quando l´nMOS in alto passa ad 1 l´uscita deve ancora essere 1 tuttavia per charge sharing si abbassa rispetto a VDD in quanto c´è la capacità parassita posta tra i due MOS .
15) Resa di un wafer :
Si tratta del rapporto tra il n° di chip buoni presenti su di un wafer ed il n° totale di chip presenti sullo stesso, essa è funzione della area A del chip e della densità di difetti D, si hanno i seguenti modelli :
a) Seed ![]() è un modello utilizzato per chip molto grandi aventi una resa inferiore al 30%
è un modello utilizzato per chip molto grandi aventi una resa inferiore al 30%
b) Murphy 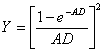 è un modello utilizzato per chip piccoli con rese superiori al 30%.
è un modello utilizzato per chip piccoli con rese superiori al 30%.
La resa può essere aumentata aumentando la ridondanza dei circuiti.
