Meccanica ondulatoria

1) Relazione di De Broglie :

De Broglie sostiene che la luce abbia una doppia natura, particellare ed ondulatoria per cui ad un elettrone è associata sia una massa che un´onda. La relazione che lega la lunghezza d´onda l della radiazione alla sua quantità di moto .

 

2) Osservabili ed operatori :

Gli osservabili sono proprietà meccaniche che possono essere misurate come la posizione x, la quantità di moto p e l´energia E mentre gli operatori sono utilizzati in meccanica quantistica ed in meccanica ondulatoria ed in sostanza si tratta di particolari istruzioni matematiche. Osservabili ed operatori sono riuniti da una importante relazione che afferma

che i soli valori possibili misurabili per un osservabile sono quelli per cui .

Sono di particolare importanza l´operatore quantità di moto  e l´operatore energia totale   che è anche denominato Hamiltoniana.

 

3) Valore medio di una sequenza di molte misure di un osservabile :

 

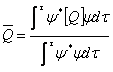
4) Equazione di Schroedinger :

Essa descrive la funzione d´onda y(x,y,z,t) ossia l´onda associata ad una particella dotata di massa. 

 .

 

5) Significato fisico della funzione d´onda :

Il modulo quadro della funzione d´onda y cioè rappresenta la densità di presenza della particella nel punto x,y,z al tempo t . Tale densità va moltiplicata per una costante di normalizzazione che renda unitario l´integrale calcolato su tutto lo spazio.

 

6) Principio di indeterminazione di Heisenberg :

Afferma che vi sono coppie di variabili coniugate per le quali quando aumenta il grado di conoscenza di una diminuisce automaticamente il grado di conoscenza della altro, la coppia di variabili di interesse in quantistica è la quantità di moto e la posizione della elettrone ebbene Heisenberg afferma che date le ridotte dimensioni di questa particella, quando noi mediante un protone cerchiamo di individuarne la posizione sappiamo di averlo preso ma il fotone cede all´elettrone energia e lo manda a sbattere chissà dove. Il principio di indeterminazione di Heisenberg afferma che il prodotto delle incertezze vale  .

 

7) Soluzione della equazione di Schroedinger nel caso di particella libera :

Occorre porre V = 0 nella equazione di Schroedinger indipendente dal tempo e limitarsi al caso unidimensionale, si ottiene :                                  

In sostanza si ha che la particella può essere ovunque, abbiamo cioè una totale indeterminazione sulla posizione essendo istante per istante completamente nota la quantità di moto.

 

8)       Condizione di Bragg :

È la condizione da imporre alla lunghezza d´onda di una radiazione incidente con un angolo q rispetto alla asse x affinché possa dar luogo ad interferenza costruttiva se inviata contro dei piani reticolari separati dalla distanza d.  La condizione 

si ottiene individuando il piano reticolare immediatamente sottostante, disegnando il raggio che riflette su di esso e valutando la lunghezza ottica in più rispetto alla riflessione sul piano sovrastante. Affinché i due raggi siano in fase occorre che tale differenza di percorso sia un multiplo n della lunghezza d´onda l. Occorre utilizzare una lunghezza d´onda prossima alla distanza tra i piani pertanto è necessario utilizzare come sonda dei raggi x.

 

9) Calcolo di Laue per la ampiezza della onda diffusa e reticolo reciproco :

Si tratta di un calcolo che viene introdotto per limitare l´errore di base del calcolo di Bragg, ossia il considerare i piani reticolari come degli specchi e quindi perfettamente riflettenti.

Si consideri uno dei punti del reticolo come origine O , un punto situato a distanza r da esso viene investito da un´onda piana  che considereremo sempre al tempo t = 0 . In r si ha   ma questo punto diviene sorgente di onde sferiche secondarie per cui la ampiezza della radiazione sul rivelatore posto a distanza r da r e R dall´origine è   dove kr sono i moduli perché in un´onda sferica i due vettori sono sempre paralleli.

Il modulo quadro della ampiezza della radiazione rilevata è   il massimo della quale si ottiene annullando il denominatore ossia per  e quindi   dove q è un intero.

Si ottengono quindi le condizioni di Laue per la massima diffrazione :

                                                            

dove q, r, s   sono dei numeri interi esse sono alla base della definizione del reticolo reciproco in quanto i vettori di traslazione dello stesso                           

sono tali che una qualsiasi loro combinazione lineare soddisfi le equazioni di Laue per la massima diffrazione.