Segnali certi nel dominio del tempo

1) Spazio funzionale :

E´ costituito dall´insieme dei segnali per cui esiste ed è finita la norma p_esima .

Per p = 1  si parla di segnali assolutamente integrabili mentre per p = 2  si parla di segnali quadraticamente integrabili.

 

2) Potenza istantanea del segnale :

È il modulo quadro del segnale stesso cioè |x(t)|² .

 

3) Energia del segnale :

L´energia è l´integrale della potenza istantanea  .

 

4) Segnali di energia :

Sono segnali per i quali E_xx  assume un valore finito, il loro spazio funzionale è L₂ essi possono essere sia limitati che illimitati nel tempo, in questo caso si individua una durata pratica T all´esterno della quale si assume che il segnale valga zero. Tutti i segnali pratici sono segnali di energia in quanto hanno durata limitata.

 

5) Potenza media del segnale :

Nel caso un segnale s(t) sia illimitato nel tempo e non abbia energia finita, si considera la potenza media temporale del segnale         essendo       il segnale troncato.

 

6) Segnale di potenza :

È un segnale per il quale assume un valore finito la potenza media.

 

7) Valor medio di un segnale :

   , esso è diverso da 0 solo per i segnali di potenza.

 

8) Componente alternata del segnale x(t) :

 

9) Fattore di picco :

È riferito ai segnali simmetrici, i quali sono privi di componente continua ed hanno valore massimo e valore minimo opposti , si ha :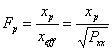                                                  

 

10) Funzione di replica :

soltanto se il periodo T₀ è maggiore del periodo T_y del segnale sorgente si ottiene un andamento simile ad esso.

 

11) Potenza di un segnale periodico ottenuto per ripetizione di un segnale di durata finita :

essendo E_xx0 l´energia calcolata all´interno di un periodo, essa coincide con E_YY solo se T_Y < T₀ .

 

12) Energia per sequenze :

si calcola quindi l´energia del segnale continuo ottenuto da quello discreto mediante l´operazione di “tenuta” , inoltre per convenzione si assume T = 1.

 

13) Potenza per sequenze :

si calcola quindi la potenza del segnale continuo ottenuto da quello discreto mediante l´operazione di “tenuta” , inoltre per convenzione si assume T = 1.

 

14) Funzione di intercorrelazione temporale o correlazione mutua temporale :

Individua il grado di somiglianza tra 2 funzioni    .

Si deve porre attenzione al fatto che non coincide con il prodotto di convoluzione.

 

15) Energie mutue :

Si tratta della funzione di intercorrelazione calcolata in t = 0   .

 

16) Funzione di indice di intercorrelazione temporale :

È il rapporto tra la funzione di intercorrelazione e la radice del prodotto delle energie   risulta inoltre |r_xy(t)| £ 1 .

 

17) Funzione di autocorrelazione di segnali di energia :

si tratta cioè di una funzione hermitiana con valore reale nell´origine C_xx(0) = E_xx , misura la affinità tra un segnale traslato nel tempo rispetto a quello che non trasla.

 

18) Prodotto scalare di 2 segnali :

Si tratta del valore nell´origine della funzione di intercorrelazione tra due segnali    , misura la affinità dei due segnali non traslati.

 

19) Segnali paralleli, antipodali, ortogonali :

Si valuta l´indice di intercorrelazione  si ha :

a) r_xy  = 1              Þ           segnali paralleli

b) r_xy  = 0              Þ           segnali ortogonali

c) r_xy  = -1             Þ           segnali antipodali

 

20) Funzione di intercorrelazione di segnali di potenza :

 

21) Potenze mutue :

Si tratta dei valori assunti nell´origine dalle funzioni di intercorrelazione  P_xy = R_xy(0) = R^*_yx(0) = P^*_yx .

 

22) Funzione di indice di intercorrelazione temporale di segnali di potenza :

È una funzione adimensionale definita  , il suo modulo è sempre minore di 1 .

 

23) Funzione di covarianza temporale per segnali di potenza :

È la funzione di intercorrelazione temporale delle componenti a valor medio nullo :

 

24) Funzione di autocorrelazione temporale di segnali di potenza :

Individua la affinità di un segnale traslato nel tempo con quello non traslato                           è dunque una funzione hermitiana.

 

25) Funzione di autocovarianza temporale :

 

26) Famiglia di segnali incorrelati :

Una famiglia di segnali si dice incorrelata se tutte le funzioni di covarianza sono nulle K_xy(t)=0 .

 

27) Famiglia di segnali incoerenti :

È di un insieme di segnali di potenza per i quali per ogni t sono nulle tutte le funzioni di intercorrelazione C_xy(t) = 0 .

 

28) Sequenze di intercorrelazione tra sequenze ad energia finita :

 

29) Sequenze di autocorrelazione temporali per sequenze a energia finita :

essa da una misura della velocità di variazione del segnale stesso.

 

30) Sequenze di autocorrelazione temporali per sequenze a potenza finita :

 

31) Sequenze di autocovarianza :