Sistemi di asservimento
1) Sistema di asservimento :
Si tratta di un sistema nel quale l´ingresso è variabile nel tempo con una dinamica comparabile con quella del processo stesso e quindi sono importanti oltre alle specifiche a regime anche le specifiche sul transitorio.
2) Specifica basilare di un qualsiasi sistema :
Qualsiasi sistema deve sempre essere caratterizzato dalla stabilità.
3) Specifiche di progettazione relative al comportamento a regime :
a) tipo di sistema ossia numero di poli nell´origine.
b) errore a regime in corrispondenza ad un dato ingresso canonico di riferimento.
4) Specifiche nel dominio del tempo :
Sono riferite alla risposta indiciale, di consueto a ciclo chiuso, esse sono :
Tempo all´eminvalore :
intervallo di tempo che la risposta indiciale impiega per giungere a metà del valore di regime.
Tempo di risposta :
intervallo di tempo che intercorre tra lo 0,1 e lo 0,9 del valore di regime della risposta indiciale.
Sovraelongazione :
valore massimo raggiunto dalla risposta indiciale qualora sovraelongante.
Pseudoperiodo :
È il periodo delle oscillazioni smorzate presenti nella risposta indiciale, si calcola a partire dalla 2ª intersezione della risposta indiciale con il valore di regime.
Tempo di assestamento :
È il tempo in corrispondenza del quale la risposta indiciale raggiunge lo 0,05 del valore di regime.
5) Specifiche nel dominio della frequenza :
Con riferimento alla risposta armonica a ciclo chiuso, si ha :
Modulo alla risonanza :
valore massimo assunto dal modulo della risposta armonica.
Pulsazione di banda passante :
pulsazione per la quale il modulo della risposta armonica si riduce di 3dB rispetto al valore che assume per w®0.
con riferimento alla risposta armonica a ciclo aperto si considerano invece il margine di guadagno mg , il margine di fase mj e la pulsazione di attraversamento wt .
Sintesi per tentativi nel dominio di jw
6) Tipologie di sistemi per i quali si utilizza la sintesi per tentativi in jw :
Viene utilizzata per sistemi a fase minima ossia aventi tutti i poli e gli zeri nel semipiano sinistro
7) Legami globali :
Si tratta di formule empiriche che legano le specifiche nel tempo con le specifiche in frequenza, le più importanti sono:
![]() a patto che la sovraelongazione S sia minore di 0,1
a patto che la sovraelongazione S sia minore di 0,1
![]() a patto che il modulo alla risonanza Mr sia compreso tra 2dB e 4dB.
a patto che il modulo alla risonanza Mr sia compreso tra 2dB e 4dB.
8) Considerazioni sulle specifiche nella sintesi in jw :
Le specifiche che sono date nel dominio del tempo tr ed S debbono essere tramutate in specifiche nel dominio della frequenza wB ed Mr tramite le relazioni ![]() e
e ![]() inoltre è più agevole progettare il compensatore a ciclo aperto pertanto occorre passare dalle specifiche a ciclo chiuso wB ed Mr alle specifiche a ciclo aperto mj ed wt .
inoltre è più agevole progettare il compensatore a ciclo aperto pertanto occorre passare dalle specifiche a ciclo chiuso wB ed Mr alle specifiche a ciclo aperto mj ed wt .
9) Utilizzo della carta di Nichols nel passaggio dalle specifiche a ciclo chiuso alle specifiche a ciclo aperto :
Viene utilizzata la carta di Nichols in quanto la stessa curva relativa alla risposta armonica, se letta in coordinate cartesiane esprime la stessa a ciclo aperto mentre se letta in coordinate curvilinee lungo le curve a modulo costante, esprime la risposta armonica a ciclo chiuso. Si ricordi che l'intersezione della F(jw) con l'asse a 0dB individua il margine di fase e la pulsazione corrispondente è detta pulsazione di attraversamento wt .
10) Passaggio dalla specifica sul modulo alla risonanza al margine alla specifica sul margine di fase :
Mr sulla carta di Nichols è pari al valore della curva a modulo costante più elevato che risulti tangente alla G(jw), l'intersezione di tale curva a modulo costante con l'asse a 0dB individua un margine di fase che è senz'altro minore del margine di fase della G(jw) pertanto, assumendolo come specifica, si ha anche un margine di sicurezza. In realtà il modulo alla risonanza Mr è compreso tra 1dB e 5dB a cui corrispondono margini di fase mj compresi tra 54° e 33° .
11) Passaggio dalla specifica sulla banda passante wb alla specifica sulla pulsazione di attraversamento wt :
la pulsazione di attraversamento wt sulla carta di Nichols è individuata dalla intersezione tra la G(jw) e la retta a 0dB, la banda passante wb invece è individuata dalla intersezione tra la G(jw) e la curva a modulo costante a -3dB , questa interseca l'asse a 0dB per j=-90° . Considerando che le pulsazioni crescono dall'alto verso il basso lungo la curva che rappresenta la G(jw) ed osservando che il margine di fase per un sistema stabile è 30° < mj < 60° << 90° , si ha che la specifica su wb è rispettata se wt < wB , ulteriori considerazioni portano ad affermare che deve essere :
![]()
12) Reti standard :
Ci sono tre tipologie standard tutte aventi guadagno unitario e di cui la terza è costruita accoppiando le prime due:
a) rete ritardatrice o attenuatrice
b) rete anticipatrice
c) rete a sella
13) Rete ritardatrice :
Si ottiene posizionando un polo nel semipiano sinistro ed uno zero alla sua sinistra, viene utilizzata laddove si voglia ridurre la pulsazione di attraversamento qualora non ci siano problemi riguardo alla fase, dai diagrammi di Bode si evince infatti che tale rete consente sia di attenuare che di inserire un ritardo. In realtà la rete ritardatrice non è molto utilizzata proprio perché attenuando diminuisce la pulsazione di attraversamento wt , con essa diminuisce la banda passante wB e quindi il tempo di risposta tr del sistemainfatti si ha ![]() e
e ![]() . L'espressione generale di tale rete è
. L'espressione generale di tale rete è 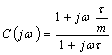 con m che varia tra 2 e 16 e consente di spostare la posizione dello zero rispetto al polo.
con m che varia tra 2 e 16 e consente di spostare la posizione dello zero rispetto al polo.
14) Rete anticipatrice :
Si ottiene posizionando uno zero nel semipiano sinistro ed un polo alla sua sinistra, viene utilizzata laddove per una data wt si voglia aumentare il margine di fase, dai diagrammi di Bode si osserva che questa rete però oltre ad anticipare aumenta anche il guadagno e quindi wt, essendo il diagramma delle fasi monotono decrescente tale effetto viene compensato accrescendo di un 10% la fase richiesta.L'espressione generale è 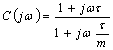 con m che varia tra 2 e 16 e consente di spostare la posizione del polo rispetto allo zero.
con m che varia tra 2 e 16 e consente di spostare la posizione del polo rispetto allo zero.
15) Sintesi per tentativi nel dominio di jw :
Occorre iterare la seguente procedura trattandosi di una sintesi per tentativi :
a) si soddisfa la specifica sull´errore a regime ottenendo il sistema precompensato
b) si soddisfa la specifica sulla banda passante facendo si che la pulsazione corrispondente w* sia maggiore della wt del sistema precompensato, a tal fine si può operare nei due seguenti modi :
1) si inserisce una rete ritardatrice che quindi riduce la wt ma diminuisce anche la fase, se ciò inficia la specifica sul margine di fase mj è necessario introdurre una rete anticipatrice quindi globalmente si necessità di una complessa rete a sella
2) qualora sia possibile è conveniente inserire un polo nell'origine in modo da svincolare la specifica sull'errore a regime dal guadagno e poi ridurre quest'ultimo e con esso la wt .
c) Si soddisfa la specifica sul modulo alla risonanza che va tradotta in una specifica sul margine di fase tramite la apposita tabella e, qualora necessaria, si inserisce pertanto una rete anticipatrice la quale però incrementa anche il modulo per cui si deve far attenzione che non divenga wt > w* . Per progettare la rete anticipatrice si può operare in uno dei due seguenti modi :
1) in corrispondenza di wt si vede quanto deve essere la variazione della fase per soddisfare la specifica sul margine di fase mj ed al valore trovato si deve aggiungere un 10% intrinseco nell'uso della rete anticipatrice
2) si si posiziona sulla pulsazione desiderata w* e si valuta sia l'incremento di fase per soddisfare la specifica sul margine di fase, che l'eventale incremento del modulo necessario per spostare wt in w* .
Sintesi per tentativi nel dominio della variabile s
16) Quando si utilizza la sintesi per tentativi in s :
Nel caso di sistemi semplici a fase non minima oppure quando vengano fornite delle specifiche nel dominio del tempo quali lo smorzamento x , la pulsazione naturale wn e la massima costante di tempo t ammissibile per il sistema.
17) Effetto della limitazione dello smorzamento x sul luogo delle radici :
Si ha che il luogo deve essere compreso nel semipiano sinistro tra 2 rette passanti per l´origine e formanti con la asse immaginario un angolo il cui arcoseno sia pari allo smorzamento x .
18) Effetto della limitazione della pulsazione naturale wn sul luogo delle radici :
Il luogo delle radici deve essere compreso nel semipiano sinistro all´interno di 2 rette orizzontali la cui ordinata corrisponde alla pulsazione di risonanza che per un dato smorzamento x è legata alla pulsazione naturale wn dalla relazione ![]() .
.
19) Effetto della limitazione della massima costante di tempo sul luogo delle radici :
Il luogo delle radici deve essere compreso a sinistra di una retta verticale passante per il più piccolo polo corrispondente al massimo tempo di salita che il sistema può presentare.
20) Considerazioni sugli zeri a parte reale positiva :
Non sono una realtà fisica, essi si generano quando per tenere conto dei ritardi si approssima l'esponenziale con gli sviluppi in serie di Mac Laurin.
21) Come stabilizzare i sistemi a fase non minima :
Occorre aggiungere un numero di zeri nel semipiano sinistro tale che l´eccesso poli-zeri sia pari ad uno ma al contempo, affinchè il compensatore sia fisicamente realizzabile, si deve aggiungere un numero di poli non minore del numero di zeri, per soddisfare entrambe le specifiche i poli che si debbono necessariamente introdurre vengono posti all´infinito dove non hanno influenza mentre gli zeri vengono posti molto vicino all'origine in modo da attrarre il baricentro. In sostanza si deve far si che per un dato intervallo di guadagni tutti i rami del luogo siano contenuti all'interno della regione delimitata dalle specifiche su x , wn e t .
Sintesi diretta
22) Filosofia della sintesi diretta :
Ci si propone di avere una funzione di trasferimento a ciclo chiuso W(s) di tipo standard indipendentemente dal processo, a tal fine il compensatore è progettato in modo da effettuare delle cancellazioni nella funzione di trasferimento a ciclo aperto P(s) del processo da compensare, ciò determina che questa sintesi è applicabile unicamente a sistemi a fase minima in quanto le cancellazioni nel semipiano sinistro sono possibili solo per i sistemi ideali.
23) Tipologie di sintesi diretta :
Nella sintesi ad un grado di libertà si ha soltanto l'ingresso U(s) mentre nella sintesi a due gradi di libertà si ha sia l'ingresso U(s) che il disturbo D(s).
24) Relazione che descrive il compensatore :
Deve essere nota la funzione di trasferimento a ciclo chiuso desiderata ![]() , invertendo quest'ultima si ottiene l'espressione del compensatore
, invertendo quest'ultima si ottiene l'espressione del compensatore![]() .
.
25)Funzione di trasferimento a ciclo chiuso e valore dei coefficienti :
![]()
dove la produttoria a denominatore indica dei poli lontani che vengono inseriti per garantire la realizzabilità fisica del compensatore mentre i coefficienti del trinomio vengono scelti sulla base della risposta al transitorio richiesta, quindi :
a1 = 2xwn
a0 = wn2
mentre i termini a numeratore vengono scelti sulla base del valore della errore a regime, in particolare :
a) nel caso che si richieda un errore a regime nullo per ingressi di tipo gradino :
b0 = a0
b1 = qualsiasi
b) nel caso che si richieda un errore a regime nullo per ingressi di tipo rampa :
b0 = a0
b1 = a1
il valore di tali coefficienti è determinato da considerazioni sulla funzione di trasferimento di errore nel caso di retroazione unitaria ![]() .
.
Sintesi per assegnazione dei poli
26) Filosofia della sintesi per assegnazione dei poli :
È applicabile ad ogni sistema, sia a fase minima che non, si basa sull'imporre la posizione degli zeri della funzione di trasferimento a ciclo chiuso e conseguentemente si determinano i coefficienti del compensatore il cui denominatore deve possedere grado l ³ n-1 essendo n il grado del denominatore del processo da compensare, mentre il numeratore del compensatore possiede lo stesso grado del denominatore dello stesso.
Sintesi per assegnazione degli autovalori
27) Sintesi per reazione dallo stato :
Si ha un sistema lineare e stazionario controllabile del quale sono note tutte le variabili di stato ossia il vettore di stato, si vuole determinare un vettore di guadagni Kc il quale consenta di far si che gli autovalori della matrice dinamica corrispondente al sistema ![]() siano tutti in una determinata regione del piano complesso in accordo con il risultato che si desidera ottenere dal sistema, ad esempio se si richiede la stabilità asintotica questi autovalori debbono trovarsi tutti nel semipiano sinistro. Se la matrice A è in forma di controllore si ottiene che l´ultima riga di Ac ha i coefficienti uguali a meno del segno ai coefficienti del polinomio caratteristico e quindi si ottiene un sistema di equazioni del 1° ordine da cui ricavare Kc che restituisce il polinomio caratteristico desisderato.
siano tutti in una determinata regione del piano complesso in accordo con il risultato che si desidera ottenere dal sistema, ad esempio se si richiede la stabilità asintotica questi autovalori debbono trovarsi tutti nel semipiano sinistro. Se la matrice A è in forma di controllore si ottiene che l´ultima riga di Ac ha i coefficienti uguali a meno del segno ai coefficienti del polinomio caratteristico e quindi si ottiene un sistema di equazioni del 1° ordine da cui ricavare Kc che restituisce il polinomio caratteristico desisderato.
Il problema di questa sintesi è che occorre conoscere tutto il vettore di stato il che può essere complesso e dispendioso.
28) Formula di Ackermann per la retroazione dallo stato :
Consente di individuare il vettore Kc quando la matrice Ac non sia posta in forma compagna, evitando in tal modo il tortuoso passaggio alla stessa, si ha :
![]()
essendo ![]() l'immagine di A attraverso il polinomio caratteristico Pc(A).
l'immagine di A attraverso il polinomio caratteristico Pc(A).
29) Stima dello stato :
Nella sintesi per reazione dallo stato era necessario conoscere tutto il vettore di stato mentre la stima di stato è una tipologia di sintesi che si ricava il valore dello stato del sistema a patto che esso sia osservabile e siano note le grandezze d´ingresso e d´uscita dello stesso.
30) Stato stimato :
Si tratta del vettore che si ottiene in uscita dal sistema avente come ingressi le grandezze d´ingresso e d´uscita del sistema assegnato, e che soddisfa la relazione ![]() .
.
31) Osservatore dello stato :
S´intende il sistema dinamico che effettua la stima dello stato, è anche detto stimatore ed è descritto dall'equazione di stato ![]() , scopo della stima dello stato è individuare le matrici F , h , g in modo che lo stato soddisfi la
, scopo della stima dello stato è individuare le matrici F , h , g in modo che lo stato soddisfi la ![]() a tal fine si trasformano secondo Laplace sia l'equazione del sistema che l'equazione dell'osservatore e si eguagliano le funzioni di trasferimento , si ottiene
a tal fine si trasformano secondo Laplace sia l'equazione del sistema che l'equazione dell'osservatore e si eguagliano le funzioni di trasferimento , si ottiene ![]() .
.
Raccogliendo al 1° membro i coefficienti di ![]() ed estraendo il termine
ed estraendo il termine ![]() quest'ultimo si può semplificare e si ottiene
quest'ultimo si può semplificare e si ottiene ![]() da cui si deduce che per lo stimatore si ha
da cui si deduce che per lo stimatore si ha ![]() e
e ![]() .
.
Per ricavare il vettore g si deve ricavare la dinamica dell'errore di stima, in particolare si ha ![]() pertanto si trova che l'errore della stima ha la stessa dinamica della stima il che implica che scegliamo g in modo da avere uno stimatore asintoticamente stabile, l'errore di stima tende a 0 indipendentemente dall'errore iniziale pertanto si deve scegliere g in modo che gli autovalori della matrice
pertanto si trova che l'errore della stima ha la stessa dinamica della stima il che implica che scegliamo g in modo da avere uno stimatore asintoticamente stabile, l'errore di stima tende a 0 indipendentemente dall'errore iniziale pertanto si deve scegliere g in modo che gli autovalori della matrice ![]() siano tutti a parte reale negativa. Se la matrice A0 è in forma di osservatore si ottiene che l'ultima colonna ha i coefficienti uguali a meno del segno ai coefficienti del polinomio caratteristico e quindi si ottiene un sistema di equazioni del 1° ordine da cui ricavare il vettore g che restituisce il polinomio caratteristico.
siano tutti a parte reale negativa. Se la matrice A0 è in forma di osservatore si ottiene che l'ultima colonna ha i coefficienti uguali a meno del segno ai coefficienti del polinomio caratteristico e quindi si ottiene un sistema di equazioni del 1° ordine da cui ricavare il vettore g che restituisce il polinomio caratteristico.
32) Considerazioni sulla scelta degli autovalori della matrice A0 :
Sono senz´altro a parte reale negativa, inoltre da essi dipende la dinamica dello stimatore la quale deve essere più rapida di almeno un ordine di grandezza rispetto alla dinamica del sistema e quindi questi autovalori debbono trovarsi molto più a sinistra rispetto agli autovalori del sistema.
33) Formula di Ackermann per la stima dello stato :
È una formula che consente di calcolare il vettore g quando la matrice A non sia in forma canonica di osservatore, si ha: 
dove ![]() è l'immagine di A attraverso il polinomio caratteristico Po(l).
è l'immagine di A attraverso il polinomio caratteristico Po(l).
34) Proprietà di separazione :
È una proprietà importante che si riferisce alla sintesi per retroazione dallo stato stimato, consente di progettare separatamente ed indipendentemente il vettore riga kc ed il vettore colonna g , si ha ![]() .
.
Si ottiene ponendo l'osservatore nello schema a controreazione, si scrivono quindi le equazioni del sistema
![]()
![]()
![]()
![]()
da cui sostituendo la ![]() nella 2ª e sostituendo questa nella prima e considerando come vettore di stato per il sistema retroazionato
nella 2ª e sostituendo questa nella prima e considerando come vettore di stato per il sistema retroazionato ![]() si ottengono le equazioni
si ottengono le equazioni ![]() cui corrisponde la matrice dinamica
cui corrisponde la matrice dinamica ![]() e ricordando che il polinomio caratteristico per una matrice triangolare si ottiene come prodotto dei termini sulla diagonale, il teorema è dimostrato.
e ricordando che il polinomio caratteristico per una matrice triangolare si ottiene come prodotto dei termini sulla diagonale, il teorema è dimostrato.
