Il luogo delle radici

1) Luogo delle radici :

È una tecnica che consente di rappresentare graficamente gli effetti del passaggio da ciclo aperto a ciclo chiuso, in sostanza si ha che al variare del guadagno k i poli si spostano determinando in tal modo la stabilità o l'instabilità del sistema, inoltre da poli reali a ciclo aperto si possono anche creare dei poli complessi coniugati a ciclo chiuso i quali se il sistema è stabile determinano una risposta oscillatoria smorzata dovuta a x ed w_i che nelle specifiche viene richiesta di lieve entità.

2) Sistema a stabilità regolare :

È un sistema che risulta stabile per un intervallo del guadagno k compreso tra 0 ed un valore limite superiore k_Lche può coincidere con ¥ , tale guadagno individua i poli posti sulla asse immaginario. Si parla di sistema a stabilità paradossale in quanto aumentando il guadagno si và verso la stabilità.

3) Sistema a stabilità condizionata :

È un sistema che è stabile se il guadagno è contenuto in un intervallo del guadagno k compreso tra due valori finiti.

4) Sistema a stabilità paradossale :

È un sistema che risulta stbile per un intervallo del guadagno compreso tra un valore limite finito k_L e ¥.

5) Luogo positivo :

È anche detto luogo delle radici e corrisponde alla posizione delle radici della equazione caratteristica della funzione di trasferimento del sistema a ciclo chiuso per un guadagno k > 0.

6) Luogo complementare :

È anche detto luogo negativo e corrisponde alla posizione delle radici della equazione caratteristica della funzione di trasferimento del sistema a ciclo chiuso per un guadagno k < 0. È importante per lo studio dei sistemi a retroazione positiva, e nel caso in cui un sistema sia stabile solo per valori negativi di k.

7) Relazione fondamentale per la costruzione del luogo delle radici :

Essendo si ha che l´equazione caratteristica è verificata se il che implica una condizione sui moduli ed una condizione sulle fasi.

8) Condizione dei moduli :

La relazione fondamentale è verificata per quanto riguarda i moduli se il modulo della trasferenza a ciclo aperto è , questa condizione non consente di tracciare il luogo in quanto per ogni k è soddisfatta da infiniti punti del piano, tuttavia una volta che il luogo è stato tracciato tramite la condizione sui moduli consente di graduarlo in k infatti per ogni punto s_i appartenente al luogo si può ricavare il k ad esso associato quale rapporto tra la produttoria delle lunghezze dei vettori che congiungono i poli della F(s) con s_i e la produttoria delle lunghezze dei vettori che congiungono gli zeri della F(s) con s_i ossia .

9) Condizione delle fasi :

La relazione fondamentale è verificata per quanto riguarda le fasi se la fase della trasferenza a ciclo aperto F(s) è essendo r un intero positivo o nullo. In sostanza un punto s_i del piano complesso appartiene al luogo positivo se la somma degli angoli rispetto al piano orizzontale dei vettori tracciati dagli zeri e dai poli della F(s) verso il punto s_i è multiplo dispari di ±180° . In pratica si utilizza r=0 e per k>0 si prende il meno.

10) Ramo del luogo completo delle radici :

È il luogo dei punti del piano complesso percorso da una delle radici della equazione caratteristica quando k varia tra -¥ e +¥ .

11) Numero di rami del luogo delle radici :

Il numero di rami è pari al più grande tra il numero dei poli n ed il numero degli zeri m della funzione di trasferimento a ciclo aperto F(s).

12) Punti del luogo delle radici corrispondenti a k = 0 :

Sono i poli della F(s) infatti , sostituendo k=0 si ottiene .

13) Punti del luogo delle radici corrispondenti a k = ±¥ :

Sono gli zeri della F(s) infatti dalla condizione sui moduli si ha infatti per k®¥ si ha 0 al 2° membro e quindi per verificare l'uguaglianza deve essere 0 anche NumF(s) il che accade se ci troviamo negli zeri della F(s).

14) Simmetrie del luogo completo delle radici :

Si ha sempre una simmetria rispetto alla asse reale infatti l´equazione caratteristica è a coefficienti reali pertanto le sue radici sono reali o a coppie complesse coniugate. Sono possibili anche simmetrie di poli e zeri rispetto ad altri assi i quali debbono necessariamente essere verticali in quanto si ottengono per trasformazioni geometriche dell'asse reale che debbono però sempre rispettare la simmetria rispetto ad una coppia di poli.

15) Numero di rami con cui diverge ad infinito il luogo positivo e relativo angolo :

Il luogo positivo diverge ad infinito con |n-m| rami , la angolo vale , con r intero positivo quindi se un sistema presenta un eccesso poli-zeri uguale a 0 non ha senso la schematizzazione dello 0 all´infinito. Si deduce dalla condizione sulle fasi osservando che quando il punto va all´infinito tutti i vettori che lo congiungono con poli e zeri sono paralleli quindi hanno la stessa fase. Si osservi che gli asintoti così individuati non fanno parte del luogo e quindi sia i rami del luogo positivo che quelli del luogo negativo possono intersecare gli asintoti stessi.

16) Baricentro del luogo e formule per individuarlo :

Si tratta del punto della asse reale che risulta essere intersezione degli 2|n-m| asintoti, nei sistemi a ciclo chiuso esso risulta essere invariante al variare di k , è individuato dalla formula 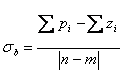la quale si può semplificare considerando le sole parti reali dato che poli e zeri sono complessi coniugati e quindi le parti immaginarie si elidono.

17) Condizioni di appartenenza del luogo positivo alla asse reale :

Appartengono al luogo positivo tutti i punti della asse reale che lasciano alla loro destra un numero complessivamente dispari di poli reali e di zeri reali della funzione di trasferimento a ciclo aperto, contati ognuno con la rispettiva molteplicità. Si dimostra a partire dalla condizione sulle fasi osservando che il vettore che congiunge un polo con un punto s corrisponde un contributo in fase di -180° se il polo si trova a destra oppure di 0° se il polo si trova a sinistra del punto s, mentre se a destra del punto s si trova uno zero, il contributo in fase è di 180°.

18) Angolo di partenza da un polo :

È la angolo con il quale il ramo del luogo positivo si allontana dal polo, esso è dato dalla seguente relazione :

19) Angolo di arrivo in uno zero :

È la angolo con il quale il ramo del luogo positivo arriva negli zeri della F(s) si allontana dal polo, esso è dato dalla seguente relazione :

20) Come individuare i punti d´intersezione del luogo delle radici con la asse immaginario :

Si deve applicare il criterio di Routh individuando così i k per i quali il sistema è al limite di stabilità e quindi i poli sono sulla asse immaginario, sostituendo questo valore di k nell´equazione caratteristica si ottengono i valori di w.

21) Punti singolari del luogo delle radici :

Sono punti che rappresentano radici multiple della equazione caratteristica, ossia punti che appartengono contemporaneamente a più rami del luogo. Al luogo completo delle radici appartengono al più n+m-1 punti singolari.

Si distinguono i punti singolari semplici nei quali si incontrano rami appartenenti allo stesso luogo ed i punti singolari multipli nei quali si incontrano rami appartenenti sia al luogo positivo che al luogo negativo, tali punti sono individuabili esclusivamente nei poli multipli o zeri multipli della funzione di trasferimento a ciclo aperto F(s).

22) Relazione per individuare i punti singolari :

Uguagliando a zero la derivata della equazione caratteristica si trovano i punti singolari i quali al fine di appartenere al luogo debbono anche soddisfare la . La tratta numeri complessi e pertanto è di difficile soluzione , in sua vece si può utilizzare la 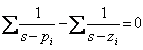la quale non individua i punti singolari multipli, ma questi si ottengono immediatamente in quanto coincidono con i poli multipli e gli zeri multipli della funzione di trasferimento a ciclo aperto F(s). Anche per questa equazione i punti trovati debbono poi soddisfare la .

23) Relazione tra la molteplicità ed i rami entranti nel punto singolare :

Se m è la molteplicità ossia il numero dei rami entranti nel punto allora questi dividono il piano in 2m settori di eguale ampiezza.

24) Numero di punti singolari tra un polo ed uno zero contigui :

C´è sempre un numero pari (0) di punti singolari tra un polo ed uno zero contigui.

25) Numero di punti singolari tra 2 poli o due zeri contigui :

C´è sempre un numero dispari (1) di punti singolari tra un polo ed uno zero contigui.

26) Verso delle frecce nel luogo positivo e nel luogo negativo :

In generale le frecce sono nel senso dei k crescenti da -¥ a +¥ quindi nel luogo negativo le frecce vanno dagli zeri (-¥) ai poli (0) , mentre nel luogo positivo vanno dai poli (0) agli zeri (+¥).

27) Analogia idraulica :

Per il luogo positivo si possono considerare i poli come sorgenti che pertanto respingono i rami del luogo e gli zeri come pozzi che pertanto attraggono i rami del luogo.

28) Condizioni sul sistema a ciclo aperto affinchè il sistema a ciclo chiuso sia sicuramente stabile :

I poli e gli zeri a ciclo aperto si trovano tutti nel semipiano sinistro, il baricentro è nel semiasse reale negativo ed il numero degli asintoti è minore o al più uguale a due.

Ritardi finiti

29) Quando occorre tener conto dei ritardi finiti nei sistemi reali :

Quando l´ordine di grandezza del ritardo risulta maggiore della più grande costante di tempo del sistema.

30) Equazione caratteristica in presenza di ritardi finiti :

Dalla si ha che i poli sono individuati dalla equazione caratteristica

31) Condizioni sui moduli e sulle fasi :

Dall'equazione caratteristica si ricava e quindi si ottengono la condizione sui moduli e la condizione sulle fasi .

32) Numero dei rami del luogo :

Il numero dei rami del luogo è infinito essendo infinito il numero di soluzioni della equazione caratteristica trascendente.

33) Tipologie dei punti del luogo completo delle radici per i quali si ha k=0 :

Dalla condizione sui moduli si vede che il 2° membro è infinito quindi l'uguaglianza è verificata se ci troviamo nei poli della F(s) o in s = -¥ .

34) Tipologie dei punti del luogo completo delle radici per i quali si ha k = ±¥ :

Dalla condizione sui moduli si vede che il 2° membro è zero quindi l'uguaglianza è verificata se ci troviamo negli zeri della F(s) o in s = +¥ .

35) Simmetrie del luogo completo delle radici :

Si ha simmetria rispetto all'asse reale in quanto sviluppando in serie di Taylor si ottiene un polinomio algebrico.

36) Applicazione del criterio di Routh nel caso di ritardi finiti :

Non si può applicare in quanto l'equazione caratteristica è trascendente quindi ha infinite soluzioni, le intersezioni con l'asse immaginario possono essere determinate in via approssimata con uno sviluppo in serie troncato dell'esponenziale.

37) Asintoti del luogo completo :

Gli asintoti sono infiniti e sono tutti paralleli alla asse delle ascisse e lo intersecano in corrispondenza ai punti .

38) Relazione tra i k degli infiniti luoghi alla intersezione con la asse immaginario :

Si ha che il k corrispondente al ramo che interseca la asse immaginario con la ordinata più piccola è inferiore ai k dei rami che intersecano la asse immaginario con ordinata maggiore.

39) Considerazioni riguardanti il tracciamento approssimato mediante sviluppo in serie :

Se si sviluppa in serie l'esponenziale, non si fa altro che aggiungere degli zeri il cui tipo (reale o complessi) e numero dipende dall'ordine dello sviluppo a cui ci si arresta, in particolare si vede che se ci si arresta ad un ordine dispari si ha uno zero reale il quale determina un luogo che non è compatibile con gli asintoti orizzontali inoltre il segno del termine di ordine dispari di potenza più elevata impone di scambiare il luogo positivo col negativo. Il numero degli zeri introdotti inoltre cresce con l'ordine dello sviluppo pertanto è necessario arrestarsi ad un ordine 2 o 4 al massimo, anche perché per potenze pari superiori si hanno coppie di zeri a parte reale negativa.

40) Approssimazione di Padè :

Consente di approssimare un polinomio con una funzione razionale fratta, scegliendo il grado del numeratore pari al grado del denominatore si trova per l'approssimazione di 1° ordine dell'esponenziale 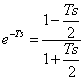mentre per l'approssimazione del 2° ordine 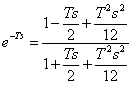si nota che in entrambe i casi si ottiene l'importante risultato di lasciare immutato l'eccesso poli-zeri ma nel caso di approssimazione del 1° ordine è necessario scambiare il luogo positivo con il luogo negativo.

41) Considerazioni sulla stabilità nel caso di sistemi a ritardi finiti :

Si tratta di sistemi sempre instabili, in quanto sono presenti degli zeri equivalenti che si trovano nel semipiano positivo e dato che al crescere di k il luogo si sposta dai poli a ciclo aperto verso gli zeri a ciclo aperto, si ha che necessariamente si và verso l'instabilità.

42) Relazione tra poli a ciclo aperto e poli a ciclo chiuso :

Una regola valida per sistemi con n-m ³ 2 afferma che la somma della posizione dei poli a ciclo aperto è uguale alla somma della posizione dei poli a ciclo chiuso.

43) Contorno delle radici :

Nel caso in cui in un sistema oltre al guadagno possa variare anche un altro parametro come la posizione a di un polo, si scrive l'equazione caratteristica fittizia ottenuta fissando k (normalmente pari ad 1) e raccogliendo i termini in a , si ottiene quindi da cui si può variare a e trovare il corrispondente luogo delle radici.