Statistica matematica
1) Stima per intervalli :
Si tratta di una stima avente l´obiettivo di individuare tra tutti i valori di c1 e c2 per i quali { c1 < X < c2 } = g , quello di lunghezza minima.
2) Verifica delle ipotesi statistiche :
È una branca della teoria della decisione basata sulla scelta tra 2 funzioni di distribuzioni di probabilità.
H0 detta ipotesi di base
H1 detta ipotesi alternativa
3) Spazio degli eventi :
È l´insieme degli eventi possibili tra i quali scegliere, è indicato con M .
4) Spazio dei segnali :
È l´insieme di tutte le possibili forme d´onda inviate all´osservatore, è indicato con S .
5) Spazio delle osservazioni :
È l´insieme di tutti i possibili segnali ricevuti, è indicato con Z .
6) Spazio delle decisioni :
È l´insieme di tutti i possibili risultati del processo di decisione, è indicato con D .
7) Regola di decisione :
Si tratta di una regola deterministica che associa ad ogni osservazione una decisione.
8) Errore di 1° tipo in una decisione binaria dopo singola osservazione :
Si ha un errore di 1° tipo se l´ipotesi H0 viene rigettata pur essendo vera.
9) Errore di 2° tipo in una decisione binaria dopo singola osservazione :
Si ha un errore di 2° tipo se l´ipotesi corretta è H1 ma i risultati della esperimento non supportano il rigetto di H0.
10) Criterio della massima verosimiglianza :
La regola di decisione sceglie l´evento che ha maggiore probabilità di aver causato l´osservazione.
11) Rapporto di verosimiglianza :
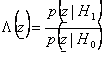
12) Criterio di Neyman - Person :
Individua una regola di decisione che minimizza b , avendo fissato a .
13) Differenza tra stima di parametro e verifica delle ipotesi :
La stima di parametro consente tramite le osservazioni su di un solo modello di stimarne uno o più parametri mentre la verifica delle ipotesi mette a confronto 2 modelli, quello della ipotesi nulla e quello della ipotesi alternativa.
Numeri casuali
14) Definizione operativa di numero casuale :
È una sequenza di numeri casuali risultanti da un esperimento fisico
15) Definizione concettuale di numero casuale :
È una sequenza di variabili aleatorie i.i.d.
16) Modalità per la generazione di numeri casuali :
a) tramite tabelle
b) tramite algoritmi congruenziali
17) Descrivere un generatore di numeri casuali ricorsivo :
Si parte da un valore iniziale e si ottiene il valore successivo in funzione del valore precedente.
18) Descrivere un generatore di numeri casuali congruenziale :
Si basa sul concetto di congruenza pertanto il valore attuale è legato al resto della divisione per m del valore precedente.
19) Metodo per generare numeri casuali con una data distribuzione tramite un calcolatore :
Occorre calcolare i valori della funzione F-1(u) per u = ui , essendo {ui} una sequenza di numeri casuali uniforme.
20) Descrivere il metodo Monte Carlo :
È basato su di un campionamento casuale ed utilizzato ad esempio per il calcolo di integrali, in pratica si effettua N volte un esperimento aleatorio e poi si calcola la media di tutti i risultati ottenuti.
Teoria della stima
21) Stima di punto :
Si tratta di una funzione della osservazione x essa è ![]() = g(x)
= g(x)
22) Stimatore :
Si tratta di una funzione del vettore X costituito da tutte le osservazioni x esso è ![]() = g(X)
= g(X)
23) Errore di stima :
È la differenza tra lo stimatore ed il parametro incognito q cioè e = ![]() - q
- q
24) Polarizzazione dello stimatore :
Si tratta del valor medio della errore di stima b(![]() ) = E(
) = E(![]() - q)
- q)
25) Varianza di uno stimatore :
È il valore atteso del quadrato della errore di stima V(![]() ) = E[ (
) = E[ (![]() - E(
- E(![]() ))2 ]
))2 ]
26) Stimatore consistente :
Uno stimatore è consistente se l´errore di stima tende a 0 per N che tende ad infinito.
27) Stimatore ottimo :
È lo stimatore che minimizza l´errore quadratico medio e = E[ (![]() - q)2 ]
- q)2 ]
28) Descrivere la stima per intervalli :
Vengono definite una coppia di funzioni della osservazione ![]() 1 = g 1 (X) e
1 = g 1 (X) e ![]() 2 = g 2 (X) i quali definiscono un intervallo all´interno del quale il parametro q è contenuto con una probabilità g.
2 = g 2 (X) i quali definiscono un intervallo all´interno del quale il parametro q è contenuto con una probabilità g.
29) Obiettivo della stima per intervalli :
Minimizzare la lunghezza della intervallo |![]() 1 -
1 - ![]() 2 | .
2 | .
