Campi elettrici e magnetici variabili nel tempo
1) Equazioni di Maxwell nel caso stazionario nel vuoto :
![]()
![]()
![]()
![]()
2) Legge di Faraday Neumann :
Intende descrivere fenomeni in cui una variazione nel tempo del flusso di B concatenato con il circuito induce in esso una f.e.m. data da ![]() . Le variazioni di flusso possono derivare da una delle seguenti cause :
. Le variazioni di flusso possono derivare da una delle seguenti cause :
a) spostamento meccanico del circuito
b) variazione del campo B nel tempo
c) variazione della geometria del circuito
3) Campo elettrico in condizioni non stazionarie :
In condizioni non stazionarie il campo elettrico non è più conservativo, non vale cioè più la ![]() bensì si trova una dipendenza dalla variazione temporale del campo B, così come si intuisce dalla legge di Faraday Neumann.
bensì si trova una dipendenza dalla variazione temporale del campo B, così come si intuisce dalla legge di Faraday Neumann.
4) Legge di Lenz :
La f.e.m. che si induce in un circuito a seguito della variazione del flusso di B concatenato è tale da opporsi a questa variazione di flusso, ossia scorrerà nel circuito una corrente indotta la quale dà luogo ad un campo B che si oppone a quello che l´ha generato.
5) Flusso tagliato :
Nel caso in cui B sia costante ed il circuito sia in movimento, il flusso tagliato è il flusso attraverso le pareti del cilindro che unisce il circuito al tempo t con il circuito al tempo t´ . Esso è pari alla variazione di flusso del circuito.
6) Causa della f.e.m. indotta nel caso di circuito in moto e sorgente ferma :
La forza di Lorentz.
7) Causa della f.e.m. indotta nel caso di circuito fermo e sorgente in moto :
È sempre la forza di Lorentz, basta scegliere un sistema di riferimento in movimento nel quale la sorgente sia ferma.
8) Terza equazione di Maxwell nel caso non stazionario :
![]()
Si ottiene dalla ![]() essendo
essendo ![]() su di questa si applica il teorema del rotore ed infine si eguagliano gli integrandi ai 2 membri.
su di questa si applica il teorema del rotore ed infine si eguagliano gli integrandi ai 2 membri.
9) f.e.m. autoindotta :
Un circuito percorso da corrente variabile nel tempo dà luogo ad un campo B anche esso variabile nel tempo , si avrà pertanto una variazione del flusso di B concatenato con il circuito stesso e quindi per la ![]() si indurrà una f.e.m. che si oppone a quella che l´ha generata.
si indurrà una f.e.m. che si oppone a quella che l´ha generata.
10) Coefficiente di autoinduzione :
È anche detto induttanza e risulta essere un coefficiente di proporzionalità tra il flusso di B attraverso il circuito e la corrente I che ha generato B , in formule si ha ![]() , si misura in Henry e dipende unicamente da caratteristiche geometriche.
, si misura in Henry e dipende unicamente da caratteristiche geometriche.
11) Coefficiente di autoinduzione di un solenoide :
![]()
12) Coefficiente di autoinduzione di una linea bifilare :
![]() essendo D la distanza tra i conduttori ed a il raggio di ognuno di essi
essendo D la distanza tra i conduttori ed a il raggio di ognuno di essi
13) Coefficiente di autoinduzione di un cavo coassiale :
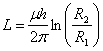
14) Costante di tempo del circuito LR :
![]()
15) Extracorrente di apertura :
Quando si apre un circuito in cui è presente una induttanza, la variazione della corrente e quindi del flusso è istantanea e quindi per la legge di Faraday Neumann si produrrà una f.e.m. autoindotta molto elevata che può anche arrivare a far scoccare una scintilla ai capi della interruttore.
16) Legge di Felici :
Stabilisce la carica Q che fluisce in un circuito come conseguenza di una variazione del flusso di B si ha ![]() .
.
17) Coefficiente di mutua induzione :
Quando si hanno 2 circuiti percorsi da corrente variabile nel tempo, ebbene la corrente che scorre in uno dei 2 produce un campo B che si concatena con la altro circuito dando luogo ad una f.e.m. indotta e quindi ad una corrente. In formule ![]() si ha inoltre
si ha inoltre ![]() .
.
18) Energia posseduta da una induttanza percorsa da corrente I :
![]() rappresenta l´energia posseduta da una induttanza percorsa da corrente I
rappresenta l´energia posseduta da una induttanza percorsa da corrente I
Si ottiene moltiplicando per Idt l´equazione differenziale di un circuito RL con generatore individuando la densità di energia LIdI ed integrandola tra 0 ed I.
19) Densità di energia in un campo magnetico :
![]()
Rappresenta la densità di energia presente in una regione di spazio in cui sia presente un campo di induzione magnetica di modulo B. Integrandola su di un volume si ottiene ![]() è quindi molto utili per calcolare induttanze laddove il metodo dei flussi sia di difficile applicazione.
è quindi molto utili per calcolare induttanze laddove il metodo dei flussi sia di difficile applicazione.
20) Correnti parassite o di Foucault :
Se in un conduttore si ha un campo B variabile nel tempo, eseguendo la circuitazione di E lungo un qualsiasi circuito chiuso essendo ![]() si trova un valore non nullo quindi all´interno del conduttore circolano correnti indotte parassite o di Foucault che sottraggono energia al campo magnetico.
si trova un valore non nullo quindi all´interno del conduttore circolano correnti indotte parassite o di Foucault che sottraggono energia al campo magnetico.
21) Densità di corrente di spostamento :
![]()
La corrente di spostamento viene introdotta per spiegare perché se si applica il teorema della circuitazione con una superficie che passa dentro il condensatore si ottiene un risultato diverso rispetto a quello che si avrebbe con una superficie che attraversa un filo del circuito che porta al condensatore.
22) Corrente di spostamento :
È il flusso attraverso una qualunque superficie S della corrente di spostamento ![]() .
.
23) Quarta equazione di Maxwell nel caso non stazionario :
Stabilisce la dipendenza del rotore di B anche dalla variazione temporale del campo elettrico.
![]()
Si ottiene sostituendo la ![]() nell´equazione di continuità
nell´equazione di continuità ![]()
24) Equazioni di Maxwell nel vuoto nel caso non stazionario :
![]()
![]()
![]()
![]()
25) Equazioni di Maxwell nella materia nel caso non stazionario :
![]()
![]()
![]()
![]()
