Teoremi sulle successioni e sulle serie di funzioni
Successioni di funzioni
1) Criterio di Convergenza puntuale :
Condizione necessaria e sufficiente perché la successione di funzioni fn converga puntualmente in A è che, fissato e > 0, " tÎA esista N(e,t) tale che : |fn(t) - fm(t)| < e " n, m > N .
2) Criterio di Convergenza uniforme :
Condizione necessaria e sufficiente perché la successione di funzioni fn converga uniformemente in A è che, fissato e > 0, esista N(e) tale che : |fn(t) - fm(t)| < e " tÎA " n, m > N .
3) Il limite di una successione di funzioni limitate fn convergente uniformemente è una funzione limitata :
Si parte dalla definizione della uniforme convergenza |fn(t) - fm(t)| < e se n, m > N dopodiché si manda n ad ¥ e si pone m = N. A questo punto si può utilizzare la disuguaglianza triangolare e scrivere |f(t)| - |fN(t)| < |f(t) - fN(t)| < e
Þ ponendo e = 1 si ha |f(t)| < 1 + |fN(t)| e quindi il sup del |f| è limitato dal sup di |fN|
4) Teorema dello scambio dei limiti
Sia ![]() uniformemente in A e
uniformemente in A e ![]() Þ
Þ ![]()
Dimostro prima che la successione ln a destra della uguale è convergente, troveremo che il suo limite è l e lo stesso limite si avrà anche per il 1° membro. La convergenza si stabilisce in base al criterio di convergenza uniforme, infatti si ha
|ln - lm| = |ln - fn(t) + fn(t) - fm(t) + fm(t) - lm| £ |ln - fn(t)| + |fn(t) - fm(t)| + |fm(t) - lm| < e essendo i moduli esterni minori di e per ![]() ed il modulo centrale minore di e per la convergenza uniforme in A. Rimane quindi solo da dimostrare che il 1° membro
ed il modulo centrale minore di e per la convergenza uniforme in A. Rimane quindi solo da dimostrare che il 1° membro ![]() per far ciò impostiamo la consueta disuguaglianza dei limiti cioè |f(t) - l| £ |f(t) - fN(t)| + |fN(t) - lN(t)| + |lN(t) - l| £ 2e + |fN(t) - lN| < 3e , dove per gli esterni si è sfruttata la convergenza uniforme della ln e per il termine centrale la 2ª ipotesi del teorema.
per far ciò impostiamo la consueta disuguaglianza dei limiti cioè |f(t) - l| £ |f(t) - fN(t)| + |fN(t) - lN(t)| + |lN(t) - l| £ 2e + |fN(t) - lN| < 3e , dove per gli esterni si è sfruttata la convergenza uniforme della ln e per il termine centrale la 2ª ipotesi del teorema.
5) Se la successione di funzioni continue fn converge uniformemente Þ il suo limite f è una funzione continua.
Si dimostra applicando il teorema dello scambio dei limiti alla funzione ![]() .
.
6) Teorema dello scambio del limite con la derivata :
Si abbia una successione di funzioni fn : A®Â derivabili e
a) la successione delle derivate {fn´} converge uniformemente in (a,b) con limite g
b) la successione delle funzioni {fn} converge almeno in un punto t0 Î (a,b)
Þ anche la successione fn converge uniformemente in (a,b) e si ha ![]()
a) Si deve dimostrare che {fn} converge uniformemente, ossia è rispettata la condizione necessaria e sufficiente di convergenza |fn(t) - fm(t)| < e a tal fine si applica il teorema di Lagrange ![]() da cui sfruttando la convergenza puntuale in t0 e l´uniforme convergenza della successione delle derivate {fn´} si stabilisce l´uniforme convergenza ad f(t) della successione {fn }.
da cui sfruttando la convergenza puntuale in t0 e l´uniforme convergenza della successione delle derivate {fn´} si stabilisce l´uniforme convergenza ad f(t) della successione {fn }.
b) Supponiamo che {fn(t)} converga uniformemente ad f(t) mostro che f è derivabile, si ha : ![]() da cui essendo il rapporto incrementale derivabile come si ottiene applicando ancora Lagrange e la convergenza uniforme della serie delle derivate, si possono scambiare i due limiti ottenendo
da cui essendo il rapporto incrementale derivabile come si ottiene applicando ancora Lagrange e la convergenza uniforme della serie delle derivate, si possono scambiare i due limiti ottenendo ![]() da cui la tesi.
da cui la tesi.
7) Teorema dello scambio del limite con l´integrale :
Si abbia una successione fn di funzioni limitate integrabili sull´intervallo [a,b] , convergente uniformemente con limite f
Þ ![]()
Si ha ![]() in quanto la successione fn converge uniformemente ad f . Si deve solo dimostrare l´integrabilità di f la quale si fa in termini di suddivisioni sfruttando l´uniforme convergenza di fn ad f .
in quanto la successione fn converge uniformemente ad f . Si deve solo dimostrare l´integrabilità di f la quale si fa in termini di suddivisioni sfruttando l´uniforme convergenza di fn ad f .
Serie di funzioni
8) Criterio di Convergenza puntuale di Cauchy :
Condizione necessaria e sufficiente perché la serie di funzioni Sxn(t) converga puntualmente in A è che, fissato e > 0,
" tÎA esista N(e,t) tale che : |xp(t)+ xp+1(t)+ ... + xp+q(t)| < e se n, m > N .
9) Criterio di Convergenza uniforme :
Condizione necessaria e sufficiente perché la serie di funzioni Sxn(t) converga uniformemente in A è che, fissato e > 0, esista N(e) tale che : |xp(t)+ xp+1(t)+ ... + xp+q(t)| < e " tÎA se n, m > N .
10) Criterio di Weierstrass :
Data la successione di funzioni xn ed una serie convergente di costanti positive Scn e definitivamente si ha |xn(t)| £ cn
Þ la serie di funzioni Sxn(t) converge uniformemente in A.
Si dimostra in virtù della disuguaglianza triangolare e del criterio di convergenza di Cauchy dal quale deriva
|xp(t)+ xp+1(t)+ ... + xp+q(t)| < |xp(t)| + |xp+1(t)| + ... + |xp+q(t)| < cp + cp+1 + ... + cp+q < e
11) Teorema della convergenza totale :
Se {xn} è una successione a valori in uno spazio di Banach (normato e completo) la cui serie delle norme S||xn || è convergente Þ converge anche la serie Sxn .
La dimostrazione ricalca quanto già ricavato per la convergenza assoluta delle serie numeriche, sfruttando analogamente il Criterio di convergenza puntuale di Cauchy e la disuguaglianza triangolare. Il teorema è detto della convergenza totale in quanto una serie per la quale converge la serie delle norme è detta totalmente convergente.
12) Teorema del limite di una serie :
Se Sfn(t) è una serie di funzioni uniformemente convergente con somma F(t) ed esiste il limite ![]()
Þ la serie Sln converge e si ha ![]()
13) La somma di una serie uniformemente convergente di funzioni continue è una funzione continua.
Si deve dimostrare la continuità della somma della serie che ricordiamo essere pari alla somma del resto n-esimo e della somma parziale n-esima, considerando l´incremento h si hanno le due seguenti uguaglianze :
![]() e
e ![]() sottraendo membro a membro si ottiene :
sottraendo membro a membro si ottiene :
![]()
Dove per la 1ª quadra si sfrutta che Sn(x) è somma di funzioni continue e pertanto continua mentre per la 2ª e la 3ª quadra si sfrutta che la serie è uniformemente convergente quindi il resto n-esimo può essere reso piccolo quanto si vuole.
14) Teorema della integrale di una serie :
Si abbia una successione fn di funzioni limitate integrabili sull´intervallo [a,b] , se la serie Sfn(t) converge uniformemente in (a,b) con somma F(t) Þ F è integrabile e si ha ![]()
Si ricorda che la somma di una serie S è pari alla somma parziale n-esima Sn(x) più il resto n-esimo Rn(x) , integrando e passando ai moduli si ha : ![]()
dove si è sfruttata la convergenza uniforme della serie. Pertanto il teorema è dimostrato.
15) Teorema della derivata di una serie :
Si abbia una successione fn di funzioni derivabili e
a) la serie delle derivate Sfn´ converge uniformemente in (a,b) con somma G(t)
b) la serie delle funzioni Sfn converge almeno in un punto t0 Î (a,b)
Þ anche la serie Sfn converge uniformemente in (a,b) e si ha ![]()
Sia g(x) =Sfn´ essendo uniformemente convergente per il teorema precedente può essere integrata termine a termine
![]() dove nell´ultimo passaggio si è sfruttata la convergenza alla sua somma della serie di funzioni. Derivando la precedente espressione si ottiene g(x) = S´(x) e dunque in definitiva S´(x) = Sfn´ .
dove nell´ultimo passaggio si è sfruttata la convergenza alla sua somma della serie di funzioni. Derivando la precedente espressione si ottiene g(x) = S´(x) e dunque in definitiva S´(x) = Sfn´ .
Serie di potenze
16) Se una serie di potenze ![]() converge uniformemente in un punto z0 Î C
converge uniformemente in un punto z0 Î C
Þ converge assolutamente in ogni punto tale che |z| < |z0|
Si ottiene per confronto con la serie geometrica infatti si ha 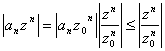 dove si è sfruttata la convergenza nel punto z0 per maggiorare con 1 il termine
dove si è sfruttata la convergenza nel punto z0 per maggiorare con 1 il termine ![]() . L´ultima serie è geometrica e converge Û |z| < |z0| nel qual caso il rapporto è minore di uno allora per il teorema del confronto anche
. L´ultima serie è geometrica e converge Û |z| < |z0| nel qual caso il rapporto è minore di uno allora per il teorema del confronto anche ![]() è assolutamente convergente.
è assolutamente convergente.
17) Criterio della radice per determinare il raggio di convergenza :
Data la serie ![]() sia
sia ![]() Þ r = 1/l è il raggio di convergenza :
Þ r = 1/l è il raggio di convergenza :
18) Criterio del rapporto per determinare il raggio di convergenza :
Data la serie ![]() se esiste il limite
se esiste il limite 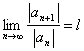 Þ r = 1/l è il raggio di convergenza :
Þ r = 1/l è il raggio di convergenza :
19) Proprietà della somma di una serie di potenze :
a) La serie converge uniformemente in ogni cerchio : |z| £ r´ con r´ < r
b) La somma della serie è una funzione continua in |z| < r
c) La serie delle derivate è ancora una serie di potenze che ha lo stesso raggio di convergenza
d) La somma della serie è derivabile in senso complesso con derivata continua in |z| < r ; la sua derivata è pari alla somma della serie delle derivate
a) Si dimostra mediante il teorema di Weierstrass infatti la serie converge assolutamente per z = r´ essendo esso interno al raggio di convergenza e situato sulla asse reale pertanto abbiamo trovato una serie di costanti positive Sanr´ che converge e che maggiora la nostra serie Sanzn che pertanto converge assolutamente.
b) Ricordando che la somma f(z) di una serie uniformemente convergente di funzioni continue è continua e data l´uniforme convergenza di Sanzn appena dimostrata e la arbitrarietà del punto r´ , il teorema risulta dimostrato.
c) Si ha ![]() che è una serie di potenze con coefficienti bn =(n+1)an+1 , applicando il criterio della radice si ottiene
che è una serie di potenze con coefficienti bn =(n+1)an+1 , applicando il criterio della radice si ottiene ![]() e quindi il raggio di convergenza è lo stesso di an .
e quindi il raggio di convergenza è lo stesso di an .
d) E´ sufficiente scrivere fx e fy e verificare che soddisfano le relazioni di Cauchy - Riemann.
20) Altre proprietà della somma di una serie di potenze :
a) La somma della serie di potenze è di classe C¥ in |z| < r
b) La derivata k-esima della somma della serie è pari alla somma della serie delle derivate k-esime.
c) Tra i coefficienti della serie e le derivate della somma f(z) sussiste la relazione ![]()
a) Segue dal fatto che la serie delle derivate è ancora una serie di potenze con lo stesso raggio di convergenza.
b) E´ esattamente il punto d) del teorema 19)
c) Si ottiene in maniera pratica derivando la somma della serie
21) Teorema di Abel :
Se una serie di potenze Sanzn converge in uno dei punti estremi del suo intervallo di convergenza
Þ L´intervallo di convergenza include anche questo punto.
L´uniforme convergenza si ha se si dimostra che il resto n-esimo è minore di e ![]()
essendo ![]() si può scrivere
si può scrivere ![]() da cui raccogliendo xn si ha
da cui raccogliendo xn si ha ![]() si può quindi sfruttare l´uniforme convergenza che rende tutti i resti n-esimi minori di e / 2 raccogliendo i quali rimane dentro parentesi lo sviluppo della serie geometrica per la quale la somma è
si può quindi sfruttare l´uniforme convergenza che rende tutti i resti n-esimi minori di e / 2 raccogliendo i quali rimane dentro parentesi lo sviluppo della serie geometrica per la quale la somma è ![]() semplificando si ottiene che il resto n-esimo è minore di e .
semplificando si ottiene che il resto n-esimo è minore di e .
22) Condizione necessaria per la sviluppabilità in serie di Taylor di una funzione f :
Sia f Î C¥ (-r , r) ed esista una costante M, indipendente da n e da x tale che si abbia, definitivamente ![]() Þ f è sviluppabile in serie di taylor in (-r , r).
Þ f è sviluppabile in serie di taylor in (-r , r).
Si sostituisce la condizione nel resto n-esimo ![]() ottenendo
ottenendo  che tende a 0 per n che tende ad ¥.
che tende a 0 per n che tende ad ¥.
