Teoremi sulle serie numeriche
Criteri di convergenza
1) Criterio di Cauchy
La serie ![]() è convergente Û " e >0 $ N tale che
è convergente Û " e >0 $ N tale che ![]() per ogni n > m , m ³ 0 ossia se il resto parziale è minore di e .
per ogni n > m , m ³ 0 ossia se il resto parziale è minore di e .
2) Corollario del Criterio di Cauchy:
Condizione necessaria affinché la serie ![]() converga è che
converga è che ![]()
Si ottiene dal Criterio di Cauchy ponendo m = 0 ed osservando che " n > N deve essere |an| < e .
Criteri di convergenza per le serie a termini non negativi
3) Criterio del confronto :
Se le serie ![]() e
e![]() sono entrambe a termini non negativi e se an £ bn " n ³0 Û
sono entrambe a termini non negativi e se an £ bn " n ³0 Û
a) Se la serie ![]() è convergente , allora lo è anche la serie
è convergente , allora lo è anche la serie ![]()
b) Se la serie ![]() è divergente , allora lo è anche la serie
è divergente , allora lo è anche la serie ![]()
c) Per il criterio di Cauchy, essendo bn convergente, si ha ![]() allora essendo " n an < bn , segue che è anche
allora essendo " n an < bn , segue che è anche ![]() quindi per lo stesso criterio di Cauchy la serie
quindi per lo stesso criterio di Cauchy la serie ![]() è convergente anche essa.
è convergente anche essa.
4) Corollario del Criterio del confronto
Se le serie ![]() e
e![]() sono entrambe a termini positivi e an ~ bn Þ le 2 serie avranno lo stesso carattere.
sono entrambe a termini positivi e an ~ bn Þ le 2 serie avranno lo stesso carattere.
Ricordando che 2 serie sono asintotiche se ![]() e quindi si può dire che an è compreso tra 0.5 bn e 1,5 bn e quindi se ad esempio bn diverge, dovrà divergere anche an .
e quindi si può dire che an è compreso tra 0.5 bn e 1,5 bn e quindi se ad esempio bn diverge, dovrà divergere anche an .
5) Criterio della radice
Se![]() è una serie a termini non negativi Þ se esiste 0 £ l < 1 ed un N tale che " n> N si ha
è una serie a termini non negativi Þ se esiste 0 £ l < 1 ed un N tale che " n> N si ha ![]()
Þ la serie è convergente
Si dimostra osservando che per n ³ N deve essere an £ ln e quindi la serie converge in quanto è una serie geometrica di ragione l < 1.
6) Corollario del Criterio della radice
Se![]() è una serie a termini non negativi Þ se esiste il limite
è una serie a termini non negativi Þ se esiste il limite ![]() Þ
Þ
a) la serie è convergente se l < 1
b) la serie è divergente se l > 1
7) Criterio di Raabe :
Se 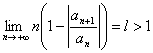 Þ la serie
Þ la serie![]() converge assolutamente.
converge assolutamente.
8) Criterio del rapporto :
Se![]() è una serie a termini positivi ed esiste 0 < l < 1 tale che
è una serie a termini positivi ed esiste 0 < l < 1 tale che ![]() Þ la serie è convergente
Þ la serie è convergente
Si ricava per induzione, se supponiamo ![]() per ogni n si ha che a1 £ l a0 , a2 £ l a1 £ l (l a0) e così via quindi si avrà an £ ln a0 quindi osservando che la serie Sln a0 ha lo stesso carattere della serie Sln la quale converge essendo la serie geometrica ed l<1 , ne segue che converge anche S an .
per ogni n si ha che a1 £ l a0 , a2 £ l a1 £ l (l a0) e così via quindi si avrà an £ ln a0 quindi osservando che la serie Sln a0 ha lo stesso carattere della serie Sln la quale converge essendo la serie geometrica ed l<1 , ne segue che converge anche S an .
9) Corollario del Criterio del rapporto
Se![]() è una serie a termini positivi ed esiste il limite
è una serie a termini positivi ed esiste il limite ![]() Û
Û
a) la serie è convergente se l < 1
b) la serie è divergente se l > 1
10) Criterio integrale :
Se f(x) è una funzione positiva, continua e decrescente per x ³ N e tale che f(n) = an ed inoltre esiste finito ![]()
Þ ![]() converge .
converge .
Per la monotonia si ha an+1 = f(n+1) £ f(x) £ f(n) = an pertanto integrando tra n ed n+1 e sfruttando che sulle ascisse il passo è quello dei numeri naturali cioè 1 si ha an+1 £ ![]() £ an e sommando gli intervallini
£ an e sommando gli intervallini
a2 + a3 + ... + am £ ![]() £ a1 + a2 + a3 + ... + am . Ne consegue che se l´integrale converge allora la somma a sinistra sarà crescente e limitata superiormente e pertanto ammetterà limite.
£ a1 + a2 + a3 + ... + am . Ne consegue che se l´integrale converge allora la somma a sinistra sarà crescente e limitata superiormente e pertanto ammetterà limite.
11) Criterio di condensazione
Se {an} è una successione a termini non negativi e decrescenti allora ![]() converge Û converge la serie
converge Û converge la serie ![]()
Criteri di convergenza per le serie a termini con segno randomico
12) Se la serie ![]() è convergente Þ la serie
è convergente Þ la serie ![]() è convergente.
è convergente.
Se ![]() converge vuol dire che per il Criterio di Cauchy esiste un N : " n, m > N si ha | an | + |an+1| + ... + |an+m| < e del resto per la disuguaglianza triangolare è anche | an + an+1 + ... + an+m| < | an | + |an+1| + ... + |an+m| < e e pertanto lo stesso Criterio di Cauchy ci dice che anche la serie
converge vuol dire che per il Criterio di Cauchy esiste un N : " n, m > N si ha | an | + |an+1| + ... + |an+m| < e del resto per la disuguaglianza triangolare è anche | an + an+1 + ... + an+m| < | an | + |an+1| + ... + |an+m| < e e pertanto lo stesso Criterio di Cauchy ci dice che anche la serie ![]() converge.
converge.
Criteri di convergenza per le serie a termini con segno alternato
13) Criterio di Leibniz :
La serie ![]() con an > 0 "n è convergente a patto che :
con an > 0 "n è convergente a patto che :
a) La successione an è decrescente b) ![]()
Il termine generico della serie è sn = a0 - a1 + a2 - .... (-1)nan (dove chiaramente i termini pari si sommano ed i termini dispari si sottraggono) si può osservare che le ridotte pari sono decrescenti infatti s2n+2 = s2n - (a2n+1 -a2n+2) £ s2n dove si utilizza il fatto che {an} è decrescente quindi il penultimo termine prevale sull´ultimo. Al contrario invece le ridotte dispari sono crescenti infatti s2n+1 = s2n -1 + (a2n -a2n+1) ³ s2n - 1 .
Essendo inoltre s2n+1 = s2n - a2n+1 ed il termine generico an > 0 se ne deduce che s2n ³ s2n+1 ³ s2n-1 ³ ... .³ s1 dove si è sfruttata la decrescenza appena dimostrata quindi la successione delle ridotte pari è decrescente e limitata inferiormente pertanto converge, supponiamo ad S, ebbene anche la successione delle ridotte dispari converge ad S infatti riprendendo la s2n+1 = s2n - a2n+1 e sfruttando b) si deduce che per n®+¥ si ha s2n+1 = s2n .
14) Criterio di Abel - Dirichlet :
Se {an} è una successione a valori complessi le cui ridotte n-esime sono tutte limitate e {bn} è una successione a valori reali che tende monotonamente a 0, Þ La serie ![]() è convergente.
è convergente.
Si può maggiorare ![]() dove il secondo membro non è altro che la formula di sommazione per parti analoga alla integrazione per parti. Ricordando che le ridotte n-esime An sono tutte in modulo minori di M e che {bn } è una successione decrescente segue che
dove il secondo membro non è altro che la formula di sommazione per parti analoga alla integrazione per parti. Ricordando che le ridotte n-esime An sono tutte in modulo minori di M e che {bn } è una successione decrescente segue che ![]() da cui sviluppando la sommatoria si ha = 2 bp M < 2 e M pertanto per la arbitrarietà di e ed il Criterio di Cauchy segue che la serie
da cui sviluppando la sommatoria si ha = 2 bp M < 2 e M pertanto per la arbitrarietà di e ed il Criterio di Cauchy segue che la serie ![]() è convergente.
è convergente.
Operazioni sulle serie
15) Prodotto di una serie per un numero :
![]() :=
:=![]() inoltre la serie
inoltre la serie ![]() ha lo stesso carattere della serie
ha lo stesso carattere della serie ![]()
16) Somma di 2 serie :
![]() +
+![]() :=
:=![]() e se entrambe le serie sono convergenti allora lo è anche la serie somma.
e se entrambe le serie sono convergenti allora lo è anche la serie somma.
17) Prodotto (secondo Cauchy) di 2 serie :
![]() *
*![]() :=
:=![]() essendo
essendo ![]()
18) Teorema di Mertens riguardante il prodotto (secondo Cauchy) di 2 serie :
Se![]() e
e![]() sono 2 serie convergenti ed una delle 2 è anche assolutamente convergente allora la serie prodotto
sono 2 serie convergenti ed una delle 2 è anche assolutamente convergente allora la serie prodotto![]() è convergente con somma C=AB
è convergente con somma C=AB
Proprietà associative e commutative riguardanti le serie
19) Per serie convergenti o divergenti vale la proprietà associativa ossia se si crea una serie Sbn di cui ogni termine è somma di alcuni di San , Þ le due serie hanno lo stesso carattere.
20) Se San è una serie assolutamente convergente allora ogni suo riordinamento è anche assolutamente convergente ed ha la stessa somma.
