Teoremi sulle funzioni implicite
1) Teorema di Dini :
Sia g : A® Â , A aperto di Â2 . Supponiamo che :
a) g e gy siano continue in A.
b) nel punto x0 , y0 Î A si abbia g(x0 , y0) = 0 e gy (x0 , y0) ¹ 0 .
Þ esistono un intorno U di x0 ed un´unica funzione f : U®Â , continua in U, tale che y0 = f(x0) e che g(x,f(x)) = 0 per ogni x Î U.
Se inoltre gx è continua in A Þ f è derivabile in U e vale la formula ![]() " x Î U .
" x Î U .
Lo scopo è quello di riportarsi a poter applicare il teorema degli zeri su un opportuno intervallo (Se una funzione continua definita su di un intervallo [a,b] assume ai suoi estremi valori non nulli e di segno opposto, allora f ammette almeno uno zero y Î (a,b) ) Per l´individuazione della intervallo si applica il teorema della permanenza del segno alla gy che supporremmo positiva gy (x0 , y0) > 0 (se ![]() allora f(x) > 0 definitivamente per x ® x0 dove il termine definitivamente indica che la proprietà è valida per ogni x appartenente ad almeno un intorno di x0 con x ¹ x0 .)
allora f(x) > 0 definitivamente per x ® x0 dove il termine definitivamente indica che la proprietà è valida per ogni x appartenente ad almeno un intorno di x0 con x ¹ x0 .)
pertanto la funzione della sola y g(x0 ,y) è strettamente crescente e dato che g(x0 , y0) = 0 necessariamente sarà
g(x0 , y0 - b) < 0 e g(x0 , y0 + b) > 0 , inoltre relazioni analoghe valgono non solo in x0 bensì anche in una fascia
[x0 - d , x0 + d]. A questo punto scegliendo un x appartenente a questa fascia per il teorema degli zeri dovrà esistere un y tale che g(x , y) = 0 sostituendo e = b si ottiene che f è continua nella fascia [x0 - d , x0 + d].
Per dimostrare la formula si utilizza il teorema del valor medio (Se f è continua in [a,b] e derivabile in (a,b) Þ esiste un punto c tale che ![]() ) si ha pertanto g(x,y) - g(x,y) = 0 = gx(x,h)(x-x) + gy(x,h)(y-y)
) si ha pertanto g(x,y) - g(x,y) = 0 = gx(x,h)(x-x) + gy(x,h)(y-y)
da cui si ottiene 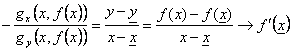 .
.
2) Teorema di Dini in più di 2 variabili :
Sia g : A® Â , A aperto di Ân+1 . Supponiamo che :
a) g e gy siano continue in A.
b) nel punto x0 , y0 Î A si abbia g(x0 , y0) = 0 e gy (x0 , y0) ¹ 0 .
Þ esistono un intorno U di x0 ed un´unica funzione f : U®Â , continua in U, tale che y0 = f(x0) e che g(x , f(x)) = 0 per ogni x Î U.
Se inoltre gx1 , .. , gxn sono continue in A Þ f è derivabile in U e vale la formula 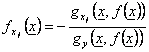 " x Î U
" x Î U
Dimostrazione analoga a quella che si ha nel caso tridimensionale.
3) Teorema di Dini per sistemi :
Sia g : A® Âm , A aperto di Âm+n . Supponiamo che :
a) g sia derivabile in A.
b) nel punto (x0 , y0) Î A si abbia g(x0 , y0) = 0 e det Dyg (x0 , y0) ¹ 0 .
Þ esistono un intorno V di x0 ed un´unica funzione y = f(x) tale che f è derivabile in V ed y0 = f(x0) e che g(x , f(x)) = 0 per ogni x Î V. Inoltre vale la formula ![]() .
.
Essendo : 
4) Teorema di Lagrange :
Siano f,g derivabili in un aperto X di Â2 e sia (x0 , y0) un punto regolare per E0 = {(x,y) Î Â2 : g(x,y)=0}
Þ (x0 , y0) è un punto critico vincolato ad E0 Û $ un numero reale l tale che Ñf(x0 , y0) = l Ñg(x0 , y0)
Þ Trattandosi di un punto critico vincolato (un punto regolare per il quale si annulla la derivata di f in direzione tangente al vincolo) il gradiente di f dovrà essere normale alla tangente così come del resto deve accadere per il vettore gradiente di g.
Ü Dalla equazione segue che il gradiente di f è normale all´insieme E0 nel punto (x0 , y0) e pertanto il punto è critico vincolato.
5) Metodo dei moltiplicatori di Lagrange :
a) occorre individuare i punti singolari del vincolo. Basta impostare il determinante Jacobiano ed imporre che esso sia nullo.
b) si individuano gli estremi liberi della lagrangiana.
c) La natura dei punti estremanti si ottiene dallo studio delle derivate della funzione implicita le quali si ricavano o tramite il teorema di Dini o tramite la derivata simbolica di funzione composta.
