Definizioni di Analisi 2
Serie
1) Serie :
Si tratta di una successione {sn}nella quale l´elemento di ordine n è pari alla somma dei primi n termini di una successione {an}. Ad esempio il 3° elemento della serie è la somma dei primi 3 termini della successione {an} , a0 + a1 + a2 .
2) Somma parziale n-esima o ridotta n-esima sn :
Si tratta del singolo elemento della successione {sn } ossia della somma dei primi n termini della successione {an }.
3) Serie di termini an :
Si indica ![]() = a0 + a1 + a2 + ...... + an .
= a0 + a1 + a2 + ...... + an .
4) Somma della serie :
Si tratta del valore del termine n-esimo della successione {sn} per n®+¥ nel caso che tale valore sia finito ![]() ossia nel caso che la serie converge.
ossia nel caso che la serie converge.
5) Resto della serie :
Il resto n-esimo della serie ![]() è
è ![]() e nel caso che la serie converge ad A , si ha
e nel caso che la serie converge ad A , si ha ![]() = Rn = A - sn .
= Rn = A - sn .
6) Carattere della serie :
Si tratta delle caratteristiche della somma dei termini per n®+¥ , essa può essere convergente, divergente o irregolare.
7) Serie geometrica di ragione q : ![]() converge a
converge a ![]() se |q| < 1.
se |q| < 1.
8) Serie di Mengoli : ![]() converge a
converge a ![]()
9) Serie Telescopiche : ![]() converge a a0 -
converge a a0 -![]()
10) Serie Armonica : ![]() diverge
diverge
11) Quando la serie an è assolutamente convergente ?
![]() è assolutamente convergente se la serie impostata col modulo
è assolutamente convergente se la serie impostata col modulo ![]() è convergente nel qual caso anche
è convergente nel qual caso anche ![]() converge mentre non è sempre vero il contrario.
converge mentre non è sempre vero il contrario.
12) Quando la serie ![]() è condizionatamente convergente ?
è condizionatamente convergente ?
Quando ![]() è convergente ma
è convergente ma ![]() non è convergente.
non è convergente.
13) Quando la serie ![]() è un riordinamento della serie
è un riordinamento della serie![]() ?
?
Quando esiste una applicazione biiettiva j tale che bn = a j (n) .
Spazi funzionali
14) Successione fondamentale o di Cauchy :
Una successione {an} a valori reali si dice fondamentale o di Cauchy se "e>0 esiste un NÎÀ tale che |an-am| <e per ogni coppia n, m > N.
15) Spazio metrico completo :
È uno spazio metrico in cui ogni successione fondamentale è convergente.
16) Convergenza puntuale :
Una successione di funzioni fn : A®Â si dirà convergente in A, con limite f : A®Â se, fissato e > 0 " tÎA , $
N = N(e,t) tale che |fn(t) - f(t)| < e se n > N.
17) Convergenza uniforme :
Una successione di funzioni fn : A®Â si dirà convergente uniformemente in A, con limite f : A®Â se, fissato e > 0
$ N = N(e) tale che |fn(t) - f(t)| < e se n > N.
18) Criterio di convergenza di Cauchy o di convergenza puntuale :
Condizione necessaria e sufficiente perché la successione di funzioni fn : A®Â converga puntualmente in A è che fissato e > 0 , " tÎA , $ N = N(e,t) tale che |fn(t) - fm(t)| < e " tÎA se n , m > N.
19) Criterio di convergenza uniforme :
Condizione necessaria e sufficiente perché la successione di funzioni fn : A®Â converga uniformemente in A è che fissato e > 0 $ N = N(e) tale che |fn(t) - fm(t)| < e " tÎA se n , m > N.
20) Applicazione Lipschitziana :
Sia (X,d) uno spazio metrico, un´applicazione F:X®X si dice lipschitziana se esiste un numero r > 0 tale che , " coppia x,y di punti di X si abbia d(F(x),F(y)) £ rd(x,y).
21) Spazio di Hilbert :
È uno spazio metrico (su esso è definita una distanza) e completo.
22) Funzioni ortogonali :
2 funzioni si dicono ortogonali se il loro prodotto scalare è nullo.
Serie di funzioni
23) Criterio di convergenza di Cauchy o di convergenza puntuale :
La serie ![]() di funzioni : A®Â converge puntualmente in A Û fissato e > 0 , " tÎA si può determinare un indice N =N(e,t) : " p ³N e " q ³ 0 si abbia |xp(t)+ xp+1(t)+ ....+ xp+q(t)| < e .
di funzioni : A®Â converge puntualmente in A Û fissato e > 0 , " tÎA si può determinare un indice N =N(e,t) : " p ³N e " q ³ 0 si abbia |xp(t)+ xp+1(t)+ ....+ xp+q(t)| < e .
La convergenza sarà uniforme Û $ N = N(e) tale che |xp(t)+ xp+1(t)+ ....+ xp+q(t)| < e " tÎA " p ³ N " q ³ 0.
24) Corollario del criterio di Cauchy :
Se ![]() converge puntualmente (uniformemente) in A Þ
converge puntualmente (uniformemente) in A Þ ![]() ® 0 puntualmente (uniformemente) in A.
® 0 puntualmente (uniformemente) in A.
25) Serie totalmente convergente:
È una serie per la quale converge la serie delle norme.
Serie di potenze
26) Espressione della serie di potenze : ![]()
![]()
27) Cerchio e raggio di convergenza :
Datosi che la serie converge in z0 Þ converge anche in |z| < |z0| che è un cerchio centrato nell´origine e di raggio
r := Sup{r : R < |z0|} , tale cerchio e tale raggio sono detti di convergenza.
28) Limite superiore o massimo limite :
È il massimo dei valori limite, è +¥ se la successione non è limitata superiormente.
29) Limite inferiore o minimo limite :
È il minimo dei valori limite, è +¥ se la successione non è limitata inferiormente.
Serie di Taylor
30) Serie di Taylor :
![]()
31) Funzione analitica :
Una funzione si dice analitica nel punto x0 ÎA se è sviluppabile in serie di Taylor in un intorno di x0 .
Serie di Fourier
32) Serie trigonometrica :
Si tratta della serie ![]()
33) Valore dei coefficienti della serie di Fourier :
![]()
![]()
34) Funzione continua a tratti :
Si tratta di una funzione continua su [a,b] tranne al più un n° finito di punti nei quali esistono finiti i limiti destro e sinistro e pertanto vi è una discontinuità di 1ª specie.
35) Quando f Î C2p :
f è periodica con periodo 2p ed è continua a tratti.
36) Condizione di Dirichlet :
Una funzione soddisfa nel punto x0 la condizione D di Dirichlet se verifica almeno una delle seguenti :
a) è derivabile in x0
b) è continua in x0 e dotata di derivata destra e sinistra in x0
c) ha una discontinuità di 1ª specie in x0 ed esistono finiti i limiti ![]() e
e ![]()
37) Tipologie di convergenza ad f delle serie di Fourier :
a) In media quadratica
b) Convergenza puntuale
c) Convergenza uniforme
38) Spazio di Hilbert :
X è uno spazio lineare con prodotto scalare <f,g> =![]() ed è completo rispetto alla norma indotta.
ed è completo rispetto alla norma indotta.
Equazioni differenziali
39) Equazione differenziale :
È una funzione che implica una funzione incognita e le sue derivate.
40) Ordine di una equazione differenziale :
È l´ordine della derivata di massimo ordine che compare nell´equazione.
41) Grado di una equazione differenziale :
È l´esponente della massima potenza della derivata del massimo ordine che compare nell´equazione.
42) Equazione differenziale ordinaria :
È una equazione in cui la funzione incognita dipende da una sola variabile indipendente.
43) Equazione differenziale alle derivate parziali :
È una equazione in cui la funzione incognita dipende da una o più variabili indipendenti.
44) Equazione differenziale in forma normale :
È una equazione in cui si può esplicitare la derivata di ordine massimo.
45) Soluzione di una equazione differenziale :
Sia f :D®Ân una funzione continua su di un aperto D di Ân+1 , allora una funzione y : I®Â di classe C´[I] tale che (t,y(t)) Î D e tÎ I è detta soluzione della equazione differenziale y´(t) = f(t,y(t)) a patto che la soddisfi identicamente
" tÎI essendo I un intervallo non degenere.
46) Soluzione generale di una equazione differenziale :
È l´insieme di tutte le soluzioni particolari della equazione differenziale.
47) Problema di Cauchy :
È un sistema costituito da un´equazione differenziale ed una o più condizioni iniziali che assegnano alla funzione incognita un dato valore all´istante t. Una volta individuato l´integrale generale si può determinare la soluzione particolare sostituendo le condizioni iniziali.
48) Funzione Lipschitziana :
L´applicazione f(t,y) è lipschitziana in D rispetto ad y, uniformemente in t, se esiste una costante L detta costante di Lipschitz tale che ||f(t,y)-f(t,z)|| £ L ||y-z|| per ogni coppia di punti (t,y) e (t,z). in D.
49) Funzione localmente Lipschitziana :
F(t,y) è localmente lipschitziana in D rispetto ad y, uniformemente in t, se ogni punto di D possiede un intorno nel quale esiste una costante L detta costante di Lipschitz tale che ||f(t,y)-f(t,z)|| £ L ||y-z|| per ogni coppia di punti (t,y) , (t,z) appartenenti all´intorno. La differenza rispetto alla precedente è quindi soltanto che L può dipendere dall´intorno.
50) Successione fondamentale o di Cauchy :
Una successione è fondamentale se " e >0 esiste un N tale che presi 2 qualsiasi elementi n ed m maggiori di N nel dominio della successione si ha che | an - am | < e
51) Spazio metrico completo :
Uno spazio metrico è deto completo se ogni successione in esso definita converge ad un punto dello spazio stesso.
52) Contrazione:
È una applicazione lipschitziana ove 0 < L < 1.
53) Punto fisso :
È un punto che viene trasformato in se stesso dalla applicazione.
54) Spazio di Banach :
È uno spazio normato e completo (Ogni successione fondamentale è convergente).
55) Integrale generale di una equazione scalare di ordine N :
Si consideri ![]() ove f : (a,b) x Ân ®Â è continua e globalmente lipschitziana Þ
ove f : (a,b) x Ân ®Â è continua e globalmente lipschitziana Þ
Si dice integrale generale del problema di Cauchy corrispondente una famiglia di soluzioni y(t,c1,....,cn) definita al variare di (t,c1,....,cn) Î I x J1 x .... x Jn tale che :
a) " fissato (c1,....,cn) Î J la funzione j(t) = y(t,c1,....,cn) è soluzione del problema di Cauchy
b) " fissato (t0 , y0 , ... , y0(n-1) ) Î I xÂn esiste (c1,....,cn) Î J unica tale che y(t,c1,....,cn) soddisfa le condizioni iniziali
56) Integrale generale di un sistema lineare di equazioni differenziali :
Si consideri y´(t) = f(t, y(t)) ove f : I x Ân ® Ân è continua e globalmente lipschitziana Þ
Si dice integrale generale di y´(t) = f(t, y(t)) un vettore y(t,c) : (t,c) Î IxJ , J ÌÂn tale che :
a) " fissato c Î J la funzione j(t) = y(t,c) è soluzione
b) " fissato (t0 , y0) Î I xÂn esiste c Î J unico tale che j(t) = y(t,c) soddisfa la y(t0) = y0 .
57) Sistema lineare :
Si tratta di una equazione vettoriale del tipo ![]() con A(t) detta matrice dei coefficienti e b(t) detto termine noto.
con A(t) detta matrice dei coefficienti e b(t) detto termine noto.
Quadriche
58) Scrivere l´equazione generica della ellissoide e descriverne le varianti:
![]()
si chiama ellissoide perché se lo tagliamo lungo la asse z = 0 , x = 0 , y = 0 le sezioni sono ellissi.
le varianti sono :
a) se al secondo membro c´è -1 allora l´ellissoide è immaginario
b) se il termine noto è 0 l´ellissoide si riduce ad un punto
59) Scrivere l´equazione generica della iperboloide ad una falda e descriverne le varianti:
![]()
si chiama iperboloide ad una falda perché se lo tagliamo lungo la asse y = 0 ed x = 0 le sezioni sono iperboli mentre se lo tagliamo lungo piani paralleli al piano xy otteniamo delle ellissi. Non ha varianti.
60) Scrivere l´equazione generica della iperboloide a due falde e descriverne le varianti:
![]()
si chiama iperboloide a due falde perché se lo tagliamo lungo la asse y = 0 ed x = 0 le sezioni sono iperboli mentre se lo tagliamo lungo piani paralleli al piano xy otteniamo delle ellissi solo per valori superiori di |c|
non ha varianti.
61) Scrivere l´equazione generica del cono e descriverne le varianti:
![]()
È una equazione omogenea in quanto compaiono tutti elementi dello stesso grado questo vuol dire che può essere costruito utilizzando soltanto un fascio di rette. Da un punto di vista matematico coincide con la norma.
le varianti sono.
a) se il coefficiente di z2 è positivo allora il cono è immaginario.
62) Scrivere le equazioni dei paraboloidi e descriverne le caratteristiche:
![]() è un paraboloide ellittico, è evidente che le sue sezioni sono delle ellissi , non è che una coppa convessa, per valori di z minori di 0 viene descritto un paraboloide ellittico immaginario.
è un paraboloide ellittico, è evidente che le sue sezioni sono delle ellissi , non è che una coppa convessa, per valori di z minori di 0 viene descritto un paraboloide ellittico immaginario.
![]() è un paraboloide iperbolico o sella, è evidente che le sue sezioni lungo piani paralleli al piano xy sono delle iperboli mentre sezioni parallele al piano yz sono delle parabole concave mentre le sezioni parallele al piano zx sono delle parabole convesse.
è un paraboloide iperbolico o sella, è evidente che le sue sezioni lungo piani paralleli al piano xy sono delle iperboli mentre sezioni parallele al piano yz sono delle parabole concave mentre le sezioni parallele al piano zx sono delle parabole convesse.
63) Scrivere le equazioni dei cilindri e descriverne le caratteristiche:
![]() è un cilindro ellittico
è un cilindro ellittico
![]() è un cilindro ellittico immaginario
è un cilindro ellittico immaginario
![]() è un cilindro iperbolico
è un cilindro iperbolico
![]() è un cilindro parabolico
è un cilindro parabolico
64) Per quali riduzioni di quadriche si ottengono dei piani?
a) 2 autovalori e corrispondenti termini lineari nulli
x2 = tn Þ se tn > 0 si hanno 2 piani reali paralleli
se tn = 0 si hanno 2 piani reali coincidenti
se tn < 0 si hanno 2 piani complessi paralleli
b) 1 autovalore 0 ed altri 2 di segno discorde, tn = 0
x2 - y2 = 0 Þ 2 piani incidenti
c) 1 autovalore 0 e gli altri 2 di segno concorde, tn = 0
x2 + y2 = 0 Þ 2 piani complessi incidenti la cui intersezione è la asse reale z.
Integrazione multipla
65) Intervallo pluridimensionale :
È la produttoria I1* I2* I3* ... * In essendo Ii un intervallo limitato di estremi ai e bi .
La sua misura è ![]()
66) Plurintervallo :
Si tratta della unione P = ![]() essendo Qi un intervallo che non ha altri punti in comune con altri intervalli.
essendo Qi un intervallo che non ha altri punti in comune con altri intervalli.
La misura del plurintervallo è pari alla somma delle misure degli intervalli Qi che lo costituiscono.
67) Misura interna di un insieme limitato A mi(a) :
Si tratta della estremo superiore della misura dei plurintervalli contenuti in A.
68) Misura esterna di un insieme limitato A m e(a) :
Si tratta della estremo inferiore della misura dei plurintervalli che contengono A.
69) Insieme misurabile :
Un insieme è detto misurabile se sono uguali la misura interna e la misura esterna.
70) Decomposizione regolare :
Una famiglia di insiemi ![]() è detta decomposizione regolare della insieme T se :
è detta decomposizione regolare della insieme T se :
a) ogni insieme Ti è limitato e misurabile
b) l´unione degli insiemi Ti restituisce l´insieme T
71) Ampiezza di una decomposizione regolare ![]() :
:
Si tratta del massimo dei diametri dei Ti .
72) Dominio :
È l´insieme dato dalla unione di un insieme con la sua frontiera.
73) Cilindroide :
È il solido individuato dai punti x, y, z tali che x ed y appartengono al dominio TÌ Â2 mentre la z varia tra 0 ed f(x,y).
74) Funzione integrabile secondo Cauchy :
Una funzione limitata si dice integrabile secondo Cauchy su di un compatto misurabile T se esiste finito ![]() essendo : d è la ampiezza della decomposizione regolare
essendo : d è la ampiezza della decomposizione regolare
A è una decomposizione regolare di T
p è l´insieme dei punti mi ciascuno dei quali appartiene ad un diverso Ti .
sA,p è la misura di Cauchy pari alla somma ![]()
Il limite è finito se " e >0 esiste un d0 >0 tale che per ogni decomposizione regolare A di ampiezza d(A) < d0 e per ogni insieme p di punti si ha che | sA,p - l | < e .
75) Dominio semplice rispetto alla asse x :
È un dominio tale che a < x < b mentre a(x) < y < b(x)
76) Dominio semplice rispetto alla asse y :
È un dominio tale che c < y < d mentre a(y) < x < b(y)
77) Dominio semplice rispetto al piano xy :
È un insieme costituito da punti (x,y,z) tali che x ed y appartengono al dominio mentre a(x,y) < z < b(x,y)
Funzioni implicite
78) Equazione della retta tangente al grafico della funzione implicita nel punto x0 , y0 :
![]()
79) Insieme di livello :
È l´insieme che si ottiene proiettando sul piano z = 0 l´insieme ottenuto intersecando il grafico di z = g(x,y) con il piano z = c
80) Punto singolare o critico :
Si tratta di un punto in cui il gradiente della funzione Ñg(x0 , y0) = 0 è detto singolare im quanto non è applicabile il teorema di Dini.
81) Caratteristica della insieme di livello :
Se l´insieme di livello è privo di punti singolari, in ogni suo punto la tangente è ortogonale alla direzione di massima crescita di g in quel punto ossia Ñg .
82) Inviluppo di una famiglia di curve :
Si tratta di una curva tangente, in ogni suo punto non singolare, ad una ed una sola curva della famiglia.
Estremi vincolati
83) Jacobiano :
È il determinante della matrice  essendo j e y superfici di Â3 che individuano una curva. Esso rappresenta il tasso di variazione relativa della area, subordinata al cambio di variabili.
essendo j e y superfici di Â3 che individuano una curva. Esso rappresenta il tasso di variazione relativa della area, subordinata al cambio di variabili.
84) Punto regolare :
Si tratta di un punto nel quale la g(x,y) = 0 definisce implicitamente una funzione vincolo affinche ciò avvenga, per il teorema di Dini deve essere Ñg(x0 , y0) ¹ 0 . Per De Blasi invece un punto è regolare se il rango del Jacobiano è 2.
85) Punto critico o stazionario vincolato :
Si tratta di un punto regolare per il vincolo nel quale si annulla la derivata della funzione obiettivo in direzione tangente al vincolo. Per De Blasi invece un punto è regolare se il rango del Jacobiano è £ 1.
86) Lagrangiana :
È l´equazione f(x,y) - l g(x,y)
Analisi vettoriale
87) Parametrizzazione di un sottoinsieme di Â3 :
Si tratta di una funzione continua r : I®Â3 la cui immagine è il sottoinsieme di Â3 anche detto sostegno della curva e coincidente con la traiettoria.
88) Parametrizzazione semplice :
Una parametrizzazione è semplice se la funzione r è iniettiva.
89) Curva :
Coincide con la coppia (sostegno , parametrizzazione).
90) Curva piana :
è una curva il cui sostegno è contenuto in un piano.
91) Orientazione di una curva :
L´orientazione è funzione della parametrizzazione, la quale ha come dominio  che è orientato e pertanto lo sarà anche a curva.
92) Curva regolare :
È una curva avente parametrizzazione derivabile e r´(t) ¹ 0 per ogni t Î I.
93) Curve equivalenti :
Due curve sono dette equivalenti se possono essere ottenute una dalla altra con un cambio di parametro che non muti l´orientazione.
94) Curve omotope :
Due curve g1 e g2 sono dette omotope in E se esiste una funzione continua j = j(t,l) , (t,l) Î [a,b]x[0,1] tale che :
a) j(t,0) = r1(t) ; j(t,1) = r2(t) " t Î[a,b]
b) j(a,l) = pa ; j(b,l) = p(b) " t Î[0,1]
ed infine " l Î[0,1] , la curva gl di equazione j = j(t,l) sia contenuta in E.
95) Lunghezza di una curva :
![]()
Si ottiene applicando il teorema di Pitagora all´incremento infinitesimo per calcolare ds e poi sommando i ds.
96) Ascissa curvilinea :
È la distanza percorsa calcolata lungo la traiettoria a partire da un punto iniziale, essa vale :
![]()
derivando si ottiene che s´(t) > 0 in quanto la norma è positiva e pertanto la parametrizzazione mediante ascissa curvilinea è positivamente equivalente.
97) Integrale curvilineo di 1ª specie :
Ad ogni elemento infinitesimo della curva è assegnata una proprietà scalare, l´integrale curvilineo di 1ª specie non fa altro che calcolare la somma di questi contributi lungo tutta la curva, in formule :
![]()
nel caso che f = 1 l´integrale restituisce la lunghezza della curva, pertanto questo integrale è indipendente dall´orientazione della curva stessa.
98) Esempi di utilizzo della integrale curvilineo di 1ª specie :
a) calcolo della massa di un filo ![]()
b) calcolo del baricentro del filo stesso 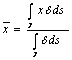
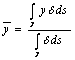
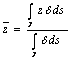
c) calcolo del momento d´inerzia di un filo rispetto ad un asse ![]()
99) Forma differenziale lineare o 1-forma :
È la forma lineare associata al campo vettoriale F1(x,y,z)i + F2(x,y,z)j + F3(x,y,z)k essa vale w = F1 dx + F2 dy + F3 dz
si può quindi pensare come il prodotto vettoriale tra la forza e lo spostamento infinitesimo e rappresenta quindi il lavoro compiuto dalla forza per spostare il suo punto di applicazione.
100) Integrale curvilineo di 2ª specie :
È il lavoro che il campo F compie per spostare il suo punto di applicazione da a in b.
![]()
Il suo valore è indipendente dalla parametrizzazione a patto che si tratti di parametrizzazioni equivalenti ossia che mantengono l´orientazione.
101) Forma differenziale lineare chiusa :
w è detta chiusa se rot F = 0 o in altre parole se il campo è conservativo. Per De Blasi invece si ha che
w = F1 dx + F2 dy + F3 dz è chiusa se Xy = Yx , Yz = Zy , Xz = Zx .
102) Insieme semplicemente connesso :
Un insieme E è semplicemente connesso se ogni curva chiusa in esso contenuta è frontiera di un insieme limitato interamente contenuto in E ossia se ogni curva chiusa può essere deformata sino a ridurla ad un punto rimanendo all´interno della insieme.
103) Forma differenziale lineare esatta :
w è detta esatta se esiste una funzione potenziale U che sia primitiva di w ossia F = ÑU da un punto di vista pratico si deve controllare che w sia chiusa ossia che rot F = 0 dopodiché se il dominio è semplicemente connesso, allora w è esatta mentre se non lo è allora w è esatta solo localmente.
104) Fattore integrante :
Si definisce fattore integrante di una forma differenziale lineare w non esatta una funzione m derivabile tale che m w è esatta, nel piano è sempre possibile individuare tale fattore integrante..
105) Come calcolare la funzione potenziale U :
Ci si deve prima accertare che w sia esatta dopodiché si applica la seguente formula :
![]()
106) Cammino camm(a,b) :
È l´insieme di tutti i percorsi che congiungono il punto a con il punto b.
107) Cammino poligonale cammp(a,b) :
È l´insieme di tutte le poligonali che congiungono il punto a con il punto b.
108) Campo vettoriale conservativo :
Un campo vettoriale è detto conservativo se esiste una funzione potenziale U il cui gradiente è F ossia ÑU = F .
109) Campo vettoriale irrotazionale :
Un campo vettoriale è detto irrotazionale se rot F = 0.
110) Campo radiale :
È un campo il cui valore dipende solo dalla distanza dall´origine, è un campo conservativo, ammette cioè potenziale.
111) Insieme stellato :
Un insieme E è detto stellato se esiste un suo punto p0 tale che il segmento di retta che lo congiunge con un qualsiasi altro punto della insieme è interamente contenuto in E.
112) Calcolo di aree mediante il teorema di Gauss Green :
![]()
113) Formula di Stokes nel piano :
È semplicemente una formulazione vettoriale della formula di Gauss Green, si ha : ![]()
essendo T il versore tangente alla curva delimitante D che si ottiene derivando la parametrizzazione.
114) Formula della divergenza nel piano :
Si ottiene anche questo dal teorema di Gauss Green ponendo P al posto di Q e -Q al posto di P ottenendo al primo membro l´integrale di superficie di una divergenza e al 2° membro la circuitazione del prodotto scalare tra il vettore F ed il versore normale uscente. In formule si ha : ![]()
115) Superficie :
Una superficie in Â3 è una coppia (S,r) essendo S un insieme di Â3 ed r una sua parametrizzazione.
116) Punto regolare di una superficie :
Un punto p = r( u0 , v0) si dice regolare se la matrice  ha rango 2 ossia è possibile individuare una rappresentazione cartesiana della superficie stessa.
ha rango 2 ossia è possibile individuare una rappresentazione cartesiana della superficie stessa.
117) Dominio piano di Jordan :
T è un dominio limitato delimitato da un circuito semplice orientato g detto bordo di T
118) Bordo positivo di un dominio di Jordan :
Bordo positivo è quello che vede la coppia ordinata (t,n) costituita dal vettore tangente e dal vettore normale orientata concordemente alla coppia ordinata dei versori i , j del piano. Un´altra definizione è che la superficie deve sempre essere percorsa con il vettore normale verso l´insieme.
119) Superficie chiusa :
È una superficie senza bordo e limitata in Â3 .
120) Superficie regolare a pezzi :
È una superficie regolare per la quale esistono un numero finito di curve regolari a tratti g1 , ... , gn contenute in S che la suddividono in un numero finito di superfici regolari dette facce.
121) Linee coordinate di una superficie :
u è la curva che si ottiene dalla parametrizzazione r(u, v) dove v è costante. Il vettore tangente è ru(u,v) .
v è la curva che si ottiene dalla parametrizzazione r(u, v) dove u è costante. Il vettore tangente è ru(u,v) .
Con questa rappresentazione si può stabilire se la superficie è regolare verificando che sia ru ^rv = 0 .
122) Parametrizzazioni equivalenti :
Sono 2 parametrizzazioni legate da un cambiamento di parametro con determinante jacobiano positivo.
123) Equazione del piano tangente ad una superficie in un punto. :
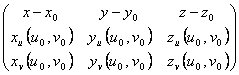 = 0
= 0
124) Vettore normale ad una superficie :
È il vettore dato dal prodotto vettoriale ru ^ rv .
125) Versore normale ad una superficie cartesiana :
Si ricava da rx ^ ry dividendolo per la sua norma si ottiene : 
126) Verso del versore normale uscente nelle parametrizzazioni di superfici cartesiane :
Il versore normale esterno è diretto verso la alto.
127) Superficie orientabile :
Una superficie è detta orientabile se è regolare e preso un qualsiasi circuito chiuso ed un punto P su di esso , il vettore normale percorre con continuità il circuito chiuso e si ripresenta nel punto P con lo stesso orientamento. I casi più drammatici di superfici non orientabili sono il nastro di Mobius e l´otre di Klein.
128) Area di una superficie :
![]()
129) Integrale di superficie di una funzione h(x,y,z) :
![]()
130) Coordinate del baricentro di una distribuzione di massa superficiale :
![]()
![]()
![]()
131) Centroide :
Si tratta del baricentro nel caso particolare in cui la distribuzione di massa sia costante.
132) Momento d´inerzia di una distribuzione di massa superficiale : ![]()
133) 2_Forma :
È una forma del tipo w = X dy^dz + Y dz^dx + Z dx^dy
134) Flusso di un vettore attraverso una superficie S :
![]()
135) Dominio semplicemente decomponibile :
T Ì Â3 è un dominio di Jordan semplicemente decomponibile se T è connesso e risulta essere unione disgiunta di un numero finito di domini di Jordan semplici.
136) Campo solenoidale :
Un campo vettoriale F è detto solenoidale se la sua divergenza è nulla div F = 0.
137) Insieme superficialmente connesso o fortemente connesso :
Un insieme è detto superficialmente connesso se ogni superficie chiusa regolare a tratti contenuta in T delimita un dominio limitato contenuto tutto in T.
138) Formula per il calcolo di un potenziale vettore :
F = F2j + F3k dove ![]() e
e ![]()
139) Come utilizzare il teorema della divergenza per il calcolo dei volumi :
Occorre considerare il campo vettoriale F = x i + y j + z k non il campo F = i + j + k il quale restituisce sempre un volume 0.
140) Angolo solido :
Sia dS un elemento di superficie e congiungiamo tutti i punti del contorno di dS con l´origine O venendo in tal modo a formare un cono. Sia ora dW l´intersezione tra una sfera di centro O e raggio r ed il cono precedente Þ la angolo solido dw è individuato dal rapporto tra questa area ed il quadrato della distanza dall´origine ![]() essendo
essendo ![]() dunque la angolo solido è
dunque la angolo solido è ![]() .
.
