Spazi Vettoriali
1) Descrivere lo spazio vettoriale Rn :
È il prodotto cartesiano della insieme R dei ni reali per se stesso n volte ossia Rn = R * R * R * .... *R.
In particolare un vettore viene rappresentato con le sue coordinate riferite rispetto alla origine, tale origine può variare a seconda del valore di n.
Per n = 2 ci troviamo in R2 ossia il piano cartesiano O![]() .
.
Per n = 3 ci troviamo in R3 ossia nello spazio O![]() .
.
Per n = 4 non riusciamo ad immaginare che genere di spazio rappresenti, tuttavia O![]() .
.
2) Spazio vettoriale reale :
Uno spazio vettoriale si definisce reale se in esso sono definite le seguenti operazioni:
1) È in esso presente l´elemento 0 , si tratta di un vettore avente tutte le coordinate con coefficiente 0.
2) Addizione di vettori Þ Si effettua graficamente con la regola del parallelogramma e praticamente
![]() +
+ ![]() =
= ![]() =
= ![]() si tratta di un vettore del piano uscente dall´origine e culminante nel punto di coordinate ascissa = 3 , ordinata = 8.
si tratta di un vettore del piano uscente dall´origine e culminante nel punto di coordinate ascissa = 3 , ordinata = 8.
Per la somma sono inoltre definite le seguenti 4 proprietà o assiomi:
a) ASSOCIATIVA Þ " x, y, z Î V x + y + z = (x + y) + z = x + (y + z)
b) COMMUTATIVA Þ " x , y Î V x + y = y + x
c) ZERO Þ " x Î V x + 0 = x
d) VETTORE OPPOSTO Þ " x Î V $ x1 Î V : x + x1 = 0
3) La moltiplicazione tra vettori è una operazione che in Rn non ha senso, è invece utilizzata la moltiplicazione di un vettore per uno scalare, e si esegue moltipicando tutte le coordinate del vettore per quello scalare l.
5![]() =
= ![]() =
= ![]()
Per la moltiplicazione sono inoltre definite le seguenti 4 proprietà o assiomi:
a) ASSOCIATIVA Þ " x Î V, "l , m Î R x (lm) = (xl)m = (xm)l
b) DISTRIBUTIVA SOMMA SCALARI Þ " x Î V, "l , m Î R x (l+m) = xl + xm
c) DISTRIBUTIVA SOMMA VETTORI Þ " x , y Î V, "l Î R (x +y)l = xl + yl
d) UNITA´ Þ " x Î V x * 1 = x
R[x] = Polinomio con coefficienti complessi della variabile x è un tipico spazio Rn con n pari al grado del polinomio.
Tutto quanto abbiamo detto per Rn è applicabile anche a Cn con l´unica differenza che nelle definizioni si dovrà sostituire l , m Î Rn con l , m Î Cn essendo C , l´insieme dei ni complessi, pertanto le operazioni di somma e di prodotto andranno eseguite secondo quanto affermato per i ni complessi.
C[x] = Polinomio con coefficienti complessi della variabile x è un tipico spazio Cn con n pari al grado del polinomio stesso.
Abbiamo dimostrato che le proprietà degli assiomi sono verificate in Rn .
2) Prodotto scalare in Ân:
Avendo a disposizione 2 vettori, moltiplicare uno per la altro non ha alcun senso, ma ha invece senso eseguire il prodotto scalare dei 2 vettori, questo si ottiene eseguendo la somma dei prodotti ordinati dei singoli elementi dei vettori
v :=![]() , w :=
, w :=![]() < v,w > = (-1*4) + (1 *3) + (4 * 6) + (3*1) = 26
< v,w > = (-1*4) + (1 *3) + (4 * 6) + (3*1) = 26
Come si nota il prodotto scalare rappresenta un n° il cui significato si deduce dal seguente disegno:
![]()
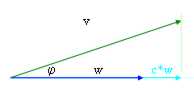 b = p/2
b = p/2
Ossia il prodotto scalare non è che il n° per il quale dobbiamo moltiplicare il vettore w affinche sia lungo quanto la proiezione ortogonale di v sulla sua direttrice.
Il prodotto scalare per essere tale deve avere le seguenti proprietà :
1) Commutativa < x , y > = < y , x >
2) Distributiva < x , y + z > = < x , y > + < x , z >
3) Omogeneità l * < x , y > = < lx , y > = < x , ly >
4) Positività < x , x > > = 0
In particolare quindi il prodotto scalare è in grado di dirci se 2 vettori sono ortogonali, infatti in tal caso la proiezione sarà nulla e così pure il prodotto scalare.
3) Norma:
La norma è intimamente legata al concetto di prodotto vettoriale, rappresenta anche essa un n° scalare che questa volta non è legato alla proiezione di un vettore su di un altro bensì alla lunghezza di un vettore, secondo quanto detto è facile assoggettarla al Teorema di Pitagora dal quale trae numerose proprietà ma del quale è diretta conseguenza solamente nel caso in cui venga considerato un angolo di p / 2 tra 2 vettori.
La norma viene sempre riferita ad un unico vettore.
|| x || = ![]() =
= 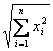
ossia essa equivale alla radice del prodotto scalare del vettore per se stesso e quindi alla radice della somma dei quadrati dei singoli elementi del vettore. La norma deve possedere le 3 seguenti proprietà immediatamente discendenti anche esse dal prodotto scalare:
1) || x || > = 0
2) || l * x|| = | l| * || x ||
3) || x + y || < = || x || + || y || ; questo è direttamente il teorema di pitagora in cui l´ipotenusa è sicuramente minore degli altri 2 lati altrimenti il triangolo non si chiuderebbe.
La terza proprietà è figlia della disuguaglianza di Cauchy - Schwarz che dice:
| < x , y > | < = || x || * || y ||
4) Sottospazi Vettoriali:
Scelto un sottoinsieme dello spazio vettoriale V , esso può essere o meno un sottospazio vettoriale, lo è nel caso siano ancora verificate le proprietà che distinguono uno spazio vettoriale ossia :
1) Presenza dello 0.
2) Somma tra vettori.
3) Moltiplicazione di un vettore per uno scalare.
In generale però esiste anche un sistema più breve per verificare se un sottoinsieme di uno spazio vettoriale sia un sottospazio vettoriale, deve essere cioè soddisfatta la seguente:
W Î V è un sottospazio vettoriale se " w1 , w2 Î W e " l , m Î R
anche lw1 + mw2 Î W
Questo sistema è completamente equivalente al primo in quanto ad esso riconducibile, infatti:
caso 1) Si può porre l = m = 0
caso 2) Si può porre l = m = 0
caso 3) Si può porre w1 o m = 0
In particolare :
Il sottoinsieme ![]() è il più piccolo sottoinsieme ed appartiene ad ogni spazio vettoriale.
è il più piccolo sottoinsieme ed appartiene ad ogni spazio vettoriale.
Il sottoinsieme V è il più grande sottoinsieme ed appartiene ad ogni spazio vettoriale.
5) Costruzioni generali di sottospazi:
Iniziamo definendo una combinazione lineare come un vettore costituito dal prodotto di k vettori appartenenti a V spazio vettoriale con i coefficienti a1, ... , ak. Si presenta quindi nella forma:
3v1 + 5v2 + 2v3 +...+14vn
Effettuare lo Span di un vettore v Î V spazio vettoriale significa generare un sottospazio dello stesso, questo avviene semplicemente pensando ad esempio ai multipli di uno stesso vettore, ma più in generale, avendosi 2 vettori lo Span rappresenta tutte le possibili combinazioni lineari degli stessi ovvero la somma dei prodotti dei singoli vettori per il rispettivo coefficiente ax ognuno dei quali può assumere qualsiasi valore appartenente ad Â.
Da notare che affinchè lo span sia un sottospazio devono essere verificate le condizioni del criterio breve o del criterio lungo di individuazione di sottospazi, ossia:
Criterio lungo : 1) Presenza dello 0.
2) Somma tra vettori.
3) Moltiplicazione di un vettore per uno scalare.
Criterio breve : W Î V è un sottospavio vettoriale se " w1 , w2 Î W e " l , m Î R
anche lw1 + mW2 Î W
Un tipico esempio di spazio vettoriale è quello descritto da un sistema omogeneo, ossia avente tutti i termini noti = 0 ;
lo span di un simile spazio vettoriale si ricava semplicemente trovando le soluzioni del sistema tramite la riduzione di Gauss. Queste soluzioni possono quindi essere scritte come combinazione lineare di più vettori. Esempio:
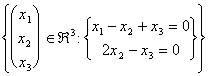
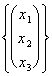
Ci chiede di determinare il sottospazio vettoriale in Â3 costituito da tutte le soluzioni possibili di questo sistema le quali possono generalmente esser scritte come Span di un n° di vettori variabili tra 1 ed n.
Come detto precedentemente per risolvere il sistema si applica Gauss alla matrice associata:
![]() si tratta di un sistema già a scala con una incognita libera avente soluzione nel vettore:
si tratta di un sistema già a scala con una incognita libera avente soluzione nel vettore:
![]()
 =
= 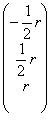 quest´ultimo vettore si può anche scrivere r *
quest´ultimo vettore si può anche scrivere r * ![]()
Quest´ultima forma ci dice che questo sottospazio di Â3 si può descrivere come Span 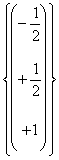
ossia è uno spazio vettoriale costituito da tutti multipli di questo vettore che si ottengono al variare di r ossia della incognita libera che è associata ad x3.
Esiste naturalmente anche il caso in cui lo Span è costituito da più di un vettore e questo avviene sempre quando la soluzione del sistema di equazioni prevede più di una incognita libera. In particolare il n° di vettori dello Span è uguale al n° delle incognite libere infatti ognuna andrà a moltiplicare un vettore ed in quel vettore ci dovranno essere i coefficienti di questa incognita libera associati alla rispettiva x mentre per le altre x i coefficienti nel vettore in questione dovranno essere tutti 0.
Ad esempio si supponga di trovare in un sistema le seguenti soluzioni:
![]()
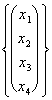 =
= 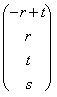 = r
= r![]() + s
+ s![]() + t
+ t![]()
e pertanto :
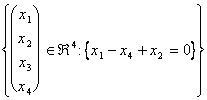 = Span
= Span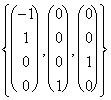
È da notare che lo Span è un generatore di spazi vettoriali che può essere dimensionato anche in eccesso, ossia è possibile aggiungere allo Span appena scritto anche un altro vettore che semmai è anche ricorsivo ma che non altera minimamente la definizione di Span che è stata enunciata.
6) Vettori linearmente indipendenti, dipendenti, concetto di base e di dimensione:
Partendo dall´esempio precedente e dalla limitazione che abbiamo detto è implicita nello Span, ci si domanda quanti vettori sono effettivamente necessari per descrivere uno spazio vettoriale ?
La risposta è simile al concetto di divisibilità dei n1 ossia abbiamo necessità dei ni primi che sappiamo essere indivisibili e generatori di tutti gli altri numeri. Analogamente, noi abbiamo bisogno di una base ossia di n vettori tramite i quali costruire tutti gli altri vettori del piano come combinazione lineare.
Si definisce pertanto base di uno spazio vettoriale un insieme ordinato di vettori v1,...,vt di V tali che :
1) Span { v1,...,vt } = V.
Cioè lo Span deve essere in grado di descrivere tutto V
2) I vettori v1,...,vt sono tra loro indipendenti.
Ossia non ci debbono essere relazioni tra 2 o più vettori dello Span, ad esempio non può essere uno multiplo della altro. In particolare nella combinazione lineare dovranno essere 0 tutti i coefficienti l , solo così infatti siamo certi che non c´è alcuna relazione tra i vettori presi in considerazione.
Se anche uno solo dei coefficienti l è diverso da 0 allora nello Span ci sono dei vettori ridondanti pertanto i vettori non sono tutti linearmente indipendenti e quindi si definiscono linearmente dipendenti.
Si definisce inoltre Dimensione di uno spazio vettoriale V, dim(V) il n° di vettori di cui è costituita la base.
È proprio questa appena enunciata la caratteristica che differenzia gli spazi vettoriali rispetto alla base, infatti ogni spazio vettoriale ha una base però possono presentarsi i 2 seguenti casi:
1) Spazio vettoriale molto grande Þ È il caso dei polinomi Â[X] = a+bx1+cx2+....+ txn , in essi la base esiste ma ha dimensioni infinite.
2) Spazio con dimensione finita Þ Ha un n° infinito di basi, ossia tutti i vettori che sono tra di loro indipendenti, tuttavia noi sappiamo che la dimensione di queste basi deve essere eguale per tutte.
Dimostrazione: si procede per assurdo dimostrando che 2 basi con dimensione diversa appartengono allo stesso spazio vettoriale, per farlo scrivo i vettori della base grande come combinazione lineare dei vettori della base piccola.
A questo punto per dimostrare che i vettori così creati non sono indipendenti, raccolgo tutti i coefficienti in una matrice e mi rendo conto che il n° di equazioni è inferiore del n° di incognite, pertanto vi saranno delle incognite libere che indubbiamente corrispondono ad una dipendenza dei vettori in questione tra di loro, pertanto non si trattava di una base diversa ma della stessa base.
Abbiamo già visto come ricavare uno Span, vediamo ora come accertarci che i vettori dello Span siano linearmente indipendenti. Ad esempio abbiamo i seguenti vettori Î Â4 :
![]() ,
, ![]() ,
, ![]() ,
, ![]()
che possono essere scritti come una combinazione lineare:
l1![]() + l2
+ l2![]() + l3
+ l3 ![]() + l4
+ l4![]()
che danno vita alla matrice associata:
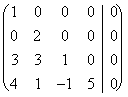 la quale dà come soluzione
la quale dà come soluzione ![]()
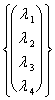 =
= ![]()
Pertanto i vettori sono linearmente indipendenti e potrebbero dar luogo ad una base dello spazio considerato.
se invece la matrice fosse stata la seguente:
 che ridotta diviene
che ridotta diviene 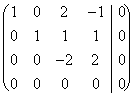
ossia una matrice con una equazione che si annulla e che quindi dà vita ad una incognita libera la quale rende i vettori dello Span descritto linearmente dipendenti questo occorre però sempre dimostrarlo ottenendo un caso in cui la combinazione lineare è 0 ma non sono 0 tutti i coefficienti l. Quindi :
 = r
= r![]() e quindi ponendo r = 1 : - 1
e quindi ponendo r = 1 : - 1![]() - 2
- 2![]() + 1
+ 1![]() + 1
+ 1![]() =
= ![]()
Abbiamo dimostrato che una soluzione dove i l non sono tutti = 0 soddisfa ugualmente il sistema quindi questi vettori sono linearmente dipendenti e non rappresentano pertanto una base.
Si noti il seguente significato geometrico:
Linearmente indipendenti
* 2 vettori in Â2 sono indipendenti se hanno direzioni diverse
* 3 vettori in Â3 sono indipendenti se hanno direzioni distinte
Linearmente dipendenti
* 2 vettori in Â2 sono dipendenti se hanno la stessa direzione
* 3 vettori in Â3 sono dipendenti se hanno la stessa direzione oppure si trovano sullo stesso piano.
* 4 vettori in Â3 non possono che essere linearmente dipendenti
7) Affermazioni sulle quali si basa la ricerca di una base:
a) E' un insieme Massimale ossia costituito da vettori tra di loro indipendenti che divengono dipendenti se gliene viene aggiunto 1.
b) Una base è un tipico caso di insieme massimale
Dim : prendiamo una base B di V, gli aggiungiamo un vettore di V e ci accorgiamo che i vettori così ottenuti sono linearmente dipendenti in quanto se scriviamo questo vettore v come combinazione lineare degli altri e poi dal 1° membro lo portiamo al 2° ci rendiamo conto che esso ha coefficiente 1 mentre gli altri vettori hanno tutti coefficiente 0.
c) Se V = Span (A) e B Ì A è un insieme massimale allora è anche V = Span (B)
d) Ogni spazio vettoriale che contiene un sistema finito di generatori ammette una base
Dim: Þ sia V = Span(A) :
d1) V = { 0 } allora V non ha base
d2) confrontiamo v1 con tutti gli altri vettori, se sono tutti confronti dipendenti allora la base è v1 altrimenti prendiamo i confronti che hanno dato come risultato dei vettori indipendenti , avremo 2 vettori ad esempio v1 e v3 che sono indipendenti e candidati ad essere una base, allora li confrontiamo con tutti gli altri vettori con i quali v1 si era rivelato indipendente, e se anche questi 3 vettori sono indipendenti allora continuiamo a confrontare con gli altri vettori che confrontati con v1 avevano dato esito indipendenti. Giungiamo alla base quando troviamo dei vettori dipendenti, la base sono tutti i vettori meno l´ultimo considerato. Se i vettori sono in n° esorbitante, la base esiste ma i confronti sono in n° esorbitante anche essi e la base, ipoteticamente infinita.
8) Completamento della base:
Sia B una base di V costituita da n vettori ed in V siano presenti m vettori indipendenti allora possiamo dire questi m vettori di V insieme a n - m vettori di B formano una base di V.
Dim: Þ La dimostrazione è secondo il principio di induzione, avviene cioè prima per 1 vettore e poi la estendiamo a tutti i vettori:

a) Supponiamo di avere in V il solo w1 linearmente indipendente rispetto a se stesso. Lo scriviamo come combinazione lineare dei vettori della base, w1 = l1v1 + l2 v2 + l3v3 +... , +lnvn notiamo che affinchè w2 sia indipendente deve essere m1 ¹ 0 in quanto tutti i l sono uguali a 0 essendo una base. ma se w1 ¹ 0 allora anche uno dei l deve essere diverso da 0 per poter verificare l´uguaglianza, supponiamo che sia v1 e riscriviamo l´equazione in funzione di v1 dividendo per l1 il secondo membro. All´equazione così ottenuta sostituiamo a w1 la sua combinazione lineare ed otteniamo che affinchè sia vera avendo posto l1 ¹ 0 , dovrà essere 0 il coefficiente per cui è moltiplicato, cioè il coefficiente di w1 pertanto i vettori m1w1 + m2 v2 + m3v3 +... , +mnvn sono una base di V in quanto B Ì Span(w1 , v2 , v3, vn).
b) Ragionamento analogo si compie per dimostrare che ciò vale anche per m vettori indipendenti di V che non fanno parte della base. La conclusione è che il n° di vettori della base e quindi la dimensione di V non rimane inalterata , è per questo che parliamo di completamento della base.
Da questa dimostrazione traiamo numerose osservazioni:
A) Le basi di uno spazio vettoriale hanno tutte la stessa dimensione, perchè se una avesse meno vettori, gliene potremmo aggiungere da un´altra, ma essendo la base massimale per definizione, ciò sarebbe un assurdo, l´unica situazione che rispetta la massimalità della base è la parità del n° di vettori tra basi.
B) Avendo uno spazio vettoriale con dimensione n, i suoi sottospazi non possono avere dimensione m > n.
Vediamo ora come effettuare il completamento ad una base:
Facciamo il caso di avere i 2 seguenti vettori v1 =![]() e v2 =
e v2 =![]() e di volerli completare ad una base di Â3 , possiamo scegliere uno dei vettori della base canonica, ma quale ci garantisce che i vettori sono ancora tra di loro indipendenti:
e di volerli completare ad una base di Â3 , possiamo scegliere uno dei vettori della base canonica, ma quale ci garantisce che i vettori sono ancora tra di loro indipendenti:
Gauss per colonne, ossia per vettori ci schiarisce un pò le idee, vediamo lo Span attuale di v1 e v2 e cerchiamo di fare qualche osservazione: ![]()
![]() Si tratta di un sistema in forma a scala, quindi questi 2 vettori sono indipendenti, è ben chiaro che l´unico vettore della base che consente di mantenere inalterata questa struttura a scala sia il vettore e3 così come segue:
Si tratta di un sistema in forma a scala, quindi questi 2 vettori sono indipendenti, è ben chiaro che l´unico vettore della base che consente di mantenere inalterata questa struttura a scala sia il vettore e3 così come segue: ![]()
![]()
![]() e dunque questa è una base di Â3 costituita quindi da 3 vettori indipendenti, il cui Span è tutto Â3 .
e dunque questa è una base di Â3 costituita quindi da 3 vettori indipendenti, il cui Span è tutto Â3 .
9) Spazi vettoriali: somma , intersezione, complemento:
Abbiamo analizzato quali operazioni insiemistiche si possono eseguire avendo 2 sottospazi, W1 e W2 dello spazio vettoriale V.
W1 Ç W2 Ì V Þ l´intersezione di 2 sottospazi vettoriali è ancora un sottospazio vettoriale di V.
Un caso particolare di intersezione è quella tra un insieme ed il suo complemento, tale intersezione deve essere {0}.
Facciamo ora un esempio su come calcolare l´intersezione tra 2 spazi vettoriali, a tal fine si supponga di avere i 2 seguenti Span di Â4 V =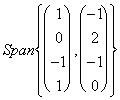 e W =
e W =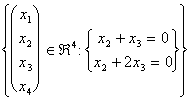 .
.
L´ intersezione che ci interessa, la possiamo individuare direttamente impostando che i vettori di W , oltre a rispondere alle specifiche fornite dalle 2 equazioni, siano anche contenuti nello Span di V.
Riassumiamo pertanto il vettore dei coefficienti l e m per V, si tratta del vettore delle soluzioni:
se ora sostituiamo x2 ed x3 nella definizione dei vettori di W troviamo esattamente l´intersezione tra i 2 sottospazi.  da cui ricaviamo l = m = 0 e pertanto
da cui ricaviamo l = m = 0 e pertanto  .
.
Ciò vuol dire esattamente che tra i due sottospazi non vi è alcuna intersezione pertanto la dim( V Ç W) = {0}..
W1 È W2 Þ non è sempre un sottospazio vettoriale di V, si pensi al caso di W1= Span del vettore del piano ![]() e W2 = Span del vettore
e W2 = Span del vettore![]() , essi rappresentano fasci di rette tra loro ortogonali, allora se noi prendiamo 2 vettori e ne facciamo la somma con il metodo del parallelogramma, tale somma risulterà essere un vettore con direzione diversa rispetto a tutti gli altri, pertanto la somma non è contenuta in V e quindi l´unione di 2 sottospazi di V non necessariamente è un sottospazio anche esso.
, essi rappresentano fasci di rette tra loro ortogonali, allora se noi prendiamo 2 vettori e ne facciamo la somma con il metodo del parallelogramma, tale somma risulterà essere un vettore con direzione diversa rispetto a tutti gli altri, pertanto la somma non è contenuta in V e quindi l´unione di 2 sottospazi di V non necessariamente è un sottospazio anche esso.
W1 + W2 Ì V Þ La somma in generale sostituisce l´unione ed è sempre un sottospazio vettoriale.
Un caso particolare di somma è quella costituita da 2 insiemi di cui uno è il complementare della altro, unicamente con questa condizione possiamo affermare che la somma si scrive in un unico modo, tale somma viene allora definita diretta.
Nel caso che l´intersezione dei 2 insiemi sia diversa da { o } allora ci sono più modi di scrivere la somma come nel caso seguente: si abbia in Â3 il seguente vettore , esso può essere scritto ![]() =.
=. ![]() +
+![]() =
= ![]() +
+![]()
Facciamo ora un esempio su come calcolare le dimensioni della somma di 2 spazi vettoriali, poniamo siano i seguenti Span di Â4 V =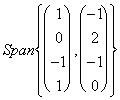 e W =
e W =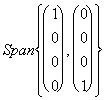 .uno dei metodi per calcolarne la somma è di unirli in una unica matrice e vedere se sono vettori indipendenti, così come segue:
.uno dei metodi per calcolarne la somma è di unirli in una unica matrice e vedere se sono vettori indipendenti, così come segue:
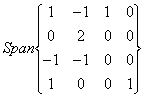 Tale controllo in tal caso va fatto per colonne, trattandosi di vettori e non di equazioni.
Tale controllo in tal caso va fatto per colonne, trattandosi di vettori e non di equazioni.
Tuttavia vi è anche un modo più rapido a seconda del problema, ossia attuare la formula di Grassmann, è chiaro che debbono essere conosciuti sia la dimensione di V , di W ed anche della loro intersezioneed applicate alla seguente:
Dati 2 sottospazi vettoriali U e W di V, è valida la seguente relazione : Dim(U) + Dim(W) =Dim(U + W) + Dim(U ÇW)
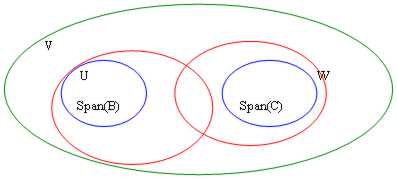
Abbiamo 2 generatori , B e C di 2 sottospazi U e W, possiamo dire allora che B È C è un insieme di generatori di UÈW. Tuttavia stiamo parlando unicamente di Span e non di basi, infatti l´unione di 2 basi potrebbe anche individuare dei vettori che non sono indipendenti
10) Insieme complementare:
Si definisce insieme complementare di A, l´insieme B tale che non abbia alcuna intersezione con A e che il tutto formi lo spazio vettoriale B secondo il disegno successivo:
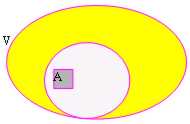
Facciamo a questo punto un esempio su come trovare un complemento di un determinato sottospazio vettoriale di uno spazio V.
Nell´esempio sul completamento della base , avevamo visto come completare i due vettori v1 =![]() e v2 =
e v2 =![]() ad una base di Â3, ed il risultato era la terna di vettori:
ad una base di Â3, ed il risultato era la terna di vettori: ![]()
![]()
![]() pertanto possiamo dire che un complemento di v1 avente dimensione 1 è il piano generato dai vettori
pertanto possiamo dire che un complemento di v1 avente dimensione 1 è il piano generato dai vettori ![]()
![]() . Analogamente il complemento in Â3 del piano generato dai vettori v1 e v2 è il vettore
. Analogamente il complemento in Â3 del piano generato dai vettori v1 e v2 è il vettore ![]() avente dimensione 1.
avente dimensione 1.
11) Teorema di Grassmann:
Dati 2 sottospazi vettoriali U e W di V, è valida la seguente relazione : Dim(U) + Dim(W) =Dim(U + W) + Dim(U ÇW)
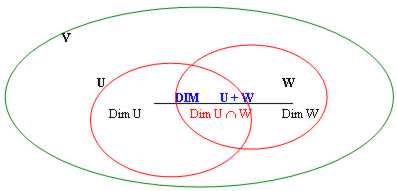
Che la dim della somma non sia tutto si intuisce anche visivamente pensando che nella somma vengono eliminati tutti i vettori che in qualche maniera sono ridondanti nelle singole dimensioni dei sottospazi. Quel qualcosa è rappresentato dalla intersezione.
Dimostrazione:
Abbiamo uv1 + uvn che è una base, la completiamo in U a uv1 + uvn + un+1 + up ed in W a uv1 + uvn + wn+1 + ws
Dobbiamo dimostrare che i vettori u che sono completamento dei vettori uw in U +
i vettori w che sono completamento dei vettori uw in W +
i vettori u che sono nella intersezione U Ç W =
devono essere una base di U + W ossia suo Span e tra loro indipendenti
affinchè ciò sia vero deve essere p+(n-p)+(s-p) = n + s - p = dim(U + W)
che equivale a dire: Dim(U) + Dim(W) =Dim(U + W) + Dim(U ÇW)
quindi B deve essere {uv1 + uvn + un+1 + up + wn+1 + ws} ed affinchè sia indipendente tutti i coefficienti (che non sono scritti) debbono essere = 0 . Lo dimostriamo osservando che " v Î (UÇW) , " u Î (U) ed " w Î (W), ma per essere w + v + u = 0 Þ w = -v -u Þ quindi w stà in (UÇW)e può quindi essere scritto come combinazione lineare di v, ma w è anche eguale a uv1 + uvn + wn+1 + ws che quindi devono essere anche essi indipendenti per verificare l´uguaglianza, quindi w quindi tutti i coefficienti di B sono 0.
Molto interessante per la mnemonica l´esempio fatto da Schoof. si supponga V un piano e W un piano ad esso ortogonale quindi entrambe con dimensione 2:
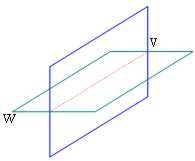
Come si può notare , l´intersezione tra i 2 piani è una retta avente dim = 1
pertanto dim(V+W) = dim(V) + dim (W) - dim(V Ç W) = 2 + 2 - 1 = 3
ed infatti 3 è esattamente la dimensione dello spazio.
12) Somma diretta:
Direttamente dal teorema di Grassmann discende la definizione di somma diretta infatti il teorema dice:
Dim(U) + Dim(W) =Dim(U + W) + Dim(U ÇW)
E da questo si nota bene che se l´intersezione tra 2 sottospazi vettoriali è nulla, allora la dimensione dello spazio somma è esattamente uguale alla somma delle dimensioni degli spazi addendi:

in formule Dim(A+B) = Dim(A) + Dim(B)
ed in questo caso quindi la somma si definisce diretta ed è possibile scriverla in un unico modo come già enunciato.
13) Applicazioni lineari:
Abbiamo analizzato il caso in cui ad uno spazio vettoriale venga applicata una funzione e l´immagine di questa funzione la abbiamo in un altro spazio vettoriale.
Abbiamo subito definito una applicazione come lineare se sono definite le seguenti:
Addizione f( v1 + v2) = f(v1) + f(v2)
Moltiplicazione f(lv) = lf(v)
Abbiamo quindi fatto l´esempio di una applicazione in V Î Â3 avente valori in W Î Â2 ossia
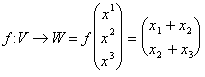 dobbiamo verificare se sia lineare ossia i 2 criteri:
dobbiamo verificare se sia lineare ossia i 2 criteri:
a) f( v1 + v2) = f(v1) + f(v2)
Il 1° membro vale: 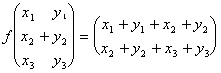
Il 2° membro vale: 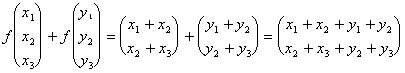
evidentemente i due membri sono uguali quindi si tratta di una applicazione lineare rispetto alla somma.
b) Moltiplicazione f(lv) = lf(v)
Il 1° membro vale: 
Il 2° membro vale: 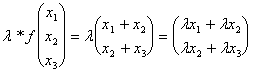
evidentemente i due membri sono uguali quindi si tratta di una applicazione lineare rispetto al prodotto.
Esiste poi anche un criterio breve per determinare se una applicazione è lineare che deriva direttamente dal criterio breve per la determinazione dei sottospazi, ossia:
criterio breve: ![]()
14) Immagine della funzione applicata ad uno spazio vettoriale:
L´immagine è definita come i vettori w Î W : esiste un vettore v in V : f(v) = w
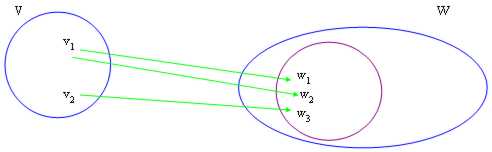
Abbiamo poi dimostrato che Im(f) è un sottospazio di W e che per definizione, se l´immagine di f è tutto W allora si dice che f è suriettiva, si ricordi che tutti i cowboy vengono colpiti da almeno una freccia.
Per il calcolo delle dimensioni della immagine si debbono trovare le soluzioni del sistema imposto dalla funzione e naturalmente essendo in n° illimitato, esprimerle come uno Span di alcuni vettori. Si supponga ad esempio di dover trovare le soluzioni della seguente: 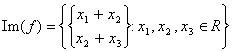
da cui 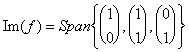 che equivale alla matrice Span
che equivale alla matrice Span![]()
che ridotta diviene: Span![]() nella quale si vede che un vettore era combinazione lineare degli altri 2, per cui possiamo dire che Im(f) =Span
nella quale si vede che un vettore era combinazione lineare degli altri 2, per cui possiamo dire che Im(f) =Span ed ha dimensione 2.
ed ha dimensione 2.
15) Nucleo di una applicazione lineare:
Si definisce invece nucleo di una applicazione lineare o Ker(f) tutti i vettori v in V che finiscono nello 0 della immagine
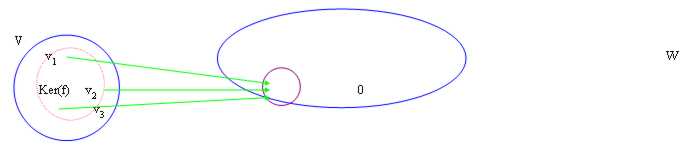
Abbiamo poi dimostrato che Ker(f) è un sottospazio di V.
16) Una funzione applicata ad uno spazio vettoriale è iniettiva se ker(f) = {0} ossia se non ci sono vettori nel nucleo:
La dimostrazione si suddivide in 2 parti:
a) Sapendo che f è iniettiva, cerchiamo di affermare che Ker(f) = {0}.ossia che il nucleo è vuoto.
Prendiamo un vettore v Î Ker(f) e diciamo che deve essere f(v) = 0 essendo la funzione iniettiva , possiamo però affermare che f(0) = 0 e quindi v = 0 cioè il vettore non esiste.
b) Sapendo che il nucleo è vuoto devo dimostrare che f è iniettiva ossia che ogni cowboy è colpito da una sola freccia.
Prendo 2 freccie, x ed y e dimostro che esse colpiscono 2 cowboys differenti f(x) ed f(y), se colpiscono lo stesso cowboy f(x) = f(y) allora era la stessa freccia x = y. Si dimostra sfruttando la linearità di f dicendo che deve essere f(x) - f(y) = 0 in quanto supponiamo f(x) = f(y) e vogliamo arrivare a dire che x = y.
Applicando la linearità deduciamo che 0 = f(x - y) ma il nucleo deve essere vuoto quindi x - y = 0 cioè x = y.
Vediamo a questo punto come si calcola il nucleo ker(f), risulta abbastanza intuitivo pensare che dobbiamo trovare tutte le soluzioni della funzione che valgono 0, pertanto ci riduciamo allo studio di un sistema omogeneo.
Si supponga di dover calcolare le dimensioni del nucleo della seguente applicazione f : Â3 in Â2.
 equivalente alla matrice
equivalente alla matrice ![]()
Si tratta di un sistema che normalmente deve essere risolto tramite Gauss per colonne ma in questo caso è già in forma a scala ed abbiamo 2 equazioni per 3 incognite, quindi una incognita è libera e già intuiamo che la dimensione sarà 1.
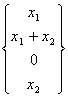
In particolare : ![]()
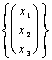 =
= ![]() quest´ultimo vettore si può anche scrivere r *
quest´ultimo vettore si può anche scrivere r * ![]() da cui implicitamente segue che : Ker (f) = Span
da cui implicitamente segue che : Ker (f) = Span![]() .
.
17) Matrice rappresentativa di una applicazione lineare:
La matrice rappresentativa compie una operazione che diversamente sembrerebbe alquanto complessa, essa riceve come ingresso una base dello spazio vettoriale contenente il dominio, una base dello spazio vettoriale contenente il codominio e la funzione che lega dominio e codominio, e fornisce come uscita un modo rapido per calcolare il valore della immagine per un qualunque vettore del dominio.
Normalmente come basi si scelgono quelle canoniche, tuttavia nessuno vieta di utilizzare basi qualsiasi purchè finite così come gli spazi da esse generati.
La spiegazione di come si ricavano e dialtri termini verrà fornita dinamicamente; vediamo come si ricava tale matrice per la seguente applicazione lineare:
g: Â3 ® Â2 : g = =
=![]() dobbiamo innanzitutto controllare che questa applicazione sia lineare ossia che siano rispettate le 2 seguenti uguaglianze:
dobbiamo innanzitutto controllare che questa applicazione sia lineare ossia che siano rispettate le 2 seguenti uguaglianze:
1) g( v1 + v2) = g(v1) + g(v2)
2) g(lv) = lg(v)
Scegliamo ora una base per Â3, naturalmente quella canonica e1 = ![]() , e2 =
, e2 = ![]() , e3 =
, e3 = ![]() .
.
Analogamente scegliamo ora una base per Â2, ancora quella canonica f1 =![]() , f2 =
, f2 =![]() .
.
A questo punto abbiamo tutto e possiamo quindi passare a descrivere la costruzione della matrice rappresentativa di g rispetto alle 2 basi utilizzate.
Le colonne della matrice rappresentativa sono infatti costituite dalla applicazione della funzione g ai vettori costituenti la base, cioè e1 , e2 , e3 . Nel nostro esempio, g(e1) =![]() , g(e2) =
, g(e2) =![]() , g(e3) =
, g(e3) =![]()
e la matrice rappresentativa è pertanto : ![]() .
.
dove il n° di colonne è pari alla dimensione del dominio ed il n° di righe è pari alla dimensione del codominio.
A questo punto siamo in grado di calcolare agevolmente cosa accade al vettore v1 = ![]() quando ad esso applichiamo la funzione g , semplicemente effettuando il prodotto tra la matrice rappesentativa e questo vettore:
quando ad esso applichiamo la funzione g , semplicemente effettuando il prodotto tra la matrice rappesentativa e questo vettore:
![]() *
*![]() =
= ![]() dove 5 è ottenuto moltiplicando la 1ª riga per la 1ª colonna mentre 7 è ottenuto moltiplicando la 2ª riga per la 1ª colonna secondo la normale moltiplicazione di un vettore per una matrice.
dove 5 è ottenuto moltiplicando la 1ª riga per la 1ª colonna mentre 7 è ottenuto moltiplicando la 2ª riga per la 1ª colonna secondo la normale moltiplicazione di un vettore per una matrice.
Naturalmente lo stesso risultato si poteva ottenere sostituendo direttamente il vettore v1 nella descrizione della funzione, tuttavia per grandi calcoli il procedimento migliore è questo appena illustrato.
Si noti che il vettore così ottenuto va inteso come un vettore di coordinate rispetto alla base fi fornita per il codominio.
È intuitivo ricavare che conoscendo unicamente la matrice rappresentativa si può ricavare la funzione semplicemente moltiplicando tale matrice per il vettore generico del dominio: ![]() *
*![]() =
= ![]() .
.
Si definisce rango di una matrice la dimensione della sua immagine, in questo caso il rango della matrice rappresentativa si trova, trovandone l´immagine ossia l´insieme delle soluzioni che come abbiamo visto si esprimono in termini di span ed i vettori che fanno parte dello span debbono essere tutti indipendenti, tuttavia non si può parlare di una base in quanto una funzione è una restrizione di un insieme e quindi lo Span non può essere tutto l´insieme così come invece dovrebbe essere per una base.
18) Matrici rappresentative di funzioni composte:
Il concetto di funzione composta è ben noto ed è riepilogato in figura:
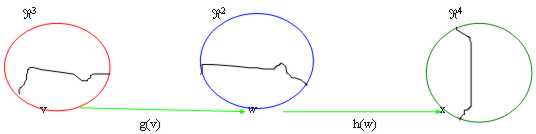
Si supponga :
g: Â3 ® Â2 : g = =
=![]() la cui matrice rappresentativa è :
la cui matrice rappresentativa è : ![]() .
.
h: Â2 ® Â4 : h =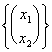 =
= la cui matrice rappresentativa è :
la cui matrice rappresentativa è : 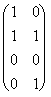 .
.
La matrice rappresentativa della funzione composta h ° g è il prodotto delle 2 matrici rappresentative:
h ° g =  *
*![]() =
=
Ad analogo risultato ma in amniera più ardua si giungeva sostituendo la funzione i due elementi generici della funzione
g = ![]() nella funzione h =
nella funzione h =  giungendo alla h ° g =
giungendo alla h ° g = 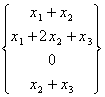
che applicata ai vettori della base di Â4 e1 = ![]() , e2 =
, e2 = ![]() , e3 =
, e3 = ![]() , e4 =
, e4 = ![]()
fornisce esattamente lo stesso risultato precedente ossia: h ° g = 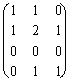 .
.
Nel comporre una matrice si deve stare attenti a comprendere se sia una operazione sensata o meno, in particolare deve
essere l´insieme di passaggio della stessa dimensione in arrivo rispetto alla dimensione in partenza, in pratica :
è possibile la composizione Â2 ® Â4® Â3
ma non è possibile la composizione Â2 ® (Â4 Â1)® Â3
Infatti una scrittura del tipo (Â4 Â1) non ha senso.
19) Applicazioni lineari biiettive:
Una funzione come sappiamo è biiettiva quando è sia iniettiva (ogni elemento della immagine può essere funzione di un unico elemento del dominio) che suriettiva (l´immagine è tutto il codominio).
la biiettività ci interessa fondamentalmente perchè essa la condizione affinchè una matrice rappresentativa della funzione g sia invertibile ossia esista l´inversa g-1.
La prima prerogativa di una matrice invertibile è che sia quadrata ossia che il n° di righe sia pari al n° di colonne.
Il procedimento per calcolarla è il seguente:
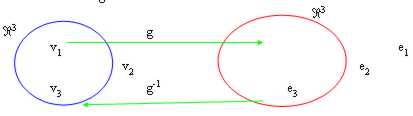
dalla illustrazione si comprende bene che il nostro scopo è individuare quegli elementi vi la cui immagine è la base del codominio ossia ei , ciò si ottiene risolvendo il sistema lineare g(vi) = ei.
Si supponga che la matrice rappresentativa sia :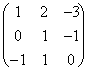 allora il sistema lineare è:
allora il sistema lineare è:
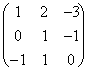 *
* ![]() = e1 =
= e1 = ![]() Þ
Þ ![]() =
= ![]() che è la 1ª colonna della matrice inversa.
che è la 1ª colonna della matrice inversa.
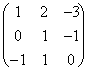 *
* ![]() = e2 =
= e2 = ![]() Þ
Þ ![]() =
= ![]() che è la 2ª colonna della matrice inversa.
che è la 2ª colonna della matrice inversa.
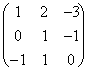 *
* ![]() = e3 =
= e3 = ![]() Þ
Þ ![]() =
= ![]() che è la 3ª colonna della matrice inversa.
che è la 3ª colonna della matrice inversa.
pertanto la matrice inversa della matrice rappresentativa 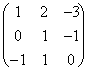 è la matrice
è la matrice 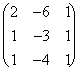 .
.
Si noti che si poteva giungere al medesimo risultato risolvendo la seguente matrice:
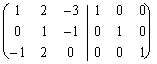 per ottenere a destra la matrice inversa debbo cercare di ridurre la matrice di sinistra ad una matrice diagonale così come al momento è a destra.
per ottenere a destra la matrice inversa debbo cercare di ridurre la matrice di sinistra ad una matrice diagonale così come al momento è a destra.
Cominciamo riducendo ad un sistema a scala: 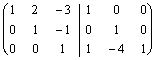 e poi partendo dal pivot in basso, creiamo 0 sopra tutti i pivot con il solito metodo di Gauss, otteniamo:
e poi partendo dal pivot in basso, creiamo 0 sopra tutti i pivot con il solito metodo di Gauss, otteniamo: 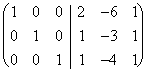 che , a destra presenta esattamente la matrice inversa che cercavamo ed è uguale a quella trovata col metodo lungo.
che , a destra presenta esattamente la matrice inversa che cercavamo ed è uguale a quella trovata col metodo lungo.
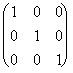
Posso inoltre controllare che il risultato ottenuto sia corretto, infatti se moltiplico la matrice rappresentativa per la corrispondente matrice inversa debbo ritrovare la base dalla quale sono partito per la definizione della matrice rappresentativa. Pertanto nel caso precedente: 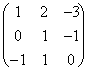 *
*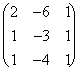 =
=
Dove il prodotto si esegue alle solite:
1ª riga per 1ª colonna
2ª riga per 1ª colonna
3ª riga per 1ª colonna
1ª riga per 2ª colonna
etc....
3ª riga per 3ª colonna.
20) Quando una matrice rappresentativa non è invertibile:
Non sapremo mai a priori se una matrice sia invertibile o meno, l´unico modo per rendercene conto è portare avanti i calcoli sin quando non si giunge ad un assurdo come il seguente: 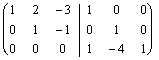 dove la 3ª equazione ci dice che 0 è uguale a 3 coefficienti diversi, il che è 3 volte assurdo in quanto 0 è uguale soltanto a 0.
dove la 3ª equazione ci dice che 0 è uguale a 3 coefficienti diversi, il che è 3 volte assurdo in quanto 0 è uguale soltanto a 0.
Un altro caso di assurdità di equazioni è il seguente: 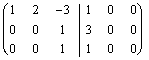 dove la 3ª incognita ci dice che x3 deve essere uguale ad 1 mentre la 2ª equazione ci dice che x3 deve essere uguale a 3, non possono essere vere entrambe contemporaeamente, quindi il sistema non ha soluzione e quella matrice rappresentativa non è pertanto invertibile.
dove la 3ª incognita ci dice che x3 deve essere uguale ad 1 mentre la 2ª equazione ci dice che x3 deve essere uguale a 3, non possono essere vere entrambe contemporaeamente, quindi il sistema non ha soluzione e quella matrice rappresentativa non è pertanto invertibile.
21) Cambiamento di base:
Si supponga ora di avere una matrice rappresentativa di Â3 impostata secondo la base canonica, e di volerla invece impostare secondo la seguente base: e11 = ![]() , e21 =
, e21 = ![]() , e31 =
, e31 = ![]() .
.
La matrice rappresentativa rispetto alla base canonica è la seguente:  dobbiamo ora calcolare la matrice rappresentativa rispetto alla nuova base, procediamo osservando che le colonne sono appunto la funzione applicata ai singloli vettori della base. Procediamo pertanto:
dobbiamo ora calcolare la matrice rappresentativa rispetto alla nuova base, procediamo osservando che le colonne sono appunto la funzione applicata ai singloli vettori della base. Procediamo pertanto:
f(e11) =  *
*![]() =
=![]() , f(e21) =
, f(e21) =  *
*![]() =
=![]() , f(e31) =
, f(e31) =  *
*![]() =
=![]()
Adesso debbo trovare quali coefficienti, moltiplicati per la base e1 mi danno come risultato questi 3 vettori, pertanto :
f(e11) =  avente come soluzioni:
avente come soluzioni: 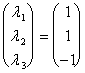
che è la 1ª colonna della matrice rappresentativa B rispetto alla base e1. Analogamente:
f(e21) =  avente come soluzioni:
avente come soluzioni: 
f(e31) =  avente come soluzioni:
avente come soluzioni: 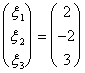
Pertanto la matrice rappresentativa rispetto alla nuova base è.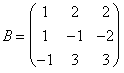 le cui colonne sono i vettori f(e11) , f(e21) , f(e31) .
le cui colonne sono i vettori f(e11) , f(e21) , f(e31) .
