Geometria Euclidea dello spazio
1) Calcola il prodotto scalare ![]() :
:
(2*1) + (3*-1) + (1*0) = -1
2) Calcola il prodotto vettoriale ![]() e dire cosa individua:
e dire cosa individua:
Il prodotto vettoriale è una operazione valida esclusivamente in Â3 ed il cui significato è di trovare un vettore che sia ortogonale ad entrambe i vettori precedenti , nel nostro caso è ![]() .
.
3) Cosa è e come varia l´orientazione nello spazio scambiando i vettori :
Si tratta del determinante della matrice avente quali vettori colonna i 3 vettori dei quali valutare l´orientazione. Si parla di orientazione positiva nel caso che i 3 vettori possono esser rappresentati da medio indice e pollice della mano destra e di orientazione negativa nel caso in cui sono rappresentati dagli stessi diti ma della mano sinistra.
4) Che cosa è un parallelogramma e che cosa è un parallelepipedo :
Un parallelogramma è un quadrilatero che giace sul piano avente i lati a due a due paralleli. Un parallelepipedo è invece la unione di 2 parallelogrammi situati su 2 piani paralleli.
5) Come varia il volume di un parallelepipedo se ad un vettore sostituiamo la somma di un multiplo di un altro vettore :
Non cambia minimamente in quanto il volume del parallelepipedo è pari al determinante della matrice avente come vettori colonna 3 spigoli concorrenti, è pertanto chiaro che alterando nella maniera descritta tale matrice , per le regole sul determinante, il determinante stesso non varia.
5) Come ottenere un vettore di lunghezza unitaria :
Si tratta semplicemente di dividerlo per la sua norma ![]()
6) Come valutare la area di un triangolo di vertici O , x = ![]() , y =
, y = ![]() :
:
Si tratta di un triangolo che giace su un piano e pertanto la sua area non ne tiene conto della particolare posizione spaziale, il metodo più rapido per calcolare tale area è utilizzare la formula ![]() dove a è la angolo compreso tra i 2 vettori il cui valore si può calcolare tramite il prodotto scalare
dove a è la angolo compreso tra i 2 vettori il cui valore si può calcolare tramite il prodotto scalare ![]() .
.
7) Quanti modi esistono per individuare una retta nello spazio :
1) intersezione di 2 piani espressi in forma cartesiana
2) Retta passante per un punto lungo la direzione individuata da un vettore ad essa parallelo.
Come si passa dalla rappresentazione cartesiana di una retta nello spazio alla rappresentazione parametrica ?
Si ricava in termini di span risolvendo il sistema omogeneo di 2 equazioni in 3 incognite.
8) Come si passa dalla rappresentazione parametrica di una retta nello spazio alla rappresentazione cartesiana :
Si scrive l´equazione del punto generico, si isola t per le 3 equazioni ricavate e poi si eguagliano 2 a 2 , il risultato sono le 2 equazioni cartesiane dei piani la cui intersezione è la retta.
9) Quando 2 rette sono sghembe :
Quando non esiste alcun piano che le contiene entrambe.
10) Come si valuta la distanza tra 2 rette sghembe :
Si valuta la distanza tra un punto di una ed il piano ad essa parallelo contenente la 2ª retta , si ricava una equazione cartesiana di tale piano ottenendo un vettore ad esso normale dato dal prodotto vettoriale dei vettori direttori delle 2 rette e per trovare il coefficiente d si impone che il piano passi per lo stesso punto evidenziato nella equazione generica della 2ª retta. A tal punto si valuta la distanza del punto dal piano tramite la formula ![]()
11) Quanti modi esistono per individuare un piano nello spazio :
1) Quale span di 2 vettori direttori e passante per un punto dato.
2) Piano passante per 3 punti dati.
3) Piano espresso da una equazione cartesiana.
12) Come si passa dalla rappresentazione cartesiana di un piano alla rappresentazione parametrica :
Si risolve semplicemente il sistema costituito da una unica equazione in 3 variabili e che quindi esprimerà le soluzioni quale span di 2 vettori direttori, è la forma parametrica.
13) Come si passa dalla rappresentazione parametrica di un piano alla rappresentazione cartesiana :
Si scrive il vettore ortogonale al piano quale prodotto vettoriale tra i 2 vettori direttori, le sue coordinate corrispondono ai coefficienti delle incognite nella equazione del piano, per ricavare il termine noto si sostituisce a tale equazione un punto per il quale il piano deve passare.
14) Come si calcola la retta intersezione se due piani sono espressi da equazioni cartesiane :
Si risolve il sistema lineare costituito dalle 2 equazioni dei piani, essendo 2 equazioni in 3 incognite le soluzioni si esprimeranno quale span di 1 vettore.
15) Come si calcola la retta intersezione se due piani sono espressi da equazioni parametriche :
Si passa alla corrispondente rappresentazione parametrica e si procede come sopra.
16) Come si calcola l´intersezione di due rette espresse da equazioni parametriche :
Si scrive il punto generico di entrambe le rette li si eguaglia, si trovano così i valori dei parametri per i quali le 2 rette si intersecano tali valori sostituiti nei rispettivi punti generici debbono restituire lo stesso punto che poi è il punto di intersezione delle 2 rette.
17) Come si calcola l´intersezione di due rette espresse da equazioni cartesiane :
Si passa alla rappresentazione parametrica e si procede come sopra.
18) Cosa è un vettore normale ad un piano e qual´ è il suo utilizzo principale :
È un vettore avente come coordinate i coefficienti dei termini x , y , z del piano. È utile per determinare la retta intersezione di 2 piani ed in altre applicazioni.
19) Come si trova la intersezione tra un piano in forma cartesiana ed una retta in forma parametrica :
Si sostituisce il punto generico della retta alle rispettive coordinate del piano e si isola in tal modo il valore del parametro nel punto di intersezione che sostituito nel punto generico restituisce il punto d´intersezione stesso.
20) Quale è la formula che esprime la distanza tra un punto ed un piano :
![]()
21) Come si calcola la proiezione ortogonale di un punto su di un piano :
Si calcola quale intersezione tra il piano e la retta passante per il punto avente quale vettore direttore un vettore ortogonale al piano.
Condizioni di ortogonalità e parallelismo tra piani e rette
22) Quando due piani sono paralleli :
Quando hanno vettori ortogonali uguali o multipli.
23) Quando due piani sono ortogonali :
Quando il prodotto scalare dei 2 vettori ortogonali è 0.
24) Quando due rette sono parallele :
Quando i loro vettori direttori sono uguali o multipli e le rette passano per 2 diversi punti del piano.
25) Quando due rette sono ortogonali :
Quando il prodotto scalare dei 2 vettori direttori è 0.
26) Quando una retta ed un piano sono paralleli :
Quando il prodotto scalare tra il vettore direttore della retta ed il vettore ortogonale al piano è 0.
27) Quando una retta ed un piano sono ortogonali :
Quando il vettore direttore della retta è uguale o multiplo del vettore ortogonale al piano.
Rotazioni e simmetrie di R3
28) Quale matrice è associata ad una rotazione di R3 intorno al vettore e1 :
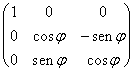
29) Come effettuare una rotazione intorno ad una retta qualsiasi dello spazio :
La retta deve essere orientata, e la sua direzione e verso debbono essere indicati da un versore ad essa parallelo, intorno a questo versore si costruisce una base ortonormale, il secondo versore si trova ortogonale al 1° ed il terzo vettore quale prodotto vettoriale tra i primi due vettori. Si normalizzano i 3 versori e si riuniscono a formare le colonne di una matrice ortogonale. Si esegue la rotazione intorno a v come se fosse e1, cioè con la matrice 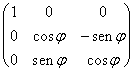 dopodichè il risultato si riporta nella base canonica tramite la matrice ortogonale di cambiamento di base appena costruita.
dopodichè il risultato si riporta nella base canonica tramite la matrice ortogonale di cambiamento di base appena costruita.
30) Come ricavare le formule di una simmetria rispetto ad un piano arbitrario p :
Si trova il vettore ortogonale al piano e si sostituisce il suo valore generico nella equazione del piano isolando in tal modo il valore del parametro t = tp ed osservando che nel punto da simmetrizzare il parametro è t = 0 segue che il parametro nel punto simmetrizzato non può che valere 2* tp , si sostituisce questo valore del parametro al punto generico della retta e si ottiengono le equazioni del generico punto simmetrizzato.
31) Come ricavare le formule della riflessione di un punto p rispetto ad un punto q :
Si osserva che il punto q si trova esattamente a metà tra il punto p e la sua simmetria Up pertanto deve essere ![]() e dunque 2q = p + Up edunque Up = 2q - p che è l´equazione del punto p simmetrizzato.
e dunque 2q = p + Up edunque Up = 2q - p che è l´equazione del punto p simmetrizzato.
