Teoremi sui limiti
Limiti di funzioni
1) Unicità del limite :
Descrizione : se ![]() e
e ![]() Þ l1 = l2
Þ l1 = l2
se fosse l1 ¹ l2 dovrebbero esistere un intorno di l1 ed un intorno di l2 tra loro distinti ai quali dovrebbero corrispondere 2 intorni distinti di x0 cosa che invece non può accadere visto che l´intersezione di 2 intorni di x0 è ancora un intorno di x0 e conterrà almeno un punto di x ¹ x0 in quanto x0 è un punto di accumulazione (quindi ogni intorno di x0 contiene almeno un punto del dominio X diverso da x0). In definitiva quindi l´intersezione di 2 intorni è non vuota contro l´ipotesi fatta.
2) Teorema della permanenza del segno :
Descrizione : se ![]() allora f(x) > 0 definitivamente per x ® x0 dove il termine definitivamente indica che la proprietà è valida per ogni x appartenente ad almeno un intorno di x0 con x ¹ x0 .
allora f(x) > 0 definitivamente per x ® x0 dove il termine definitivamente indica che la proprietà è valida per ogni x appartenente ad almeno un intorno di x0 con x ¹ x0 .
Se 0 < l < +¥ allora scegliendo e = l si fa in modo che l´intorno V di l sia (0 , 2l) e per questo intorno avremo un intorno di x0 nel quale la funzione è compresa tra 0 e 2l.
Occhio : Il fatto che una funzione sia > 0 non implica che lo sia anche il suo limite, ad esempio x2 è definitivamente maggiore di 0 per x®0 (il definitivamente esclude il punto x0 = 0 dove x2 = 0) però ![]()
Miglioria dim. : Se 0 < l < +¥ allora scegliendo e = l - m si fa in modo che l´intorno V di l sia (m , 2l - m) e quindi si può estendere il teorema dicendo che esso è valido per ogni 0 < m. < l , ossia non esiste un solo intorno ma ne esiste uno per ogni m scelto tra 0 ed l.
3) Rapporto tra l´esistenza di un limite finito e la limitatezza della funzione :
Descrizione : Se per una funzione esiste un limite finito per x®x0 Þ la funzione è definitivamente limitata per x®x0
ma non è detto che se la funzione è limitata allora ammette un limite finito, ad esempio sgnx è una funzione limitata ma non esiste il limite per x ® 0.
4) Teorema del confronto :
Descrizione : Se ho 2 funzioni f(x) e h(x) aventi lo stesso limite l per x ® x0 ed una terza funzione g(x) è definitivamente compresa tra h(x) e f(x) per x ® x0 allora anche g(x) tende allo stesso limite l.
Per ogni intorno V di l dovrà esistere un intorno U1 di x0 per il quale f(x) Î V ed un intorno U2 di x0 per il quale h(x)ÎV , ebbene per ogni x appartenente alla intersezione di questi 2 intorni si avrà che sia f(x) che h(x) apparterranno a V e pertanto anche la g(x) che è tra esse compresa.
Esempio : calcolo del limite di sinx / x.
5) Quanto vale il limite del prodotto tra f(x) avente limite l1 e g(x) avente limite l2 ?
Descrizione : f(x)*g(x) ha come limite l1*l2 .
Affinchè sia vera deve essere | f(x)*g(x) - l1*l2 | < e il che si ottiene a partire dalla espressione f(x)g(x) con le seguenti :
1) Si scrive f(x)g(x) - l1l2 = f(x)g(x) - l1l2
2) Si aggiunge e toglie al 2° membro l1*g(x) .
3) Raccogliendo si giunge alla forma f(x)*g(x) - l1*l2 = g(x)*( f(x) - l1 ) + l1*( g(x) - l2 )
4) Si osserva che entrambe i termini tra parentesi per definizione di limite sono minori di e e che g(x) possedendo un limite finito è una funzione limitata pertanto è |g(x)| < M per x ® x0 . La disuguaglianza si riduce pertanto alla forma | f(x)*g(x) - l1*l2 | < Me + l1*e che data la arbitrarietà di e conferma la assunto.
6) Quanto vale il limite della funzione1/g(x) avente limite l1 > 0 ?
Descrizione : 1 / g(x) ha come limite 1 / l1 .
Affinchè sia vera deve essere | 1/g(x) - 1/ l1 | < e il che si ottiene a partire dalla | 1/g(x) - 1/ l1 | effettuando il minimo comun denominatore che restituisce ![]() il numeratore del 2° membro risulta minore di e per definizione di limite mentre al denominatore, in virtù del teorema della permanenza del segno, sappiamo che, avendo g(x) limite positivo, è sicuramente g(x)> m > 0 per x®x0 quindi possiamo scrivere
il numeratore del 2° membro risulta minore di e per definizione di limite mentre al denominatore, in virtù del teorema della permanenza del segno, sappiamo che, avendo g(x) limite positivo, è sicuramente g(x)> m > 0 per x®x0 quindi possiamo scrivere ![]() in quanto il denominatore non può annullarsi e quindi tramite e possiamo rendere piccola quanto vogliamo la differenza tra il limite e la funzione.
in quanto il denominatore non può annullarsi e quindi tramite e possiamo rendere piccola quanto vogliamo la differenza tra il limite e la funzione.
7) Sotto quali condizioni è possibile calcolare il limite di una funzione composta ?
Descrizione : Se ![]() ed f(x) ¹ l definitivamente per x®x0 e
ed f(x) ¹ l definitivamente per x®x0 e
se ![]() allora si ha che
allora si ha che ![]()
Si dimostra a ritroso affermando che esiste un intorno W di k per il quale esiste un intorno V di l i cui elementi y sono tali che g(y) è compreso in W. Si compie poi un altro passo a ritroso allo scopo di trovare un intorno di x0 composto da x tali che f(x) ha valori su tutto V ad eccezione di l, tale intorno si trova quale intersezione tra l´intorno U1 di x0 composto da x tali che f(x) Î V e l´intorno U2 di x0 composto da tutte le x per le quali f(x) ¹ l .
8) Considerazioni sui limiti delle funzioni monotone :
Descrizione : Una funzione monotona ammette sempre il limite ed in particolare esso coincide con il Sup f(x) se la funzione è crescente e noi consideriamo un intorno sinistro di x0 , mentre coincide con l´ Inf f(x) se la funzione è crescente e noi consideriamo un intorno destro di x0.
Dimostrare che se x è crescente allora il limite è il Sup se consideriamo un intorno sinistro di x0 significa considerare entrambe i casi possibili, ossia definendo Sup f := l si ha :
a) l Î Â
Per definizione di estremo superiore si ha :
* f(x) £ l " x compresa tra -¥ ed xo
* Per ogni e > 0 esiste un xe tale che f(x)+e > l e quindi l non è più estremo superiore
Essendo la funzione crescente avremo evidentemente che " x compresa tra xe ed x0 si ha che l-e < f(x) £ l ossia l è il limite di f per x che tende ad x0 .
b) l = + ¥
La f in questo caso non è limitata superiormente quindi dovremo prendere come riferimento un valore M della funzione e dire che per le x a destra della xM associata al punto M dato che la funzione è crescente si ha che f(x) > M e dunque il limite è +¥ . Se la funzione non fosse stata crescente nulla avremmo potuto dire.
Limiti di successioni a valori in Â
9) Una successione convergente è limitata.
Dato che una successione non è che una particolare funzione, segue che per essa vale il teorema 29) secondo il quale se per una funzione esiste un limite finito per x®x0 Þ la funzione è definitivamente limitata per x®x0 si avrà pertanto che per gli n maggiori di un certo N, | an | £ M0 che si comporta da estremo superiore mentre per le n comprese tra 0 ed N dovrà esistere un massimo M1 per | an | in quanto essi rappresentano un sottoinsieme finito di Â. In definitiva dunque la successione an è limitata dal massimo tra M0 ed M1 .
10) Una successione monotona e limitata è convergente.
11) Teorema ponte tra i limiti di funzioni ed i limiti di successioni :
Descrizione : ![]() Û
Û ![]() " successione an a valori in X \ {x0}e convergente a x0
" successione an a valori in X \ {x0}e convergente a x0
Þ Dovendo valere il 1° membro allora preso un e >0 esisterà un d > 0 tale che per ogni x che disti da x0
0<|x - x0| < d si ha che | f(x)-l |< e e dato che la successione an converge ad x0 , allora esisterà un valore N tale che " n > N si ha che | an - x0 | < d e pertanto si avrà che | f(an) - l | < e per ogni n > N.
Ü Si procede negando il 1° membro ed ottenendo che anche il 2° membro è falso, in particolare la negazione afferma che $ un e tale che per ogni d > 0 esiste xd Î X tale che 0 < | xd - x0 | < d e | f(xd) - l | ³ e . A questo punto si fa tendere progressivamente d a 0 ad esempio dandogli i valori 1, 1/2, 1/3, ... , 1/n e per ogni d si rileva il valore xd per il quale | f(x) - l | ³ e . Abbiamo in definitiva creato una successione che tende ad x0 ma la cui immagine non tende ad l il tutto come conseguenza della ipotesi assurda iniziale che ![]() .
.
12) Dimostrare che ![]() " aÎÂ , a > 1
" aÎÂ , a > 1
Sfruttando il teorema ponte possiamo invece dimostrare che " successione bn ® +¥ si ha che ![]() . Infatti :
. Infatti :
![]()
l´ultimo termine si riduce a 0 * a = 0 in virtù del ![]() e dunque è dimostrato che
e dunque è dimostrato che ![]() .
.
Per dimostrare che ![]() occorre riportarlo alla forma
occorre riportarlo alla forma ![]() che dimostreremo essere ugule a 0 per n ® +¥ , ciò si ottiene raccogliendo come potenza 2a
che dimostreremo essere ugule a 0 per n ® +¥ , ciò si ottiene raccogliendo come potenza 2a 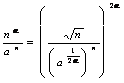 . Per dimostrare infine che
. Per dimostrare infine che ![]() ® 0 per x ®+¥ si pone h = a - 1 e si disuguaglia tramite Bernoulli poi dal teorema del confronto si desume che
® 0 per x ®+¥ si pone h = a - 1 e si disuguaglia tramite Bernoulli poi dal teorema del confronto si desume che ![]() ® 0 per x® +¥.
® 0 per x® +¥.
Proprio la aver utilizzato questa disuguaglianza che prevede n Î À ci ha costretto ad utilizzare [bn ] + 1 .
13) Dimostrare che e è il Sup della successione ![]() naturalmente per n ® +¥ con n Î À \ {0}.
naturalmente per n ® +¥ con n Î À \ {0}.
Occorre dimostrare che la successione an è convergente, il che avviene per ogni successione monotona e limitata, dimostreremo quindi che an è crescente e limitata.
an è crescente Þ Si dimostra verificando che il rapporto an / an -1 è maggiore di 1 il che si ottiene riportando il numeratore ad una forma del tipo (1 + h)n e quindi disuguagliando tramite Bernoulli . Il risultato ottenuto è valido solo per n ³ 2 in quanto per n = 1 si giunge all´errore logico 01 .
an è limitata Þ Si dimostra analogamente su di una successione ![]() e verificando che il rapporto bn / bn -1 è minore di 1 il che si ottiene riportando il numeratore ad una forma del tipo (1 + h)n e quindi disuguagliando tramite Bernoulli .
e verificando che il rapporto bn / bn -1 è minore di 1 il che si ottiene riportando il numeratore ad una forma del tipo (1 + h)n e quindi disuguagliando tramite Bernoulli .
Si può pertanto affermare che an è compresa tra 0 e bn la quale del resto tende allo stesso limite infatti si ha che se ![]() Þ
Þ ![]()
Dando un valore ad n si ha un intervallo dato dai valori assunti da an e da bn nel quale è compreso e .
14) Dimostrare che è anche ![]() quindi non solo per n Î À\{0}
quindi non solo per n Î À\{0}
15) Una successione limitata a valori in  ha una sottosuccessione convergente.
Si possono verificare 2 casi :
a) un elemento a compare infinite volte e pertanto la sottosuccessione bn converge ad a
b) L´immagine della successione è un insieme infinito (in quanto la successione contiene infiniti valori diversi) e limitato (in quanto la successione è limitata) pertanto per il teorema di Bolzano-Weierstass ammette almeno un punto di accumulazione l Î Â. Ogni intorno di l contiene infiniti valori della successione pertanto si può creare una sottosuccessione che tende ad l, in particolare siano gli intorni ![]() che per n®+¥ Un®l
che per n®+¥ Un®l
la sottosuccessione si ricava scegliendo " nÎÀ quale elemento della successione an rientra in Un , in tal modo si crea una sottosuccessione convergente a partire da una successione che potrebbe non esserlo.
16) Una successione fondamentale è limitata.
Una successione è fondamentale se " e >0 esiste un N Î À tale che presi 2 qualsiasi elementi n ed m maggiori di N nel dominio À della successione si ha che | an - am | < e. Per dimostrare che tale successione è limitata occorre tener conto che per gli n compresi tra 0 ed N esiste un massimo M0 per i valori assunti da an in quanto essi costituiscono un sottoinsieme finito di Ân. Per gli n ³ N invece si può maggiorare |an | tramite Cauchy-Schwarz infatti si ha
|an| = | (an - aN) + aN | £ | (an - aN) | + | aN | quindi scegliendo m = N ed arbitrariamente ponendo e = 1 si ottiene che per ogni n ³ N si ha che |an | £ 1 + |aN| = M1 , in definitiva dunque an è limitata dal massimo tra M0 ed M1 .
17) Criterio di Cauchy.
Descrizione : Una successione a valori reali è convergente Û è fondamentale
Þ Dimostrare che una successione è fondamentale significa dimostrare che " e >0 esiste un N Î À tale che presi 2 qualsiasi elementi n ed m maggiori di N nel dominio À della successione si ha che | an - am | < e. Per far ciò si aggiunge e sottrae l all´interno del modulo e si disuguaglia tramite Cauchy-Schwarz ottenendo che :
| an - am | £ | an - l | + | am - l | < e infatti dalla convergenza della successione ossia ![]() segue che dato un e >0 esisterà un N oltre il quale | an - l | < e / 2 e sostituendo tale risultato nella disuguaglianza ottenuta con Cauchy-Schwarz il teorema risulta dimostrato.
segue che dato un e >0 esisterà un N oltre il quale | an - l | < e / 2 e sostituendo tale risultato nella disuguaglianza ottenuta con Cauchy-Schwarz il teorema risulta dimostrato.
Ü Occorre sfruttare i 2 seguenti teoremi:
a) Una successione fondamentale è limitata
b) Una successione limitata a valori in  possiede sempre una sottosuccessione akn convergente ad l.
Dimostriamo la convergenza di an ossia che | an - l | £ e sfruttando il fatto che akn converge ad l, quindi aggiungiamo e sottraiamo akn nel modulo ed applicando la disuguaglianza triangolare, si ottiene
| an - l | £ | an - akn | + | akn - l | £ e .Il 2° membro è minore di e in quanto per ogni n ³ N1 si avrà che
| aKn - l | < e / 2 mentre per definizione di successione fondamentale è |an - am| < e / 2 per n, m ³ N2 e ponendo
m = kn si ha che |an - akn | < e / 2 per n > N 2 .
Insieme compatto
44) Sia K Í Ân allora K è compatto Û K è chiuso e limitato
Þ K compatto implica che ogni successione a valori in K ha una sottosuccessione che tende ad x Î K pertanto K è chiuso in quanto contiene i suoi punti di accumulazione. La limitatezza di K si dimostra per assurdo affermando che se vi fosse una successione non limitata che tende a ¥, ogni sua sottosuccessione avrebbe limite ¥ e pertanto non è vero che ogni sottosuccessione tende ad un elemento x Î K e quindi non ci troveremmo su di un compatto.
Ü * K limitato implica che ogni successione aK a valori in K sia limitata
* Ogni successione limitata possiede una sottosuccessione convergente ad un elemento lÎÂn , tale elemento l è punto di accumulazione per K e pertanto o è punto interno o è punto di frontiera, e siccome K chiuso vuol dire che contiene sia i punti interni che i punti di frontiera, ne consegue che K contiene anche l ed in definitiva abbiamo provato che K è compatto, ossia che ogni successione a valori in K ha una sottosuccessione che tende ad lÎK.
