Antenne

1) Circuito a costanti distribuite :

Si parla di circuito a costanti distribuite quando il rapporto tra la lunghezza della linea e la velocità della luce è circa dello stesso ordine di grandezza delle variazioni temporali considerate significative. Se invece le variazioni temporali sono molto più lente, è sufficiente l'analisi tramite il circuito a costanti concentrate.

2) Equazioni generali delle linee :

Assemblando le impedenze longitudinali in una unica impedenza ad unità di lunghezza e le ammettenze trasversali in una unica ammettenza ad unità di lunghezza  si può scrivere   da cui   , ed analogamente   da cui   .

3) Soluzione delle equazioni generali delle linee :

Derivando rispetto da x la  si ottiene  , ponendo la soluzione di questa equazione è . Analogamente derivando rispetto ad x la  si ottiene  la cui soluzione è  la quale può anche essere scritta in funzione di  semplicemente sostituendo nella  , si ha infatti    nella quale uguagliando i coefficienti degli esponenziali omologhi si ha    ed analogamente si trova

 dove Z₀ è detta impedenza caratteristica della linea. Pertanto le soluzioni delle equazioni delle linee sono :

4) Costante di propagazione della linea :

5) Impedenza caratteristica :

6) Linea adattata :

Si tratta di una linea chiusa su di una impedenza pari alla sua impedenza caratteristica, la condizione di chiusura sul carico è quindi   sostituendo in essa le equazioni      e      si ottiene    e quindi   , sfruttando quest'ultima (.che sostanzialmente indica l'assenza dell'onda regressiva) e la condizione di chiusura all'ingresso sul generatore, si ha   , in definitiva le equazioni nel caso di linea adattata sul carico sono   e   . Analogamente se il generatore V_g viene posto alla fine della linea ed il carico Z₀ all'inizio, si ha che  e quindi si ha soltanto l'onda regressiva.

7) Impedenza nel caso di linea adattata :

Quando la linea è adattata l'impedenza che si vede verso il carico in un qualsiasi punto della linea stessa è sempre uguale all'impedenza caratteristica. Si dimostra osservando che nel caso di onda progressiva il rapporto 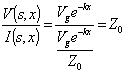 è costante, se invece consideriamo la linea adattata in ingresso si ha -Z₀ .

8) Impedenza normalizzata sul generatore e sul carico :

9) Coefficiente di riflessione sul generatore e sul carico :

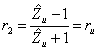
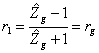
10) Equazione delle linee in regime permanente :

Si possono sostituire i fasori nelle equazioni che avevamo trovato nel dominio di Laplace

L'espressione nel tempo di v(t,x) si ottiene ricordando che essa equivale alla parte reale del fasore rotante ossia

si nota quindi la presenza di un'onda progressiva e di un'onda regressiva, imponendo che l'argomento del coseno sia costante (...uguagliando a 0 il differenziale) si trova la velocità di fase   per l'onda progressiva e   per l'onda regressiva.

11) Valore del coefficiente di riflessione all'ascissa x della linea  :

12) Rapporto d'onda stazionaria r :

La tensione lungo la linea è  che può anche essere scritta in funzione del coefficiente di riflessione sul carico r₂ infatti raccogliando  si ha 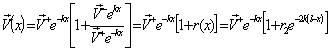. Osservando che i coefficienti di riflessione sono tutti compresi tra 0 ed 1, l'origine per essi si può prendere nel centro della carta di Smith dove si ha l'adattamento e quindi il coefficiente di riflessione deve valer 0. In tal modo si può quindi avere una espressione grafica di  e determinarne il valore massimo  ed il valore minimo definendo in tal modo l'importante parametro  .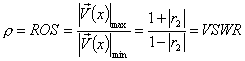

In particolare si ha che se la linea è adattata ROS=1 mentre se è disadattata ROS=¥ e questo come conseguenza del fatto che il coefficiente di riflessione sul carico può assumere solo valori compresi tra 0 ed 1 essendo il rapporto tra l'onda incidente e l'onda riflessa.

13) Larghezza di lobo :

E' l'angolo compreso tra le due direzioni a cui il diagramma di radiazione in campo si riduce a 0.707 del valore massimo.

14) Realizzazione pratica di antenna a dipolo :

Da un punto di vista costruttivo è molto difficile spezzare in due l'antenna mantenendo le proprietà di resistenza meccanica, pertanto si utilizza soltanto mezza antenna e la restante è come se ci fosse a patto di inserire sulla superficie un piano metallico che quindi ottempera alla condizione al contorno secondo la quale il campo elettrico deve essere nullo in corrispondenza della superficie di discontinuità.

15) Tipologie di antenne ad apertura :

• antenne a tromba nelle quali la guida aumenta gradualmente la propria sezione al fine di adattare lo spazio libero al modo dominante presente nella guida
• antenne a riflettore in cui la guida d'onda termina ancora su di una tromba, detta illuminatore la quale si trova nel fuoco di un paraboloide metallico verso cui irradia ottenendo in tal modo un'onda piana.

16) Costante dielettrica nel vuoto :

17) Permeabilità magnetica nel vuoto :

18) Attenuazione di trasmissione nello spazio libero :

essa pertanto aumenta con il quadrato della frequenza, ma essendo in genere la banda molto più piccola della frequenza portante, si può supporre che l'attenuazione di trasmissione sia pressochè costante in banda.

19) Parametri di un'antenna :

Un immaginario radiatore isotropico irradia potenza in tutte le direzioni, a distanza r da esso la densità di potenza è  , una antenna reale viene confrontata ad esso mediante la funzione di guadagno   il cui valore massimo è chiamato guadagno d'antenna G, molto utilizzato nelle applicazione è anche l'EIRP = PG .

Per un'antenna ricevente la potenza ricevuta è funzione della densità di potenza  che agisce su di essa e dell'area equivalente A_e , si ha cioè . Ed è caratterizzata da un guadagno di ricezione .

20) Attenuazione dovuta alla pioggia :

vale circa 1dB/Km in condizioni di pioggia intensa a 10GHz e può arrivare sino a 8dB/Km nelle stesse condizioni a 30GHz.

21) Effetto pellicolare :

Nei conduttori ideali s è infinita e la densità di corrente è non nulla solo sulla superficie di separazione e diretta assialmente, nei conduttori reali s è molto elevata ma finita pertanto si ha che la densità di corrente è non nulla anche all'interno del conduttore ma decresce esponenzialmente allontanandosi dalla superficie, in particolare la distanza alla quale j si riduce ad 1/e del suo valore sulla superficie è chiamata spessore di penetrazione  e diminuisce al crescere della frequenza, in particolare per f > 10kHz si ha che d_m è maggiore delle dimensioni del conduttore.

22) Relazione tra i parametri primari ed i parametri secondari :

si osserva comunque che in entrambe le equazioni g è trascurabile nelle somme in quanto infinitesima.