Trasformata Z
1) Relazione tra trasformata di Laplace, trasformata di Fourier e trasformata Z :
Nel caso di sistemi tempo - continui la trasformata di Laplace generalizza la trasformata di Fourier mentre nel caso di sistemi tempo - discreti la trasformata Z generalizza la trasformata di Fourier.
2) Trasformata Z di una sequenza x[n] :
![]() essendo
essendo ![]() una variabile complessa si ottiene che la trasformata Z coincide con la trasformata di Fourier unicamente sul cerchio unitario. La condizione di convergenza è
una variabile complessa si ottiene che la trasformata Z coincide con la trasformata di Fourier unicamente sul cerchio unitario. La condizione di convergenza è ![]() pertanto la trasformata Z può convergere anche in casi in cui la trasformata di Fourier non converge.
pertanto la trasformata Z può convergere anche in casi in cui la trasformata di Fourier non converge.
3) Convergenza della serie ![]() :
:
- Se
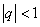 si ha
si ha 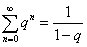
4) Trasformata Z di una sequenza a lunghezza finita :
![]() con n1 ed n2 interi, si ha che la regione di convergenza è almeno
con n1 ed n2 interi, si ha che la regione di convergenza è almeno ![]() e può includere anche gli estremi, in particolare :
e può includere anche gli estremi, in particolare :
- Se
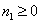 è compreso anche il punto
è compreso anche il punto 
- Se
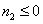 è compreso anche il punto 0
è compreso anche il punto 0
5) Trasformata Z di una sequenza monolatera destra :
Si tratta di sequenze nulle per n < n1 , pertanto la trasformata Z è ![]() e la regione di convergenza è l'esterno di un cerchio inoltre si ha che :
e la regione di convergenza è l'esterno di un cerchio inoltre si ha che :
- Se la sequenza è causale la regione di convergenza comprende
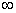 e viceversa
e viceversa - Se la regione di convergenza è l'esterno di un cerchio allora la sequenza è monolatera destra e viceversa
6) Trasformata Z di una sequenza monolatera sinistra :
Si tratta di sequenze nulle per n > n2 , pertanto la trasformata Z è ![]() , mediante il cambio di variabile
, mediante il cambio di variabile ![]() ci si riporta al caso delle sequenze monolatere destre ne deriva pertanto che la regione di convergenza è l'interno di un cerchio.
ci si riporta al caso delle sequenze monolatere destre ne deriva pertanto che la regione di convergenza è l'interno di un cerchio.
7) Trasformata Z di una sequenza bilatera :
Sono sequenze che si estendono da -![]() a +
a +![]() , possono essere trattate come la somma di una monolatera destra e di una monolatera sinistra
, possono essere trattate come la somma di una monolatera destra e di una monolatera sinistra ![]() , la regione di convergenza della trasformata è l'intersezione delle due regioni di convergenza individuate per le due sequenze costituenti, si tratta pertanto di uno o più anelli circolari.
, la regione di convergenza della trasformata è l'intersezione delle due regioni di convergenza individuate per le due sequenze costituenti, si tratta pertanto di uno o più anelli circolari.
8) Teorema integrale di Cauchy :
![]()
essendo C un contorno chiuso che circonda l'origine e che è percorso in senso antiorario.
9) Trasformata Z inversa :
![]()
Essendo c un contorno chiuso situato intorno all'origine e compreso nella regione di convergenza di ![]() .
.
10) Trasformata Z inversa di funzioni razionali :
![]() = somma dei residui di
= somma dei residui di ![]() nei poli interni a c .
nei poli interni a c .
11) Calcolo dei residui per una funzione razionale :
Una funzione razionale può esprimersi nella forma 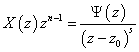 dove
dove ![]() non ha poli in
non ha poli in ![]() .
.
Nel caso si abbia un polo di ordine s = 1 in ![]() il residuo vale
il residuo vale ![]() mentre se si ha un polo di ordine s > 1 in
mentre se si ha un polo di ordine s > 1 in ![]() il residuo vale
il residuo vale 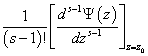 .
.
12) Trasformata Z inversa di funzioni serie di potenze :
Se la trasformata Z è in forma di una serie di potenze allora la sequenza x[n] coincide con il coefficiente di ![]() della serie di potenze.
della serie di potenze.
13) Trasformata Z inversa calcolata mediante espansione in fratti semplici :
La X(z) può essere scritta come sommatoria di fratti più semplici ciascuno dei quali ha al denominatore l'espressione di un polo semplice o multiplo mentre al numeratore c'è il corrispondente residuo nel polo stesso.
14) Proprietà della trasformata Z :

