Spettro del Campionamento

1) Processo di campionamento :

E' il prodotto tra un segnale di energia x(t) ed un treno di impulsi rettangolari ciascuno con durata τ

                                essendo                               

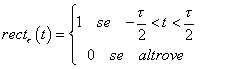
Il segnale campionato è pertanto:

ed il suo spettro:

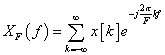         esiste a patto che        .

essendo  la sequenza dei campioni del segnale originario, essa può essere ricostruita a partire dallo spettro  mediante la .

2) Relazione tra lo spettro del segnale continuo e lo spettro del segnale campionato :

ossia lo spettro  del segnale campionato  è la somma di infinite repliche dello spettro del segnale x(t).

3) Come ricostruire il segnale originale a partire dal segnale campionato :

Nel dominio della frequenza si moltiplica per un rettangolo che taglia via le repliche dello spettro, la risposta impulsiva di un tale quadripolo è una sinc pertanto nel dominio del tempo si ha la convoluzione tra i campioni del segnale e la sinc.

4) Teorema di Shannon :

Un segnale può essere correttamente campionato e successivamente ricostruito a partire dai suoi campioni a patto che sia limitato in banda e venga campionato ad una frequenza doppia rispetto alla massima frequenza presente nel suo spettro.

5) Errore di quantizzazione :

Avendo N bit disponibili ed una escursione da -V_max a +V_max il quanto elementare vale  , l'errore di quantizzazione è pertanto compreso nell'intervallo  e la varianza è    .

6) Relazioni tra dominio del tempo e della frequenza :

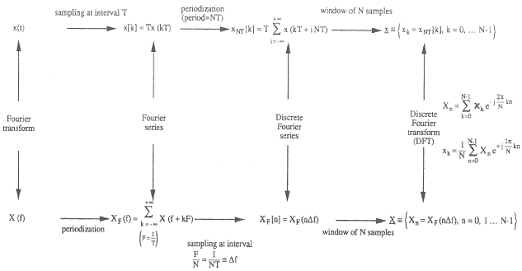
7) Finestre temporali :

Moltiplicando x(t) per una finestra temporale w(t) che vale 1 per 0 < t < NT e che quindi ha spettro

ne risulta che la risoluzione dello spettro calcolato tramite DFT è limitato dalla larghezza del lobo principale di W(f), inoltre abbassando i lobi laterali di W(f) con un'opportuna legge di dosaggio si ha un allargamento ed abbassamento del lobo principale rispetto alla finestra rettangolare.

8) Finestre frequenziali :

Un filtro antialiasing ideale è una finestra rettangolare applicata allo spettro del segnale nell'intervallo di Nyquist, ne consegue che campionando x(t) con passo  non si ha il ripiegamento dello spettro. Se invece x(t) ha componenti in frequenza all'esterno della banda di Nyquist ne consegue che lo spettro è alterato dalla finestratura, nel dominio del tempo si ha infatti la convoluzione con la funzione .

9) Trasformata di Fourier Discreta (DFT) :

   essendo                               

Mentre la sua trasformata inversa, la IDFT è:

10) Proprietà di linearità della DFT:

11) Proprietà di traslazione circolare della DFT:

12) Proprietà di coniugio e ribaltamento della DFT:

13) Convoluzione circolare:

Date due sequenze x₁(n) ed x₂(n) lunghe N si definisce la loro convoluzione circolare:

essendo  la periodicizzazione di ossia la restrizione ad un periodo lungo N.

Ne deriva che la DFT della convoluzione circolare è .

La convoluzione circolare coincide con la convoluzione lineare a patto che ogni sequenza sia estesa in modo che la convoluzione circolare abbia lo stesso numero di campioni della convoluzione lineare.

14) FFT:

Fast Fourier Trasform, si tratta di una semplificazione della DFT basata sulla periodicità dei coefficienti  , è idonea nel caso che il numero di campioni N sia una potenza di 2 , la complessità si riduce da  a .