Strutture guidanti
Linee di trasmissione
1) Equazioni dei telegrafisti :
Si parte considerando un tratto di linea avente lunghezza infinitesima dz, essa presenterà R, L, C, G ad unità di lunghezza e si potranno pertanto scrivere le due equazioni ![]() e
e ![]() dalle quali semplificando si ottengono
dalle quali semplificando si ottengono ![]() e
e ![]() dalle quali si possono ottenere le equazioni dei telegrafisti
dalle quali si possono ottenere le equazioni dei telegrafisti ![]() e
e ![]() dove
dove ![]() è la costante di propagazione della linea.
è la costante di propagazione della linea.
![]()
2) Costanti primarie e secondarie :
le costanti primarie sono R, L, C, G mentre le costanti secondarie sono la costante di propagazione g e l´impedenza caratteristica ![]() essa si ricava scrivendo le generiche soluzioni delle equazioni dei telegrafisti ossia
essa si ricava scrivendo le generiche soluzioni delle equazioni dei telegrafisti ossia ![]() e
e ![]() e sostituendo la prima nella
e sostituendo la prima nella ![]() , si ottiene un´espressione che lega I(z) a V(z) mediante l´impedenza caratteristica.
, si ottiene un´espressione che lega I(z) a V(z) mediante l´impedenza caratteristica.
3) Lunghezza d´onda e velocità di fase :
L´onda diretta e quella riflessa si propagano lungo la linea, i punti nei quali ciascuna di esse assume la stessa fase si trovano tra loro a distanze multiple della lunghezza d´onda ![]() , i punti equifase si muovono lungo la linea con una velocità
, i punti equifase si muovono lungo la linea con una velocità ![]() .
.
4) Concetto di pupinizzazione :
Per variare le caratteristiche propagative di una linea si deve agire non tanto sulla geometria quanto inserendo degli elementi concentrati, induttanze o capacità, opportunamente distanziate.
5) Coefficiente di riflessione sul carico :
Considerando un sistema di coordinate in cui il carico ZL si trova in z = 0 ed alla sua sinistra si ha la linea avente lunghezza –l, e ricordando l´espressione di tensione e corrente alla coordinata z cioè ![]() e
e ![]() si ha
si ha ![]() da cui si può scrivere
da cui si può scrivere 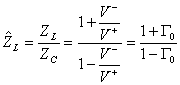 dove
dove 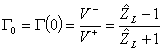 è il coefficiente di riflessione sul carico e
è il coefficiente di riflessione sul carico e ![]() l´impedenza normalizzata.
l´impedenza normalizzata.
6) Impedenza d´ingresso Zin di una linea lunga l chiusa su di un carico ZL con e senza perdite :
![]() dalla quale si sostituisce
dalla quale si sostituisce 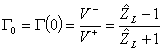 ed accoppiando opportunamente gli esponenziali si giunge alla espressione
ed accoppiando opportunamente gli esponenziali si giunge alla espressione 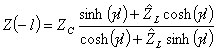 supponendo poi che la linea sia priva di perdite l´equazione si riduce a
supponendo poi che la linea sia priva di perdite l´equazione si riduce a ![]() .
.
7) Caratteristiche della Zin in funzione della lunghezza della linea :
Dalla ![]() è evidente che per multipli di l/2 si ha Zin = ZL mentre per multipli dispari di l/4 si ha
è evidente che per multipli di l/2 si ha Zin = ZL mentre per multipli dispari di l/4 si ha ![]() . Se il carico poi è in corto ossia ZL= 0 si ha che l´impedenza è puramente reattiva ed ha la andamento della tangente mentre nel caso il carico sia un circuito aperto l´impedenza è ancora puramente reattiva ma la andamento è quello della cotangente. Infine se ZL = ZC allora Zin = ZC per ogni l ossia la linea è adattata.
. Se il carico poi è in corto ossia ZL= 0 si ha che l´impedenza è puramente reattiva ed ha la andamento della tangente mentre nel caso il carico sia un circuito aperto l´impedenza è ancora puramente reattiva ma la andamento è quello della cotangente. Infine se ZL = ZC allora Zin = ZC per ogni l ossia la linea è adattata.
8) Coefficiente di riflessione lungo una linea senza perdite :
![]()
ossia il modulo del coefficiente di riflessione è costante lungo la linea mentre varia la sua fase.
9) VSWR :
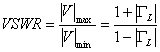
Carta di Smith
10) Mappatura del piano Z nel piano G :
Si basa sulla relazione ![]() da cui per inversione si ottiene
da cui per inversione si ottiene ![]() i punti ad R costante vengono mappati in circonferenze che nel caso di R>0 sono comprese nel cerchio a modulo unitario che si denomina Carta di Smith e passano tutte per il punto GR = 1 . I punti a reattanza costante vengono invece mappati in circonferenze anche esse passanti per il punto GR = 1 ma stavolta esse non intersecano la asse reale, alle reattanze induttive corrispondono cerchi nel semipiano superiore mentre alle reattanze capacitive corrispondono cerchi nel semipiano inferiore. La carta di Smith delle ammettenze si ottiene semplicemente per simmetria della carta di Smith delle impedenze rispetto all´origine, da notare che le ammettenze capacitive sono nel semipiano superiore mentre quelle induttive nel semipiano inferiore mentre i punti del c.a. , c.c. e adattamento rimangono fissi.
i punti ad R costante vengono mappati in circonferenze che nel caso di R>0 sono comprese nel cerchio a modulo unitario che si denomina Carta di Smith e passano tutte per il punto GR = 1 . I punti a reattanza costante vengono invece mappati in circonferenze anche esse passanti per il punto GR = 1 ma stavolta esse non intersecano la asse reale, alle reattanze induttive corrispondono cerchi nel semipiano superiore mentre alle reattanze capacitive corrispondono cerchi nel semipiano inferiore. La carta di Smith delle ammettenze si ottiene semplicemente per simmetria della carta di Smith delle impedenze rispetto all´origine, da notare che le ammettenze capacitive sono nel semipiano superiore mentre quelle induttive nel semipiano inferiore mentre i punti del c.a. , c.c. e adattamento rimangono fissi.
11) Carta di Smith di una linea con e senza perdite :
Dalla ![]() ma considerando distanze positive crescenti avvicinandosi al carico si ha
ma considerando distanze positive crescenti avvicinandosi al carico si ha ![]() che nel caso di linea con perdite diviene
che nel caso di linea con perdite diviene ![]()
Rappresentazione di reti lineari mediante parametri di diffusione
12) Matrice delle ammettenze di corto circuito :
Si ottiene considerando le tensioni come grandezze applicate e le correnti come grandezze risultanti :
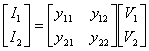
viene detta matrice delle ammettenze in corto circuito in quanto per determinare i parametri y occorre porre una delle due tensioni a zero ossia occorre cortocircuitarla.
13) Matrice delle impedenze a vuoto :
Si ottiene considerando le correnti come grandezze applicate e le tensioni come grandezze risultanti :
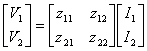
viene detta matrice delle impedenze a vuoto in quanto per determinare i parametri z occorre porre una delle due correnti a zero ossia circuito aperto.
14) Matrice di trasmissione e sue proprietà :
Si ottiene considerando applicate le grandezze alla seconda porta e risultanti le grandezze alla prima porta
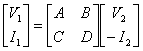
per ricavare i parametri ABCD occorre evidentemente annullare la giusta grandezza alla seconda porta.
È una matrice molto utile in quanto la matrice risultante dalla cascata di reti 2-porte è semplicemente il prodotto delle matrici di trasmissione delle singole porte.
Per una rete simmetrica si ha A = D mentre per una rete reciproca si ha AD-BC=1, infine per un circuito senza perdite A e D sono reali mentre B e C sono immaginari. Una importante proprietà è che la matrice ABCD esiste per ogni rete mentre questo non è vero per le altre tipologie di matrici.
15) Matrice di trasmissione di un tratto di linea senza perdite lunga l ed avente impedenza caratteristica ZC :
Si parte dalle espressioni ![]() e
e ![]() scrivendo l´esponenziale complesso in termini di seno e coseno e sostituendo la condizione di chiusura sul carico ossia
scrivendo l´esponenziale complesso in termini di seno e coseno e sostituendo la condizione di chiusura sul carico ossia ![]() si possono identificare immediatamente i coefficienti della matrice di trasmissione, si ha :
si possono identificare immediatamente i coefficienti della matrice di trasmissione, si ha :
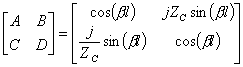
16) Coefficiente di riflessione in termini di onde e matrice di Scattering :
Onda incidente e riflessa possono essere espresse nella forma ![]() e
e ![]() ne segue che il coefficiente di riflessione che è il rapporto tra onda incidente ed onda riflessa assume la forma
ne segue che il coefficiente di riflessione che è il rapporto tra onda incidente ed onda riflessa assume la forma ![]() .
.
Estendendo il concetto ad una rete 2-porte si può introdurre la matrice di dispersione o di scattering
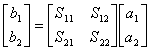
si osservi che per ottenere i parametri di scattering occorrerà annullare l´onda diretta alla porta d´ingresso o a quella d´uscita il che è possibile mediante la adattamento ma questo richiede la conoscenza della impedenza di normalizzazione Z0 . Per una rete reciproca si ha che gli elementi sulla diagonale inversa sono uguali e nel caso di rete passiva evidentemente il modulo di tutti i parametri di scattering è inferiore ad 1 infine nel caso di una rete reciproca e senza perdite si ha che la somma dei quadrati dei parametri di scattering vale 1.
Cavo coassiale
17) Descrizione del cavo coassiale :
È costituito da due conduttori coassiali, uno di raggio ri situato all´interno della altro avente raggio r0. Consente la propagazione di modi TEM e non hanno frequenza di taglio inferiore, la massima frequenza è invece contrassegnata dall´inizio della operatività dei modi TM e TE .
18) Impedenza caratteristica :
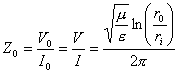
19) Costanti primarie :
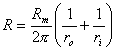 da essa si deduce che tanto più il conduttore interno è piccolo, tanto più sono pesanti le perdite ohmiche., nell´espressione si ha
da essa si deduce che tanto più il conduttore interno è piccolo, tanto più sono pesanti le perdite ohmiche., nell´espressione si ha ![]() che tiene conto delle perdite dei conduttori essendo
che tiene conto delle perdite dei conduttori essendo 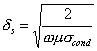 la profondità di penetrazione che diminuisce al crescere della frequenza facendo aumentare le perdite.
la profondità di penetrazione che diminuisce al crescere della frequenza facendo aumentare le perdite.
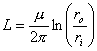 da cui ricordando l´espressione della Z0 si ha che Z0 elevata implica L elevata inoltre è da osservare che è dipendente unicamente dalle caratteristiche geometriche e non della linea e non del dielettrico e del metallo.
da cui ricordando l´espressione della Z0 si ha che Z0 elevata implica L elevata inoltre è da osservare che è dipendente unicamente dalle caratteristiche geometriche e non della linea e non del dielettrico e del metallo.
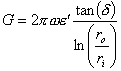 dove
dove ![]() essendo d la angolo di perdita del dielettrico.
essendo d la angolo di perdita del dielettrico.
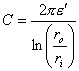 .
.
20) Frequenza massima di utilizzo del cavo coassiale :
È la frequenza oltre la quale intervengono anche modi non TEM, ![]() naturalmente domina ro che quanto più è piccolo tanto più consente al cavo di lavorare ad alta frequenza del resto però al crescere di f abbiamo visto aumentano anche le perdite per via della effetto pelle ed in genere è questa la limitazione che interviene prima.
naturalmente domina ro che quanto più è piccolo tanto più consente al cavo di lavorare ad alta frequenza del resto però al crescere di f abbiamo visto aumentano anche le perdite per via della effetto pelle ed in genere è questa la limitazione che interviene prima.
21) Potenza manipolabile :
È la quantità di potenza RF che il cavo può sopportare soprattutto in termini di temperatura.
22) Massima tensione di utilizzazione :
È la massima differenza di potenziale sopportabile tra il centrale e la calza, non corrisponde alla rigidità dielettrica verso la quale si ha anzi la relazione ![]() , per tensioni superiori si hanno archi nel dielettrico che danno luogo a rumore e danneggiamento del dielettrico.
, per tensioni superiori si hanno archi nel dielettrico che danno luogo a rumore e danneggiamento del dielettrico.
23) Attenuazione :
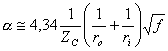 db/100piedi
db/100piedi
24) Isolamento :
Si intende lo schermaggio del campo elettrico interno al cavo rispetto ai campi elettrici esterni, dipende dalla calza la quale può essere a singola maglia, a doppia maglia, a striscia, solida.
Guida d´onda rettangolare
25) Struttura delle guide d´onda :
Si tratta di un conduttore forato a sezione rettangolare caratterizzato da un lato maggiore a e da un lato minore b. Evidentemente prevede una frequenza di taglio inferiore in quanto notoriamente la continua necessita di due conduttori.
26) Frequenza di cut-off :
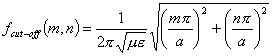
pertanto ad ogni modo avente indici (m,n) è associata una frequenza di cut-off e si propaga soltanto per frequenze superiori ad essa.
27) Modo dominante :
È il modo che possiede la frequenza di cut-off più bassa, in una guida è sempre il TE1,0 mentre per i modi TM il primo modo valido è il TM1,1 il quale possiede una frequenza di cut-off più elevata.
28) Linee di forza di E ed H in una guida d´onda rettangolare :
Il campo elettrico risulta massimo al centro del lato lungo e quindi qui le linee di forza sono più addensate e dirette ortogonalmente a tale lato. Il campo magnetico invece risulta massimo anche esso al centro del lato lungo ma le linee di forza sono parallele a tale lato mentre la componente lungo la direzione di propagazione è nulla al centro del lato lungo.
29) Causa delle perdite nelle guide d´onda :
Le correnti sono distribuite su uno spessore finito del metallo in quanto la conducibilità del metallo non è infinita come dovrebbe essere idealmente, anche il dielettrico poi presenta una conducibilità non nulla ben rappresentabile con una costante dielettrica complessa o con la tangente della angolo di perdita.
30) Banda passante della guida d´onda :
La guida essendo formata da un solo conduttore si comporta come un filtro passa-alto tuttavia si è interessati al comportamento monomodale in quanto i modi presentano tra loro diversa velocità di fase e quindi danno luogo a dispersione nel caso che si consenta che siano operativi più d´uno. Scegliendo a = 2b si fa in modo che il modo TE1,0 sia operativo da solo per una ottava di frequenza. La presenza di perdite del resto porta ad una estensione verso il basso dei modi, ciò in realtà riduce la banda passante della guida in quanto a basse frequenze non si può utilizzare date le forti perdite mentre ad altre frequenze seppure con notevoli perdite si presenta il modo superiore.
31) Caratteristiche salienti delle guide d´onda in uso :
Si hanno due normative, la EIA valida soltanto per le guide e la JAN valida per tutti i mezzi trasmessivi. A bassa frequenza la guida è grossa quindi si preferisce la alluminio che è un conduttore leggero mentre al crescere della frequenza al fine di limitare le perdite vengono utilizzati metalli con una resistività più bassa come l´ottone e la argento.
Vi sono poi guide nelle quali il lato lungo è più del doppio del lato corto, il motivo è da ricercarsi nelle migliori prestazioni nei confronti delle perdite presentate da questa geometria.
Microstriscia
32) Struttura fisica della microstriscia :
Si ha un substrato dielettrico alta h e con costante dielettrica er , al di sotto si ha un piano di massa metallico ed al di sopra una metallizzazione larga W ed alta t. Il substrato può essere sia di tipo “Soft” , come il Duroid che può essere flesso e che a seconda della composizione presenta una ampia variazione della er, che di tipo “Hard” in genere allumina.
33) Approssimazione quasi statica della microstriscia :
Non essendo una struttura omogenea, non consente la propagazione di modi TEM ma soltanto modi “quasi-TEM”. È una struttura difficile da analizzare da un punto di vista elettromagnetico tuttavia l´impedenza caratteristica ![]() può essere determinata immaginando di sostituire il dielettrico con aria essendo C00 la capacità ad unità di lunghezza di tale struttura.
può essere determinata immaginando di sostituire il dielettrico con aria essendo C00 la capacità ad unità di lunghezza di tale struttura.
34) Impedenza caratteristica della microstriscia con dielettrico e suo valore in funzione del rapporto W/h :
Si tratta di espressioni empiriche che una volta fissato il rapporto W/h e la costante dielettrica er consentono di determinare l´impedenza caratteristica della microstriscia, in particolare per microstriscie strette ossia che presentino W/h < 3.3 si ha 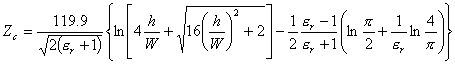 mentre per microstriscie larghe si ha
mentre per microstriscie larghe si ha 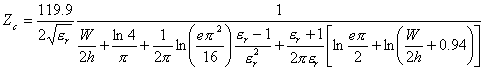
35) Costante dielettrica efficace :
Tiene conto del fatto che la microstriscia è formata da due diversi dielettrici ossia il dielettrico del substrato e la aria, per tener conto di entrambe si ha 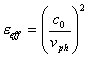 essa è maggiore di er ,ossia il valore che si avrebbe nel caso di una linea molto larga nella quale tutte le linee di forza attraversano il dielettrico, e minore di
essa è maggiore di er ,ossia il valore che si avrebbe nel caso di una linea molto larga nella quale tutte le linee di forza attraversano il dielettrico, e minore di ![]() ossia il valore che si avrebbe nel caso di una linea molto stretta per la quale le linee di forza sono metà in aria e metà nel substrato.
ossia il valore che si avrebbe nel caso di una linea molto stretta per la quale le linee di forza sono metà in aria e metà nel substrato.
36) Fenomeni non considerati nelle espressioni analitiche delle microstriscie :
a) la microstriscia è dispersiva in quanto eeff è funzione della frequenza
b) sia il metallo che il dielettrico presentano delle perdite
c) nelle applicazioni pratiche la struttura va considerata di dimensioni finite ed inscatolata
Discontinuità delle strutture guidanti
37) Discontinuità :
La discontinuità eccita localmente dei modi che in condizioni normali non verrebbero eccitati e che vengono attenuati esponenzialmente allontanandosi dalla discontinuità. Due discontinuità vicine possono inoltre dar luogo a degli zeri di trasmissione.
38) Discontinuità in cavo coassiale :
a) gap capacitivi ossia delle microinterruzioni del centrale che impediscono il passaggio della continua e possono essere anche utilizzate come filtri passa-banda se intervallate da tratti di linea di lunghezza opportuna
b) salti di impedenza si ottengono con una variazione del raggio del conduttore interno e/o di quello esterno
c) finestre capacitive con delle variazioni locali del diametro di uno dei due conduttori
d) giunzioni a T che consentono l´inserimento di Stub in parallelo alla linea
39) Discontinuità in guida d´onda rettangolare :
a) post ossia dei cilindretti metallici che si pongono lungo la sezione trasversale alla direzione di propagazione, si ha un post induttivo se il cilindretto è alto b, un post risonante se è alto L<b oppure un post capacitivo se è alto a ed è posto parallelamente al lato lungo della guida
b) striscie metalliche che possono esser poste parallelamente o ortogonalmente alla direzione di propagazione.
c) diaframmi ossia restringimenti localizzati della guida o nel piano E o nel piano H
d) curvatura (bends) a 90° che possono avvenire sia nel piano E che nel piano H
e) giunzioni a T, unendone due si ottiene il T magico
40) Discontinuità in microstriscia :
a) circuito aperto
b) gap
c) salto di impedenza
d) giunzione a T e a croce
