Divisori ed accoppiatori
1) Geometria del divisore Wilkinson :
Una linea con impedenza caratteristica ZC è connessa tramite un l/4 con impedenza Z2 ad un carico ZL2 e tramite un l/4 con impedenza Z3 ad un carico ZL3 tra queste due linee è poi posta una resistenza R che ha il compito di disaccoppiare. Nel caso in cui l´impedenza di carico sia Z0=50W allora sono necessari due adattatori di impedenza in l/4 . Lo scopo della struttura è di realizzare una partizione di potenza ![]() mentre ovviamente
mentre ovviamente ![]() .
.
2) Equazioni per il progetto del divisore Wilkinson :
a) sostituendo 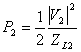 e
e 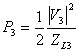 nella
nella ![]() e semplificando tenendo anche presente che affinché non scorra corrente in R occorre che si abbia V1 = V2 si ottiene
e semplificando tenendo anche presente che affinché non scorra corrente in R occorre che si abbia V1 = V2 si ottiene ![]() .
.
b) sostituendo la  nella condizione di adattamento alla porta 1 del divisore
nella condizione di adattamento alla porta 1 del divisore ![]() ed essendo
ed essendo ![]() si ottiene
si ottiene 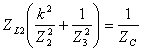 .
.
c) La relazione tra le impedenze dei due tratti di linea a l/4 si ottiene sostituendo nella ![]() le espressioni delle potenze inviate in ingresso alle 2 linee a l/4 in particolare
le espressioni delle potenze inviate in ingresso alle 2 linee a l/4 in particolare 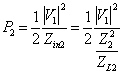 e
e 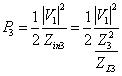 in particolare si ha
in particolare si ha ![]() , una relazione simile a quella tra le impedenze di carico
, una relazione simile a quella tra le impedenze di carico ![]() .
.
d) Il valore della resistenza R deve essere tale che posta in parallelo alla -Y23 dia un´ammettenza equivalente nulla ossia si deve avere ![]() . La Y23 viene calcolata sfruttando una delle equazioni che lega i coefficienti della matrice Y ai coefficienti della matrice ABCD in particolare
. La Y23 viene calcolata sfruttando una delle equazioni che lega i coefficienti della matrice Y ai coefficienti della matrice ABCD in particolare ![]() dove
dove ![]() è quello della matrice ottenuta moltiplicando le matrici ABCD della cascata di una linea lunga l/4 avente impedenza Z2 , una rete con ammettenza Z0 ed una linea lunga l/4 avente impedenza Z3 , sostituendo si ha
è quello della matrice ottenuta moltiplicando le matrici ABCD della cascata di una linea lunga l/4 avente impedenza Z2 , una rete con ammettenza Z0 ed una linea lunga l/4 avente impedenza Z3 , sostituendo si ha ![]() .
.
3) Opzioni progettuali per il divisore Wilkinson :
Essendo di solito ZC = Z0 = 50W , si ha solo un grado di libertà e quindi basta imporre un valore per trovare gli altri :
a) condizione di adattamento a tutte le porte Z2 = ZL2 da cui deriva Z3 = ZL3 , nel caso però in cui si richieda che la potenza venga equamente spartita sulle due porte questa opzione progettuale conduce a Z2 =100W che è molto vicina al valore massimo realizzabile in microstriscia.
b) ![]()
c) ponendo ZL2 = ZL3 = Z0 non ho bisogno dei secondi l/4 che mi adattino verso i carichi Z0 , altrimenti essi sono necessari e le loro impedenze caratteristiche sono ![]() e
e ![]() .
.
4) Divisore Branch-Line :
È una struttura 4 porte costituita da due linee orizzontali separate tramite due linee lunghe ciascuna l/4 e spaziate tra loro di l/4 , essendo doppiamente simmetrica abbiamo che i parametri S da 16 si riducono a 4 e possono essere ricavati immaginando di applicare separatamente alla struttura una alimentazione pari (… si applica alla porta 1 ed alla 4 la stessa tensione ![]() ne deriva che non scorre corrente nelle linee trasversali che possono quindi essere considerate degli stub aperti) ed una alimentazione dispari (… si applica alla porta 1 la tensione
ne deriva che non scorre corrente nelle linee trasversali che possono quindi essere considerate degli stub aperti) ed una alimentazione dispari (… si applica alla porta 1 la tensione ![]() mentre alla porta 4 la tensione
mentre alla porta 4 la tensione ![]() ne deriva le linee trasversali possono essere considerate degli stub in corto).
ne deriva le linee trasversali possono essere considerate degli stub in corto).
5) Parametri S del divisore Branch-Line :
I parametri S della struttura possono essere ricavati in funzione dei parametri S del modello Open Circuit e del modello Short Circuit in particolare sommando i due contributi si ha 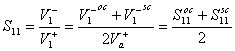 , in maniera analoga si ha
, in maniera analoga si ha ![]() e sfruttando le relazioni di simmetria
e sfruttando le relazioni di simmetria ![]() ,
, ![]() ,
, ![]() ,
, ![]() si ottengono anche
si ottengono anche ![]() e
e ![]() .
.
![]() ed
ed ![]() vengono ricavati a partire dalla matrice di trasmissione che si ottiene dal prodotto delle matrici del primo stub in aperto lungo l/8 , della linea di trasmissione lunga l/4 e del 2° stub in aperto anche esso lungo l/8, si ottiene
vengono ricavati a partire dalla matrice di trasmissione che si ottiene dal prodotto delle matrici del primo stub in aperto lungo l/8 , della linea di trasmissione lunga l/4 e del 2° stub in aperto anche esso lungo l/8, si ottiene 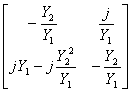 che in virtù delle relazioni tra la matrice S e la matrice ABCD consente di ottenere
che in virtù delle relazioni tra la matrice S e la matrice ABCD consente di ottenere 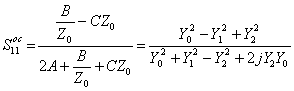 e
e 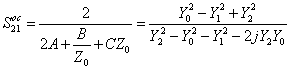 , da queste espressioni si possono ottenere quelle per
, da queste espressioni si possono ottenere quelle per ![]() ed
ed ![]() semplicemente sostituendo Y2 con –Y2 .
semplicemente sostituendo Y2 con –Y2 .
6) Opzioni progettuali del divisore Branch-Line :
La condizione di adattamento alla porta 1 può essere ottenuta uguagliando a zero uno dei due moltiplicandi della 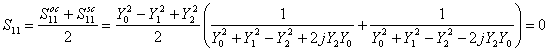 , si hanno i casi :
, si hanno i casi :
a) ![]() da cui segue che S41=0 e quindi la porta 4 è disaccoppiate dalla 1 mentre il segnale alla porta 2 è sfasato di 90° e quello alla porta 3 di 180°. Si può ottenere un divisore a 3dB imponendo |S21|= |S31| che restituisce la condizione
da cui segue che S41=0 e quindi la porta 4 è disaccoppiate dalla 1 mentre il segnale alla porta 2 è sfasato di 90° e quello alla porta 3 di 180°. Si può ottenere un divisore a 3dB imponendo |S21|= |S31| che restituisce la condizione ![]() dove Z1 è l´impedenza dei tratti di linea orizzontali.
dove Z1 è l´impedenza dei tratti di linea orizzontali.
b) ![]() da cui segue che S21=0 e quindi la porta 2 è disaccoppiate dalla 1 mentre il segnale alla porta 3 è sfasato di 180° e quello alla porta 4 di 90°. Si può ottenere un divisore a 3dB imponendo |S31|= |S41| che restituisce la condizione
da cui segue che S21=0 e quindi la porta 2 è disaccoppiate dalla 1 mentre il segnale alla porta 3 è sfasato di 180° e quello alla porta 4 di 90°. Si può ottenere un divisore a 3dB imponendo |S31|= |S41| che restituisce la condizione ![]() dove Z2 è l´impedenza dei tratti di linea verticali.
dove Z2 è l´impedenza dei tratti di linea verticali.
7) Divisore Rat-Race :
È una struttura a 4 porte realizzata in microstriscia nella quale si hanno dei l/4 tra le porte 1 e 2 , 2 e 3 , 3 e 4 mentre si ha un 3l/4 tra la porta 1 e la porta 4, ne consegue che la struttura possiede un solo piano di simmetria verticale e quindi i parametri S necessari a caratterizzarla sono 6 invece che 16. Come nel caso del Branch-Line i parametri S vengono ricavati immaginando di applicare una alimentazione pari (…applicando Va alla porta 1 ed alla porta 4 e Vb alla porta 2 ed alla porta 3 ne deriva che la corrente è nulla sul piano di simmetria e quindi i tratti di linea che ad esso giungono possono essere considerati degli stub aperti) ed una alimentazione dispari (…applicando Va alla porta 1 , –Va alla porta 4 , Vb alla porta 2 e –Vb alla porta 3 ne deriva che la tensione è nulla sul piano di simmetria e quindi i tratti di linea che ad esso giungono possono essere considerati degli stub in corto).
8) Parametri S del divisore Rat-Race :
I parametri S della struttura possono essere ricavati in funzione dei parametri S del modello Open Circuit e del modello Short Circuit in particolare sommando i due contributi si ha 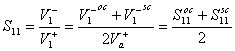 , in maniera analoga si ha
, in maniera analoga si ha ![]() e sfruttando le relazioni di simmetria
e sfruttando le relazioni di simmetria ![]() ,
, ![]() ,
, ![]() ,
, ![]() si ottengono anche
si ottengono anche ![]() e
e ![]() , inoltre in aggiunta rispetto al Branch-Line si hanno
, inoltre in aggiunta rispetto al Branch-Line si hanno ![]() e
e ![]()
![]() ,
, ![]() e
e ![]() vengono ricavati a partire dalla matrice di trasmissione che si ottiene dal prodotto delle matrici del primo stub in aperto, della linea di trasmissione lunga l/4 e del 2° stub in aperto, si ottiene
vengono ricavati a partire dalla matrice di trasmissione che si ottiene dal prodotto delle matrici del primo stub in aperto, della linea di trasmissione lunga l/4 e del 2° stub in aperto, si ottiene 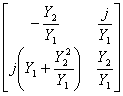 che in virtù delle relazioni tra la matrice S e la matrice ABCD consente di ottenere
che in virtù delle relazioni tra la matrice S e la matrice ABCD consente di ottenere 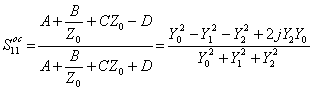 ,
, 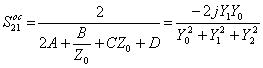 e
e 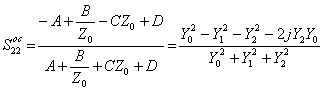 , da queste espressioni si possono ottenere quelle per
, da queste espressioni si possono ottenere quelle per ![]() ,
, ![]() e
e ![]() semplicemente sostituendo Y2 con –Y2 .
semplicemente sostituendo Y2 con –Y2 .
9) Opzioni progettuali del divisore Rat-Race :
La condizione di adattamento alla porta 1 ![]() può essere ottenuta uguagliando a zero
può essere ottenuta uguagliando a zero ![]() , sostituendola insieme alle espressioni trovate per il modello Open Circuit e per il modello Short Circuit nelle espressioni dei parametri di scattering del Rat-Race , abbiamo che il segnale che entra dalla porta 1 esce sfasato di 90° dalla porta 2 e dalla porta 4 mentre non esce dalla porta 3 mentre il segnale in ingresso dalla porta 3 arriva sfasato di 90° alla porta 2.
, sostituendola insieme alle espressioni trovate per il modello Open Circuit e per il modello Short Circuit nelle espressioni dei parametri di scattering del Rat-Race , abbiamo che il segnale che entra dalla porta 1 esce sfasato di 90° dalla porta 2 e dalla porta 4 mentre non esce dalla porta 3 mentre il segnale in ingresso dalla porta 3 arriva sfasato di 90° alla porta 2.
Per ottenere un divisore a 3dB occorre imporre |S21| = |S41|, si ottiene![]() .
.
