Filtri attivi RC con un solo amplificatore
1) Confronto tra i filtri attivi ed i filtri passivi :
I filtri attivi sono più leggeri e richiedono meno spazio rispetto ai filtri passivi, inoltre possono essere realizzati in forma integrata il che ne consente la produzione in massa e la riduzione dei costi.
2) Filosofie di realizzazione dei filtri attivi :
Cascata la funzione di rete è fattorizzata in prodotti di termini del 2° ordine ognuno dei quali è realizzato individualmente da un circuito RC attivo e posto in cascata agli altri.
Diretta la funzione di rete viene realizzata completamente da un unico circuito
3) VCVS :
È una sorgente di tensione controllata in tensione, idealmente ha le seguenti caratteristiche :
a) impedenza d´ingresso infinita
b) impedenza d´uscita nulla
c) tensione d´uscita linearmente proporzionale tramite un guadagno alla tensione d´ingresso
Nei VCVS realizzati con amplificatori operazionali l´impedenza d´ingresso è di qualche MW mentre l´impedenza d´uscita è minore di 100W .
4) Configurazioni per un amplificatore operazionale utilizzato come VCVS :
Invertente il segnale è applicato tramite la resistenza R1 al morsetto invertente al quale giunge anche il segnale d´uscita tramite la resistenza R2 , il morsetto positivo è a massa e quindi il guadagno risulta essere ![]() .
.
Non Invertente il segnale è applicato al morsetto positivo mentre al morsetto negativo è collegata verso massa la resistenza R1 e la resistenza di retroazione R2 , il guadagno risulta essere ![]() .
.
Inseguitore è un amplificatore non invertente in cui R2 = 0 il che implica K=1 ossia V2 = V1 .
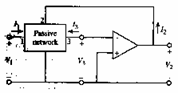
5) Filtro generale a singolo amplificatore :
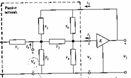
 La rete passiva in figura è caratterizzata dalle equazioni
La rete passiva in figura è caratterizzata dalle equazioni 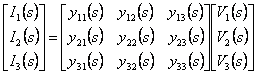 nelle quali per la presenza del VCVS si può sostituire
nelle quali per la presenza del VCVS si può sostituire ![]() ed eliminare la 2ª equazione in quanto Zout=0 , essendo inoltre I3 = 0 si ottiene
ed eliminare la 2ª equazione in quanto Zout=0 , essendo inoltre I3 = 0 si ottiene ![]() che per la realizzazione
che per la realizzazione
implica ![]() ,
, ![]() ,
, ![]() .
.
6) Sallen & Key passa-basso :
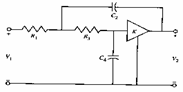 Dalla uguaglianza
Dalla uguaglianza 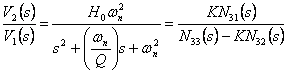 e ricordando i valori trovati per N31 , N32 , N33 si osserva che Y1 ed Y3 debbono essere costanti ossia conduttanze Y1 = G1 e Y3 = G3 inoltre N32 deve avere uno zero semplice nell´origine quindi Y2=sC2 ed Y6=0 mentre N33 deve essere del 2° ordine con zeri reali negativi e quindi si ottiene Y4 =sC4 ed Y5=0 , ne segue che
e ricordando i valori trovati per N31 , N32 , N33 si osserva che Y1 ed Y3 debbono essere costanti ossia conduttanze Y1 = G1 e Y3 = G3 inoltre N32 deve avere uno zero semplice nell´origine quindi Y2=sC2 ed Y6=0 mentre N33 deve essere del 2° ordine con zeri reali negativi e quindi si ottiene Y4 =sC4 ed Y5=0 , ne segue che 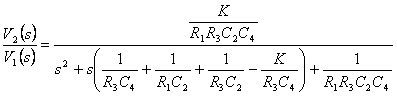
Per tale schema alcuni criteri di progetto sono i seguenti :
a) sia R1 = R3= R ed anche C2 = C4 = C si ottiene ![]() ,
, ![]() ,
, ![]()
b) sia K=1 , ![]() ,
, ![]() , R1 = R e C2 = C , si ottiene
, R1 = R e C2 = C , si ottiene ![]() ed
ed ![]()
c) sia K=2 , C2 = C4 = C , si ottiene ![]() ed
ed ![]()
Tutti e 3 i progetti danno luogo a sensibilità direttamente proporzionali a Q il che è deleterio quando si vogliano realizzare filtri a Q elevato meglio ottenibili utilizzando rapporti 1:10 invece che 1:1 tra R1 ed R3 o tra C2 e C4 .
7) Sallen & Key passa-banda :
Dalla uguaglianza  e ricordando i valori trovati per N31 , N32 , N33 si osserva che Y1 ed Y3 debbono essere uno un condensatore e la altro un resistore, assumiamo Y1 = G1 e Y3 = sC3 per soddisfare la condizione su N32 si deve avere Y2=G2 ed Y6=0 mentre per soddisfare quella su N33 poniamo Y4 =G4 ed Y5=sC5 , si ottiene
e ricordando i valori trovati per N31 , N32 , N33 si osserva che Y1 ed Y3 debbono essere uno un condensatore e la altro un resistore, assumiamo Y1 = G1 e Y3 = sC3 per soddisfare la condizione su N32 si deve avere Y2=G2 ed Y6=0 mentre per soddisfare quella su N33 poniamo Y4 =G4 ed Y5=sC5 , si ottiene  .
.
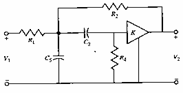
Per tale schema alcuni criteri di progetto sono i seguenti :
a) sia R1 = R2 = R4 = R ed anche C3 = C5 = C si ottiene ![]() e
e ![]()
b) sia K=2 e R1= C3 = C5 =1 si ottiene 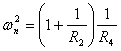 ed
ed ![]()
8) Sallen & Key passa-alto :
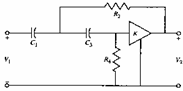 Dalla uguaglianza
Dalla uguaglianza 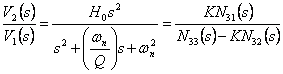 e ricordando i valori trovati per N31 , N32 , N33 si trova che deve essere Y1=sC1 , Y2=G2 , Y3 = sC3 , Y4=G4 , Y5 = Y6 = 0 , si ottiene
e ricordando i valori trovati per N31 , N32 , N33 si trova che deve essere Y1=sC1 , Y2=G2 , Y3 = sC3 , Y4=G4 , Y5 = Y6 = 0 , si ottiene 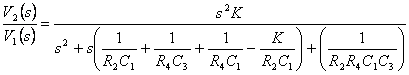
Per tale schema alcuni criteri di progetto sono i seguenti :
a) sia R2 = R4 = R e C1 = C3 = C si ottiene ![]() ,
, ![]() ,
, ![]() .
.
b) sia K=1 , ![]() ,
, ![]() , C1=C , R2=R si ottiene
, C1=C , R2=R si ottiene ![]() e
e ![]()
c) sia K=2 e C1 = C3 = C , si ottiene ![]() e
e 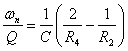
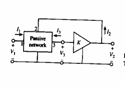
9) Filtro generale a guadagno infinito con singolo amplificatore :
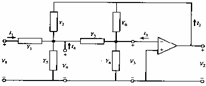 La rete passiva in figura è caratterizzata dalle equazioni
La rete passiva in figura è caratterizzata dalle equazioni 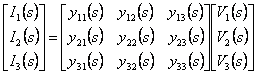 nelle quali per la presenza della amplificatore operazionalesi ha V3 = 0 , si può eliminare la 2ª equazione in quanto Zout=0 , essendo inoltre I3 = 0 si ottiene
nelle quali per la presenza della amplificatore operazionalesi ha V3 = 0 , si può eliminare la 2ª equazione in quanto Zout=0 , essendo inoltre I3 = 0 si ottiene ![]() che per la realizzazione
che per la realizzazione
in figura si riduce a ![]() .
.
10) Infinite-gain passa-basso :
Dalla uguaglianza 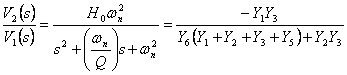 si deduce che per quanto riguarda i denominatori deve essere Y1 = G1 e Y3 = G3 mentre per i denominatori Y2 = G2 , Y5 = sC5 , Y6 = sC6 si giunge pertanto alle equazioni
si deduce che per quanto riguarda i denominatori deve essere Y1 = G1 e Y3 = G3 mentre per i denominatori Y2 = G2 , Y5 = sC5 , Y6 = sC6 si giunge pertanto alle equazioni ![]() ,
, 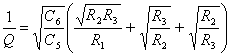 ,
, ![]() .
.

Un criterio di progetto consiste nel porre C5 = C e C6 = mC con ![]() , si ottiene
, si ottiene ![]() ,
, ![]() ,
, ![]() .
.
Si tratta di un filtro ideale per le realizzazioni a Q elevato in quanto presenta una sensibilità di Q rispetto alle variazioni dei parametri sempre inferiore ad 1 .
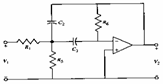
11) Infinite-gain passa-banda :
Dalla uguaglianza  si ha che ponendo Y1=G1 , Y3 =sC3 , Y2=sC2 , Y5=G5 e Y6=G6
si ha che ponendo Y1=G1 , Y3 =sC3 , Y2=sC2 , Y5=G5 e Y6=G6
Un possibile criterio di progetto consiste nel porre C2=C3=C , si ottiene ![]() ,
, ![]() ,
, ![]() .
.
12) Infinite-gain passa-alto :
Dalla uguaglianza 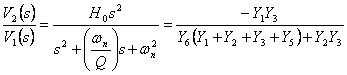 si ha che ponendo Y1=sC1 ,
si ha che ponendo Y1=sC1 ,
Y2 =sC2 , Y3=sC3 , Y5=G5 e Y6=G6
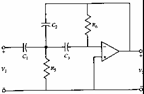
Un possibile criterio di progetto consiste nel porre C1 = C3 = C , si ottiene :
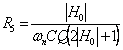 ,
, ![]() ,
, ![]() ..
..
13) Criteri di progetto per filtri in cascata di ordine maggiore di 2 :
Se si deve realizzare un filtro con ordine dispari la sezione del 1° ordine costituita da un RC o CR va posta all´inizio della cascata e seguita da un inseguitore di tensione, le restanti sezioni del 2° ordine vanno ordinate con Q crescente.
