Metodi per la realizzazione diretta
1) Equazioni che descrivono i parametri di trasmissione :
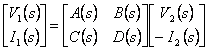
2) GIC :
(Generalized Impedance Converter )
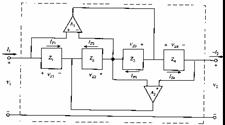
Si tratta di un circuito che consente di realizzare mediante componenti attivi RC diversi tipi di componenti passivi , alcuni dei quali originali. Il circuito è il seguente :
Sfruttando il fatto che la differenza di potenziale ai morsetti d´ingresso della operazionale è 0 e che dagli stessi non assorbe corrente , si ottiene la matrice di trasmissione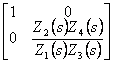 
.
3) GIN e sua impedenza di ingresso :
(Generalized Impedance Network)
Si ottiene terminando il GIC con una impedenza Z5(s) , si ottiene una impedenza d´ingresso 
che espressa in termini di ammettenza è 
. Mediante opportuna scelta delle impedenze si possono simulare sia induttanze che nuovi componenti passivi.
4) Realizzazione di induttanze mediante GIN :
Si utilizza una GIN in cui tutte le impedenze sono delle resistenze tranne Z4 che è una capacità, ne segue che l´impedenza d´ingresso è di tipo induttivo 
, utilizzando amplificatori operazionali di tipo matched gli effetti dei loro parametri non ideali vengono minimizzati tuttavia l´induttanza realizzata utilizza componenti attivi e pertanto necessita di una connessione verso massa il che ne consente l´utilizzo soltanto nei filtri passa-alto dove le induttanze sono poste trasversalmente. Le sensibilità agli elementi del GIN sono ±1 volta le sensibilità all´induttore simulato.
5) FDNR :
È un elemento che presenta una ammettenza d´ingresso 
dove D è una costante reale positiva che si misura in Farad-secondo . Il motivo del nome si ottiene sostituendo s = jw , si ha infatti Y(jw) = -w2D quindi un´ammettenza negativa e dipendente dalla frequenza. Ricordando che la ammettenza d´ingresso del GIN è 
si può realizzare un FDNR scegliendo Y1 ed Y5 come ammettenze di condensatori e le restanti ammettenze sono conduttanze, si ottiene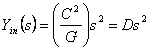 
. Gli FDNR possono essere utilizzati soltanto nella realizzazione di filtri passa-basso e passa-banda infatti applicando la trasformazione di Bruton RLC « CRD consistente in una denormalizzazione d´impedenza con 
si ha che le induttanze serie vengono trasformate in conduttanze ed i condensatori shunt in FDNR. Inoltre per consentire un percorso verso massa alla continua, i condensatori vengono bypassati da opportune resistenze. La realizzazione dei passa-banda con FDNR è più complessa in quanto è meglio non siano flottanti, si ovvia al problema utilizzando la cascata di un GIC , un GIN con impedenza Z(s) = s2D ed un altro GIC.
6) Leapfrog :
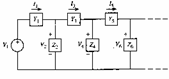La tecnica Leapfrog non si occupa di simulare il comportamento di alcuni elementi passivi bensì simula mediante delle tensioni sia le correnti serie che le tensioni shunt di una rete a scala passiva
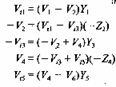Alla quale possiamo associare le equazioni e quindi il diagramma a blocchi
 |
Pertanto a partire da una rete RLC semplicemente o doppiamente caricata ottenuta tramite le tabelle si individuano i diversi blocchi e li si realizza mediante integratori sia semplici che con perdite , invertitori e sommatori.
Nel caso si desideri realizzare un passa-banda , i blocchi da simulare sono di tipo RLC oppure LC quindi possono essere realizzati con uno qualsiasi dei circuiti che realizzano funzioni del 2° ordine , il più adatto è il Tow-Thomas in quanto l´uscita passa-banda è disponibile sia invertente che non. In ogni caso si ottengono delle sensibilità prossime a quelle del circuito passivo di partenza.
7) Filtri a capacità commutata :
Nei circuiti integrati le resistenze di valore elevato occupano molto spazio , esse possono essere realizzate in molto meno spazio e con più precisione utilizzando una capacità commutata secondo il seguente schema
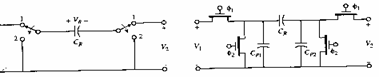
Per la quale con j1 alto e j2 basso si ha
mentre con j2 alto e j1 basso Q2 = 0 quindi 
Þ 
Þ 
.
SI può ottenere un resistore negativo utilizzando una diversa configurazione delle fasi del clock
Si ha infatti 
.
Le resistenze così realizzate possono essere utilizzate per realizzare integratori invertenti, non invertenti e con perdite nonché filtri Tow-Thomas e Leapfrog , si deve in ogni caso utilizzare una frequenza di clock almeno doppia rispetto alla massima frequenza presente nel segnale d´ingresso , in ottemperanza al criterio di Nyquist, nella pratica essa è almeno 100 volte maggiore. L´utilizzo dei 4 MOSFET consente inoltre di minimizzare l´effetto delle capacità parassite degli stessi quando si vogliano utilizzare condensatori della ordine del pF col fine di risparmiare spazio nel circuito integrato.