Approssimazione
1) Proprietà della |N(jw)|2 associata ad una funzione razionale N(s) :
a) |N(jw)|2 è un rapporto di polinomi pari in w ciò si ottiene sostituendo jw = s nella ![]() ed utilizzando
ed utilizzando ![]()
b) sostituendo ![]() nella |N(jw)|2 si ottiene la
nella |N(jw)|2 si ottiene la ![]() dove N(-s) ha gli stessi poli di N(s) ma riflessi rispetto all´origine , ne deriva che i poli di T(s2) hanno simmetria quadrantale ossia sono simmetrici sia rispetto alla asse reale che rispetto alla asse immaginario . Tale simmetria quadrantale è possibile solo se i poli e zeri presenti sulla asse jw sono di ordine pari.
dove N(-s) ha gli stessi poli di N(s) ma riflessi rispetto all´origine , ne deriva che i poli di T(s2) hanno simmetria quadrantale ossia sono simmetrici sia rispetto alla asse reale che rispetto alla asse immaginario . Tale simmetria quadrantale è possibile solo se i poli e zeri presenti sulla asse jw sono di ordine pari.
2) Funzione massimamente piatta :
È una funzione |N(jw)|2 che è massimamente piatta a ridosso della origine, ricordando che |N(jw)|2 è un rapporto di polinomi pari ![]() e confrontando l´ultimo termine ottenuto mediante rapporto con l´espansione in serie di Mac Laurin
e confrontando l´ultimo termine ottenuto mediante rapporto con l´espansione in serie di Mac Laurin ![]() che per essere massimamente piatta deve avere il maggiore numero di derivate nulle nell´origine , ne deriva che |N(jw)|2 massimamente piatta si può ottenere se ai = bi per il maggior numero di coefficienti possibile.
che per essere massimamente piatta deve avere il maggiore numero di derivate nulle nell´origine , ne deriva che |N(jw)|2 massimamente piatta si può ottenere se ai = bi per il maggior numero di coefficienti possibile.
3) Funzione di Butterworth :
Ci si propone di realizzare una |N(jw)|2 massimamente piatta quindi ai = bi , di tipo passa-basso quindi tutti gli zeri di trasmissione sono ad infinito e quindi tutti i bi sono zero come pure quindi gli ai tranne quello di grado massimo , si ha :
![]()
dove al denominatore c´è w2n in quanto |N(jw)|2 deve essere un rapporto di polinomi pari. La posizione dei poli si ottiene sostituendo jw=s cioè w2= -s2 nella |N(jw)|2 , si ha ![]() , in particolare :
, in particolare :
a) per n dispari ![]() con k = 1 , 3 , 5 , 4n-1
con k = 1 , 3 , 5 , 4n-1
b) per n pari ![]() con k = 0 , 2 , 4 , 4n-2
con k = 0 , 2 , 4 , 4n-2
soltanto i poli che si trovano nel semipiano sinistro sono stabili, essi sono ![]() con
con ![]() e
e ![]() .
.
4) Polinomio di Butterworth :
È il polinomio che si trova a denominatore della funzione di Butterworth ![]() dove a0 = 1 dato che tutti i poli si trovano sul cerchio unitario e gli altri coefficienti si ricavano ricorsivamente mediante la
dove a0 = 1 dato che tutti i poli si trovano sul cerchio unitario e gli altri coefficienti si ricavano ricorsivamente mediante la  e sono simmetrici ossia a0 = an , a1 = an-1 , … .
e sono simmetrici ossia a0 = an , a1 = an-1 , … .
5) Determinazione della ordine di una funzione di Butterworth :
L´ordine nB di una funzione di Butterworth è ![]() dove
dove ![]() ed
ed  essendo nelle specifiche che la banda passante deve essere compresa tra 0 ed wp e presentare una deviazione massima di Kp dB rispetto al valore massimo mentre la stop band è compresa tra ws ed ¥ e presenta una attenuazione minima di Ks dB .
essendo nelle specifiche che la banda passante deve essere compresa tra 0 ed wp e presentare una deviazione massima di Kp dB rispetto al valore massimo mentre la stop band è compresa tra ws ed ¥ e presenta una attenuazione minima di Ks dB .
6) Denormalizzazione di frequenza :
La funzione di Butterworth normalizzata prevede una frequenza di taglio ad 1 rad/sec per la quale Kp è 3dB, per avere una diversa attenuazione alla stessa frequenza, occorre effettuare la denormalizzazione di frequenza ![]() essendo
essendo ![]() la pulsazione alla quale la funzione ha la desiderata attenuazione Kp .
la pulsazione alla quale la funzione ha la desiderata attenuazione Kp .
7) Polinomi di Chebyshev :
![]()
dove i polinomi Cn(w) sono definiti mediante una delle seguenti :
a) ![]() a partire da C1(w) = w
a partire da C1(w) = w
b) ![]()
c) ![]()
d) ![]()
sono tali che il modulo è equi-ripple in banda passante e monotonico decrescente in banda oscura. Le pulsazioni w cui corrisponde una attenuazione di –3dB alla pulsazione di 1rad/s sono date dalla relazione ![]() .
.
I poli si ricavano sostituendo ![]() nella |N(jw)|2 , essi sono situati su di una ellisse centrata nell´origine.
nella |N(jw)|2 , essi sono situati su di una ellisse centrata nell´origine.
8) Determinazione della ordine di una funzione di Chebyshev :
L´ordine nC di una funzione di Chebyshev è ![]() dove
dove ![]() ed
ed  essendo nelle specifiche che la banda passante deve essere compresa tra 0 ed wp e presentare una deviazione massima di Kp dB rispetto al valore massimo mentre la stop band è compresa tra ws ed ¥ e presenta una attenuazione minima di Ks dB .
essendo nelle specifiche che la banda passante deve essere compresa tra 0 ed wp e presentare una deviazione massima di Kp dB rispetto al valore massimo mentre la stop band è compresa tra ws ed ¥ e presenta una attenuazione minima di Ks dB .
9) Funzione di Chebyshev inversa :

essa presenta una caratteristica equi-ripple nella banda oscura e monotonica decrescente nella banda passante.
Si ottiene sostituendo w con 1/w nella ![]() che è equi-ripple lontano dall´origine ma passa-alto. I poli che ne risultano sono reciproci rispetto a quelli trovati per
che è equi-ripple lontano dall´origine ma passa-alto. I poli che ne risultano sono reciproci rispetto a quelli trovati per ![]() .
.
10) Determinazione della ordine della funzione di Chebyshev inversa :
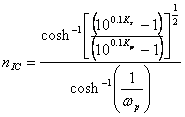
confrontando questa espressione con quella trovata per il filtro di Chebyshev si ha che sono uguali a patto che si abbia
![]()
![]()
![]()
11) Filtri ellittici :
Sono anche detti filtri di Cauer e presentano una caratteristica equi-ripple sia in banda oscura che in banda passante inoltre sono caratterizzati da una pendenza maggiore in corrispondenza della frequenza di taglio rispetto alle altre tipologie di filtri. La forma tipica di un filtro ellittico è ![]() dove
dove  .
.
12) Trasformazione da passa-basso a passa-alto :
Se una funzione passa-basso è definita nel piano complesso s = s + jw mediante la trasformazione ![]() si ottiene una funzione passa-alto nel piano p = u + jv , imponendo lo stato stazionario sinusoidale s = 0 si ottiene u = 0 ,
si ottiene una funzione passa-alto nel piano p = u + jv , imponendo lo stato stazionario sinusoidale s = 0 si ottiene u = 0 , ![]() . L´effetto sulla funzione di rete N(s) è che gli zeri di trasmissione all´infinito vengono trasformati in zeri nell´origine. La trasformazione può anche essere applicata direttamente agli elementi di una rete , cosicchè un induttore di K Henry si trasforma in un condensatore di
. L´effetto sulla funzione di rete N(s) è che gli zeri di trasmissione all´infinito vengono trasformati in zeri nell´origine. La trasformazione può anche essere applicata direttamente agli elementi di una rete , cosicchè un induttore di K Henry si trasforma in un condensatore di ![]() Farad mentre un condensatore di K Farad si trasforma in un induttore di
Farad mentre un condensatore di K Farad si trasforma in un induttore di ![]() Henry.
Henry.
13) Trasformazione da passa-basso a passa-banda :
Se una funzione passa-basso è definita nel piano complesso s = s + jw mediante la trasformazione ![]() si ottiene una funzione passa-banda nel piano p = u + jv , imponendo lo stato stazionario sinusoidale s = 0 si ottiene u = 0 ,
si ottiene una funzione passa-banda nel piano p = u + jv , imponendo lo stato stazionario sinusoidale s = 0 si ottiene u = 0 , 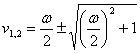 . In particolare la banda del passa-basso diviene la banda del passa-banda ed ogni coppia (v1,v2) è tale che v1v2=1 . La trasformazione può anche essere applicata direttamente agli elementi di una rete mettendo in serie ad ogni induttore di K Henry una capacità di
. In particolare la banda del passa-basso diviene la banda del passa-banda ed ogni coppia (v1,v2) è tale che v1v2=1 . La trasformazione può anche essere applicata direttamente agli elementi di una rete mettendo in serie ad ogni induttore di K Henry una capacità di ![]() Farad ed in parallelo ad ogni capacità di K Farad un induttore di
Farad ed in parallelo ad ogni capacità di K Farad un induttore di ![]() Henry .
Henry .
14) Realizzazione di un filtro passa-banda di tipo Broad-Band :
È un filtro passa-banda con una larghezza di banda maggiore rispetto al filtro normalizzato, si ottiene operando una denormalizzazione in frequenza sul filtro passa-basso e poi eseguendo la trasformazione passa-basso® passa-banda .
15) Realizzazione di un filtro elimina-banda :
Occorre applicare la trasformazione ![]() ad un filtro passa-alto
ad un filtro passa-alto
16) Approssimazione di banda stretta :
Un filtro passa-banda è detto essere a banda stretta se la sua larghezza di banda è minore di un decimo rispetto alla frequenza di centro banda ossia se ![]() . Il denominatore della funzione passa-banda si può ottenere direttamente in forma fattorizzata infatti sostituendo
. Il denominatore della funzione passa-banda si può ottenere direttamente in forma fattorizzata infatti sostituendo ![]() nella
nella ![]() si ottiene
si ottiene ![]() dove s è la variabile rispetto alla quale è definito il passa-basso mentre p è la variabile rispetto alla quale è definito il passa-banda.
dove s è la variabile rispetto alla quale è definito il passa-basso mentre p è la variabile rispetto alla quale è definito il passa-banda.
