La trasformata di Fourier discreta
1) Rappresentazione in serie di Fourier discreta di una sequenza periodica :
La formula di sintesi è  mentre la formula di analisi è
mentre la formula di analisi è 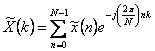 .
.
Definendo ![]() esse possono esser scritte
esse possono esser scritte ![]() e
e ![]() .
.
Si osservi che i valori ![]() nella rappresentazione mediante la DFS di una sequenza periodica, coincidono con i valori della trasformata z di un singolo periodo di
nella rappresentazione mediante la DFS di una sequenza periodica, coincidono con i valori della trasformata z di un singolo periodo di ![]() presi in N punti spaziati uniformemente sul circolo unitario.
presi in N punti spaziati uniformemente sul circolo unitario.
2) Proprietà della serie di Fourier discreta :
 |
3) Relazione tra una sequenza aperiodica x(n) avente trasformata X(z) e la sequenza periodica i cui coefficienti della DFS coincidono con i campioni di X(z) equispaziati in angolo sul circolo unitario :
![]()
ossia la sequenza periodica si ottiene dalla sequenza aperiodica sovrapponendo ripetizioni successive di quest´ultima, ciò comporta che se la sequenza aperiodica x(n) è di durata finita inferiore ad N allora non c´è aliasing.
4) Possibili punti di vista per la trasformata di Fourier di sequenze a durata finita :
a) si associa alla sequenza di durata finita lunga N una sequenza periodica di periodo N avente rappresentazione unica mediante la DFS.
b) La sequenza periodica ottenuta campionando la trasformata Z in N punti equispaziati sul circolo unitario è identica ai coefficienti della DFS.
5) Sequenza rettangolo :
![]()
6) Trasformata di Fourier discreta :
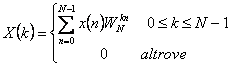

7) Proprietà della trasformata di Fourier discreta :

8) Esecuzione della traslazione circolare di una sequenza :
Da una sequenza x(n) si può ottenere una sequenza periodica ![]() se su questa si esegue una traslazione di m campioni, la sequenza che si ottiene è diversa da quella che si ottiene semplicemente traslando la sequenza x(n), si immagini infatti di prendere un periodo della sequenza, chiuderlo come a formare un cilindro, ruotarlo di n passi e poi riaprirlo.
se su questa si esegue una traslazione di m campioni, la sequenza che si ottiene è diversa da quella che si ottiene semplicemente traslando la sequenza x(n), si immagini infatti di prendere un periodo della sequenza, chiuderlo come a formare un cilindro, ruotarlo di n passi e poi riaprirlo.
9) Esecuzione della convoluzione circolare :
La convoluzione lineare consiste nel prendere una delle due sequenze, ribaltarla e traslarla e campione per campione sommare i prodotti, nella convoluzione circolare invece si deve immaginare di prendere un solo periodo di entrambe le sequenze e formare due cilindri concentrici, far ruotare uno rispetto alla altro e sommare i prodotti. Si osservi che questa operazione corrisponde a moltiplicare le trasformate di Fourier discrete di due sequenze, il risultato antitrasformato restituisce la convoluzione delle due sequenze.
10) Calcolo della convoluzione lineare basato sulla trasformata di Fourier discreta :
![]()
9) Metodi di calcolo della convoluzione di una sequenza di durata finita (filtro) con una sequenza di durata infinita : Sovrapposizione e somma
la sequenza infinita viene suddivisa in sequenze di durata L aventi aggiunti degli zeri in modo tale che sommando le infinite sequenze ottenute si riottiene la sequenza infinita iniziale. Eseguendo la convoluzione circolare di ciascuna di queste sequenze con la sequenza del filtro, si ottengono delle sequenze formate da L+M-1 campioni dei quali M-1 si sovrappongono, quindi sommando i segmenti filtrati si ottiene il segnale filtrato.
Sovrapposizione ed estrazione
la sequenza infinita viene suddivisa in sequenze sovrapponibili di lunghezza N, si calcolano le convoluzioni circolari dopodiché si elimina una parte da ciascuna di esse ed i risultati si giuntano.
