Ricezione in presenza di rumore
Ricezione numerica in presenza di rumore
1) Caratteristiche della ricezione numerica in presenza di rumore :
Supponiamo che un canale numerico reale sia affetto da AWGN , esso può essere rappresentato su una base di ¥ versori che contenga la base ad n versori sulla quale è rappresentato il processo utile. Il rumore nr(t) rappresentato sui primi N versori contiene informazioni sul processo mentre nI(t) rappresentato sui restanti ¥ - N versori è indipendente sia dal processo utile che da nr(t) , viene chiamato rumore irrilevante e trascurato nella restante trattazione. Il rumore è rappresentato quindi nello spazio dei segnali dal vettore 
dove le nj hanno densità di probabilità del 1° ordine 
, analogamente il segnale ricevuto rr(t) è descritto dal vettore osservabile 
con 
che sono v.a. continue in quanto somma di una v.a. discreta ed una v.a. continua .
2) Demodulazione e decisione in presenza di rumore :
Si suppone che la modulazione numerica sia stata priva di codifica e utilizzante una trasformazione serie-parallelo, essa abbia associato ad ogni elemento della costellazione una parola binaria con 
bit . Lo schema del demodulatore numerico è :
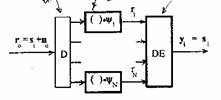all´uscita del banco di correlatori si hanno le componenti rj del vettore osservabile r0 che per via del rumore non coincide con nessun vettore della costellazione , si ha infatti che la probabilità di ricevere rj una volta che sia stato emesso sd è 
ed essendo le nj statisticamente indipendenti si ha 
.
È pertanto necessario un decisore il quale applicando un criterio di decisione associa r0 ad uno dei vettori della costellazione.
3) Criteri di decisione :
CRITERIO MAP (Maximum A Posteriori probability)
 |
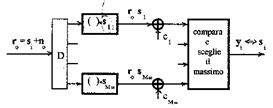Per ogni vettore sd che può essere emesso dal modulatore si calcola la probabilità condizionata
dopodichè si sceglie il vettore sj se 
per ogni i ¹ j , ne risulta che la probabilità di errata decisione è minima e quindi il criterio è ottimo. Le in genere non sono note mentre invece lo sono le 
allora applicando il teorema di Bayes si ha 
quindi osservando che il solo numeratore è funzione di i si ottiene una formulazione alternativa del criterio MAP secondo la quale si sceglie sj se 
per ogni i ¹ j . Ricordando poi che 
si perviene alla 3ª formulazione del criterio MAP secondo la quale si sceglie sj se 
per ogni i ¹j che in sostanza implica la suddivisione dello spazio dei segnali in regioni di decisione pesate con la probabilità di emissione di ogni vettore della costellazione. Da quest´ultima formulazione del Criterio MAP si evince che esso è verificato se si ha il massimo della funzione vettoriale 
con 
pertanto si ha il seguente schema alternativo di demodulatore numerico con decisore .
CRITERIO ML (Maximum Likelihood = Massima verosimiglianza)
È un criterio subottimo secondo il quale si sceglie sj se 
per ogni i ¹ j cui banalmente corrisponde la formulazione alternativa secondo la quale si sceglie sj se 
per ogni i ¹j ossia si sceglie il vettore sj della costellazione che risulta essere il più vicino ad r0 . In questo caso essendo assenti le probabilità di emissione dei singoli vettori, le regioni di decisione hanno tutte la medesima area.
4) Probabilità di corretta e di errata decisione :
Ricordando che i criteri di decisione non fanno altro che associare ad ogni vettore della costellazione una regione di decisione, ne segue che la probabilità di corretta decisione condizionata al vettore emesso sd è l´integrale di 
sulla regione Dd associata ad sd , si ha cioè 
mentre la probabilità di corretta decisione è 
e la probabilità di errore PE = 1-PC . Infine la probabilità di errore Pe è la probabilità che vi sia un bit errato ed è funzione della codifica di modulazione utilizzata, ad esempio nel caso di modulazione antipodale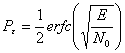 
.
Stima lineare di segnale continuo
5) Caratteristiche della stima continua :
Il processo ricevuto 
è la somma di un processo utile stazionario o ciclostazionario con realizzazione continua s(t) a valor medio nullo e densità spettrale P(f) nota cui corrisponde una potenza P(f) , e di un rumore additivo gaussiano con realizzazione n(t) a valor medio statistico nullo e densità spettrale N(f) , a partire da r(t) lo stimatore fornisce una stima continua lineare 
della sola parte utile s(t) compresa in r(t) , l´errore di stima commesso è 
. Per un dato istante t0 le prestazioni dello stimatore sono funzione di s(t) = s e vengono caratterizzate tramite la polarizzazione condizionata 
, la varianza condizionata della errore 
e l´errore quadratico medio condizionato 
i cui valori attesi sono rispettivamente la polarizzazione 
, la varianza della errore 
e l´errore quadratico medio 
. Si ha inoltre un indicatore relativo adimensionale chiamato qualità della stima continua 
che in sostanza è un rapporto segnale-rumore .
6) Caratteristiche degli stimatori LTI :
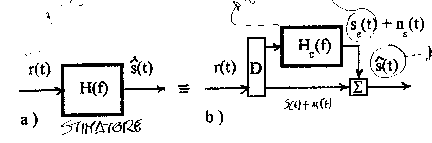Lo stimatore deve necessariamente introdurre distorsione in quanto deve favorire il transito delle componenti spettrali di r(t) per le quali il segnale utile prevale sul rumore e ostacolare invece il transito delle componenti per le quali il rumore prevale sul segnale. Ammettendo la sola distorsione lineare di ampiezza si ha il seguente schema equivalente per lo stimatore che evidenzia come la stima continua sia sia composta da 4 addendi
dove n(t) ed ne(t) sono disturbi mentre se(t) è un disturbo se 
.
Si trova che le caratteristiche dello stimatore sono 
, 
, 
, 
essendo Pe la potenza del disturbo dovuta alla distorsione lineare di ampiezza, 
la potenza del solo rumore in uscita e 
la potenza del processo di stima LTI. Si osservi che l´ottimizzazione della qualità della stima è invariante rispetto alla presenza di un fattore costante nella funzione di trasferimento impiegata, questo risultato viene impiegato per ricondursi sempre al caso particolare di rumore additivo gaussiano bianco mediante uno sbiancatore 
da anteporre allo stimatore ed uno sbiancatore complementare da postporre.
15) Tipologie di stimatori LTI :
Stimatore lineare ottimo di Wiener-Hopf
Minimizzando 
si massimizza la qualità della stima, tale ottimizzazione è effettuata dal filtro di Wiener-Hopf 
con 
, antitrasformando si trova una risposta impulsiva reale e pari quindi anticausale pertanto il quadripolo non è fisicamente realizzabile, si utilizza allora un filtro la cui risposta impulsiva approssimi quella di Wiener-Hopf per t > 0 ma sia nulla per t < 0 .
Stimatore lineare con taglio ottimo di banda
Consideriamo per semplicità un rumore bianco con densità spettrale N0 , lo stimatore lineare con taglio ottimo di banda ha funzione di trasferimento rettangolare che vale gt0 per le frequenze comprese tra f1 ed f2 per le quali il processo utile prevale sul rumore e vale invece 0 altrove. La qualità che ne risulta è 
ed è massimizzata per 
. Il filtro fisicamente realizzabile presenta una attenuazione di 6dB alle frequenze di taglio e determina un rapporto segnale-rumore maggiore rispetto a quel che si avrebbe con il filtro rettangolare.
Stimatore lineare non polarizzato
Se abbiamo un processo ricevuto con parte utile strettamente limitata nella banda B = fM – fm , possiamo ridurre il rumore generando però distorsione utilizzando un filtro con banda B12 < B .
Se lo scopo è invece ridurre la distorsione, lo stimatore deve essere non polarizzato ossia deve essere un filtro con frequenze di taglio che coincidono con gli estremi della banda utile, in tal caso infatti la qualità della stima 
viene a coincidere con il rapporto segnale-rumore all´uscita Q .
Tale stimatore è noto anche in assenza di conoscenza della densità spettrale di potenza utile e la sua qualità si ricava immediatamente , è pertanto preferito agli altri stimatori anche perché al crescere della qualità della stima, i risultati differiscono di poco.