Processo aleatorio
1) Densità di probabilità del 1° ordine :
![]() esprime la probabilità che al tempo t1 sia X1 compresa tra x1 ed x1+dx1 .
esprime la probabilità che al tempo t1 sia X1 compresa tra x1 ed x1+dx1 .
2) Funzione cumulativa di probabilità :
![]()
dove p(x1,t1) rappresenta la densità di probabilità ossia la probabilità che al tempo t la variabile aleatoria X1 sia compresa tra x1 e x1+dx1 .
3) Densità di probabilità del 2° ordine :
![]() esprime la probabilità che al tempo t1 sia X1 compresa tra x1 ed x1+dx1 ed al tempo t2 sia X2 compresa tra x2 ed x2+dx2 .
esprime la probabilità che al tempo t1 sia X1 compresa tra x1 ed x1+dx1 ed al tempo t2 sia X2 compresa tra x2 ed x2+dx2 .
4) Densità di probabilità condizionata di ordine n :
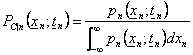
5) Momento statistico :
![]()
Si tratta di una espressione generale dalla quale per :
f(x) = x si ha il valor medio
f(x) = (x-hx) si ha il momento centrale del 1° ordine
f(x) = (x-hx)2 si ha il momento centrale del 2° ordine
6) Valore medio :
Si tratta del momento statistico di ordine 1 ![]() .
.
7) Varianza :
È il momento centrale di secondo ordine ![]() .
.
8) Momento della coppia di processi aleatori :
![]()
9) Funzione di autocorrelazione del processo aleatorio :
![]()
10) Funzione di autocovarianza del processo aleatorio :
![]()
11) Valore medio temporale :
![]()
si tratta di una quantità che viene introdotta al fine di evitare la dipendenza dal tempo, è riferito ad una particolare realizzazione del processo in esame.
12) Potenza media temporale :
![]()
si tratta di una quantità che viene introdotta al fine di evitare la dipendenza dal tempo, è riferito ad una particolare realizzazione del processo in esame.
13) Funzione di autocorrelazione temporale :
![]()
si tratta di una quantità che viene introdotta al fine di evitare la dipendenza dal tempo, è riferito ad una particolare realizzazione del processo in esame.
14) Processo stazionario in senso stretto :
È un processo per il quale ogni densità di probabilità congiunta risulta invariante rispetto ad un´arbitraria traslazione temporale per qualsiasi ordine n.
15) Processo stazionario in senso lato :
È un processo per il quale le densità di probabilità congiunte di 1° e 2° ordine risultano invarianti rispetto ad un´arbitraria traslazione temporale, si ha infatti :
a) p(x;t) = p(x) b) p2(x1,x2;t1,t2) = p2(x1,x2;t) essendo t = t2 - t1
per un processo stazionario in senso lato si ha che il valor medio statistico e la varianza sono costanti mentre le funzioni di autocorrelazione e autocovarianza dipendono solo da t.
16) Densità spettrale di potenza del processo stazionario :
Si tratta della media statistica delle densità spettrali di potenza delle realizzazioni ![]()
dove XT(f) è la trasformata di Fourier della generica realizzazione troncata xT(t) .
17) Prima relazione di Wiener - Khinchine :
![]()
18) Processo bianco :
È un processo che presenta densità spettrale di potenza costante su tutto la asse delle frequenze ![]() , è chiaramente un'astrazione in qunato ciò significa potenza infinita
, è chiaramente un'astrazione in qunato ciò significa potenza infinita
19) Processo stazionario ergodico :
È un processo per il quale la singola realizzazione, osservata sull´intero asse dei tempi, assomma tutte le proprietà statistiche del processo aleatorio.
20) Funzione di intercorrelazione :
![]()
21) Funzione di intercovarianza :
![]()
22) Funzione di intercovarianza normalizzata:
![]()
23) Densità spettrale di potenza incrociata :
![]()
24) Seconda relazione di Wiener - Khinchine :
![]()
25) Processi incoerenti :
La loro funzione di intercorrelazione Rxy(t) è nulla per ogni t.
26) Processi incorrelati :
La loro funzione di intercovarianza Kxy(t) è nulla per ogni t
27) Processi ortogonali :
E´ nullo il valore della funzione di intercorrelazione per t = 0 cioè Rxy(0)=0 .
28) Densità spettrale di potenza di un processo y(t) funzione di un processo x(t) :
![]()
dove H(f) è la funzione di trasferimento della trasformazione equivalente alla trasformata di Fourier della risposta impulsiva.
29) Processo gaussiano :
È un processo del quale si ha la piena conoscenza statistica qualora sia nota la funzione densità di probabilità del secondo ordine.
