Processi ciclostazionari
1) Processo ciclostazionario in senso stretto :
È un processo non stazionario per il quale esiste un numero reale T0>0, detto periodo di ciclostazionarietà, tale che la densità di probabilità congiunta verifichi la  dove con xn' si intende xn al tempo t1+T0 .
dove con xn' si intende xn al tempo t1+T0 .
Si ha che tutti i momenti statistici del processo ciclostazionario sono funzioni periodiche con periodo T0 .
2) Processo ciclostazionario in senso lato :
È un processo non stazionario per il quale le densità di probabilità del 1° e del 2° ordine risultano periodiche nel tempo e conseguentemente anche il valor medio statistico e la funzione di autocorrelazione che pertanto possono essere sviluppati in serie di Fourier 
 dove
dove  è la frequenza ciclica.
è la frequenza ciclica.
3) Valor medio ciclico :

4) Funzione di autocorrelazione ciclica :

5) Densità spettrale di potenza ciclica :
Considerando una singola realizzazione si ha

dove XT(f,t0) è la trasformata di Fourier della restrizione del processo x(t) ad una durata T intorno a t0 mentre  è la frequenza ciclica.
è la frequenza ciclica.
6) Prima relazione di Wiener Khinchine generalizzata :

7) Processo cicloergodico in senso stretto :
È un processo per il quale tutte le medie temporali coincidono con le corrispondenti medie statistiche mediate sul periodo.
8) Processo cicloergodico in senso lato :
È un processo per il quale le medie temporali di1° e 2° ordine coincidono con le corrispondenti medie statistiche mediate sul periodo, in particolare si ha  e
e  .
.
9) Funzione di intercorrelazione ciclica :
Nel caso di due processi ciclostazionari in senso lato con lo stesso periodo T0 , si ha
 .
.
10) Densità spettrale di potenza incrociata ciclica :

11) Seconda relazione di Wiener Khinchine generalizzata :

12) Processi stazionari e ciclostazionari in alta frequenza :
L'autocorrelazione del processo in alta frequenza x(t) può essere espressa in termini dei processi in banda base a valor medio nullo xp(t) in fase ed xq(t) in quadratura, si ha 

si nota quindi che indipendentemente dai processi xp(t) ed xq(t) il processo in alta frequenza x(t) risulta essere ciclostazionario in senso lato con periodo  . La media temporale della funzione di autocorrelazione è
. La media temporale della funzione di autocorrelazione è  cui corrisponde una densità spettrale di potenza
cui corrisponde una densità spettrale di potenza  .
.
Si possono avere i due seguenti casi particolari :
a) se i processi in banda base sono stazionari allora anche x(t) è stazionario e si ha  e
e 
pertanto l'autocorrelazione si riduce a  e quindi la densità spettrale di potenza è
e quindi la densità spettrale di potenza è  .
.
Si osservi che per t =0 si ottiene per le densità di potenza  e per le varianze
e per le varianze  quindi xp ed xq sono processi ortogonali e la loro densità di probabilità congiunta è il prodotto delle singole densità di probabilità, nel caso esse siano gaussiane si ha
quindi xp ed xq sono processi ortogonali e la loro densità di probabilità congiunta è il prodotto delle singole densità di probabilità, nel caso esse siano gaussiane si ha  ed essendo
ed essendo  e
e  si può fare un cambio di coordinate con Jacobiano J= r che restituisce
si può fare un cambio di coordinate con Jacobiano J= r che restituisce  , saturando rispetto a j si ottiene
, saturando rispetto a j si ottiene  ossia una densità di probabilità di tipo Rayleigh mentre saturando rispetto ad r si trova
ossia una densità di probabilità di tipo Rayleigh mentre saturando rispetto ad r si trova  ossia una densità di probabilità di tipo uniforme quindi la coppia di variabili è statisticamente indipendente. Inoltre la densità di probabilità del processo potenza istantanea
ossia una densità di probabilità di tipo uniforme quindi la coppia di variabili è statisticamente indipendente. Inoltre la densità di probabilità del processo potenza istantanea  è esponenziale
è esponenziale  .
.
b) se i processi in banda base sono ciclostazionari e supponendo per semplicità xq(t)=0 , la funzione di autocorrelazione è  la cui autocorrelazione media è
la cui autocorrelazione media è  cui corrisponde la densità spettrale di potenza
cui corrisponde la densità spettrale di potenza  quindi allo spettro del segnale in alta frequenza corrispondono anche gli spettri ciclici del segnale in banda base.
quindi allo spettro del segnale in alta frequenza corrispondono anche gli spettri ciclici del segnale in banda base.
13) Proprietà statistiche dell'oscillazione armonica in presenza di rumore gaussiano :
L'espressione del processo in alta frequenza in presenza di un'oscillazione armonica pura è  con
con  , vengono inoltre definite l'autocorrelazione
, vengono inoltre definite l'autocorrelazione  e la funzione di pseudocorrelazione
e la funzione di pseudocorrelazione  che consentono di scrivere l'autocorrelazione di x(t) nella forma
che consentono di scrivere l'autocorrelazione di x(t) nella forma 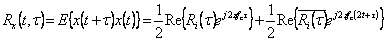 che risulta essere periodica con periodo
che risulta essere periodica con periodo  quindi il processo è ciclostazionario in senso lato come era prevedibile per la presenza della componente armonica.
quindi il processo è ciclostazionario in senso lato come era prevedibile per la presenza della componente armonica.
L'autocorrelazione media è  la cui trasformata di Fourier è la densità spettrale di potenza ed evidenzia la sovrapposizione tra lo spettro dell'oscillazione armonica e lo spettro del rumore in alta frequenza. Se i processi in banda base sono gaussiani , si ha la densità di probabilità congiunta
la cui trasformata di Fourier è la densità spettrale di potenza ed evidenzia la sovrapposizione tra lo spettro dell'oscillazione armonica e lo spettro del rumore in alta frequenza. Se i processi in banda base sono gaussiani , si ha la densità di probabilità congiunta  dove
dove  , tramite il cambio di coordinate
, tramite il cambio di coordinate  ,
,  avente Jacobiano J = r si giunge alla forma
avente Jacobiano J = r si giunge alla forma che, saturata rispetto a j restituisce
che, saturata rispetto a j restituisce  mentre saturata rispetto ad r dà
mentre saturata rispetto ad r dà  con
con  , infine la densità di probabilità del processo potenza istantanea è
, infine la densità di probabilità del processo potenza istantanea è  .
.
14 ) Spettro di potenza di segnale in banda base :
Si assuma un segnale di potenza in banda base  dove ak è un processo discreto stazionario in senso lato con statistiche hA , RA , s2A mentre q(t) è un segnale d'energia con trasformata di Fourier Sq(f) ed energia
dove ak è un processo discreto stazionario in senso lato con statistiche hA , RA , s2A mentre q(t) è un segnale d'energia con trasformata di Fourier Sq(f) ed energia  . Il valore medio di x(t) è
. Il valore medio di x(t) è  ed è quindi periodico con periodo Ts come pure la funzione di autocorrelazione
ed è quindi periodico con periodo Ts come pure la funzione di autocorrelazione 
da cui integrando su Ts si ottiene l'autocorrelazione ciclica con v=0 che con un cambio di variabile si riporta alla forma  (…dove eq(t) è l'autocorrelazione del segnale d'energia q(t) ) che valutata per t=0 e sostituendo
(…dove eq(t) è l'autocorrelazione del segnale d'energia q(t) ) che valutata per t=0 e sostituendo  fornisce la potenza
fornisce la potenza  mentre la densità spettrale di potenza si ottiene trasformando secondo Fourier la Rx(t) , si ottiene
mentre la densità spettrale di potenza si ottiene trasformando secondo Fourier la Rx(t) , si ottiene  ossia uno spettro a righe sovrapposto ad uno spettro distribuito.
ossia uno spettro a righe sovrapposto ad uno spettro distribuito.
Si osservi che se il processo {ak}è bianco oppure se q(t) è a repliche ortogonali, la potenza del processo ciclostazionario x(t) è pari al rapporto tra l'energia della forma d'onda deterministica ed il periodo Ts cioè  .
.
15) Segnale in banda base generalizzato :
La forma più generale di segnale in banda base x(t) si ottiene come combinazione di M forme d'energia xj ciascuna estratta con probabilità a priori Pi e con cadenza Ts , si ha cioè  , su di esso viene definito il simbolo medio
, su di esso viene definito il simbolo medio  che nel caso i segnali vengano rappresentati nello spazio dei segnali coincide con il baricentro della costellazione dei simboli. Lo spettro che ne risulta è dato dalla sovrapposizione di uno spettro continuo e di uno spettro distribuito, quest'ultimo può essere interpretato come spettro di potenza della forma d'onda periodica
che nel caso i segnali vengano rappresentati nello spazio dei segnali coincide con il baricentro della costellazione dei simboli. Lo spettro che ne risulta è dato dalla sovrapposizione di uno spettro continuo e di uno spettro distribuito, quest'ultimo può essere interpretato come spettro di potenza della forma d'onda periodica  che coincide con il valore atteso di x(t) ossia
che coincide con il valore atteso di x(t) ossia  e che essendo periodica può essere scomposta in serie di Fourier
e che essendo periodica può essere scomposta in serie di Fourier  dove Sa(f) è la trasformata di Fourier del simbolo medio
dove Sa(f) è la trasformata di Fourier del simbolo medio  il cui modulo quadro restituisce la densità spettrale di potenza a righe
il cui modulo quadro restituisce la densità spettrale di potenza a righe  e quindi si nota che lo spettro del segnale periodico è discreto e possiede righe multiple intere della frequenza di simbolo.
e quindi si nota che lo spettro del segnale periodico è discreto e possiede righe multiple intere della frequenza di simbolo.
16) Rappresentazione geometrica dei processi aleatori
Un processo aleatorio x(t) a valor medio nullo può essere rappresentato in un intervallo finito  tramite lo sviluppo in serie
tramite lo sviluppo in serie  dove yk(t) è un insieme di n funzioni ortonormali nell'intervallo
dove yk(t) è un insieme di n funzioni ortonormali nell'intervallo  mentre {ck} è un processo aleatorio discreto a valor medio nulo, se quest'ultimo presenta correlazione
mentre {ck} è un processo aleatorio discreto a valor medio nulo, se quest'ultimo presenta correlazione  lo sviluppo è detto in serie di Karhunen-Loeve.
lo sviluppo è detto in serie di Karhunen-Loeve.
Col fine di trovare un'equazione che consenta di determinare le yk(t) si calcola l'intercorrelazione tra i processi x(t) e ck , si ha  del resto per i coefficienti ck si può scrivere la relazione
del resto per i coefficienti ck si può scrivere la relazione  , sostituendola nel calcolo dell'intercorrelazione si ha
, sostituendola nel calcolo dell'intercorrelazione si ha  uguagliando le due espressioni trovate si ottiene un sistema di equazioni alle autofunzioni
uguagliando le due espressioni trovate si ottiene un sistema di equazioni alle autofunzioni  cui debbono soddisfare le autofunzioni di base yk(t) .
cui debbono soddisfare le autofunzioni di base yk(t) .
L'uguaglianza  è un'uguaglianza tra processi e deve verificare la convergenza in media quadratica
è un'uguaglianza tra processi e deve verificare la convergenza in media quadratica  tuttavia nel caso dello sviluppo KL si ha
tuttavia nel caso dello sviluppo KL si ha  che si dimostra essere condizione necessaria e sufficiente affinchè sia rispettata la convergenza in media quadratica. Tramite le sostituzioni
che si dimostra essere condizione necessaria e sufficiente affinchè sia rispettata la convergenza in media quadratica. Tramite le sostituzioni
 ,
,  ,
,  ,
,  ,
, 
il sistema di equazioni viene normalizzato ossia ricondotto all'intervallo [-1 , 1 ] , si ha :
 dove le ck sono funzioni ortogonali nell'intervallo [-1,1].
dove le ck sono funzioni ortogonali nell'intervallo [-1,1].
Si fanno i due seguenti esempi di applicazione :
a) Rappresentazione di rumore bianco in un intervallo finito
La funzione di autocorrelazione di x(t) è  con
con  essendo Nx la densità spettrale del processo bilatero, sostituendo si ottiene il sistema di equazioni
essendo Nx la densità spettrale del processo bilatero, sostituendo si ottiene il sistema di equazioni  che ha come soluzione delle funzioni dette sferoidali schiacciate.
che ha come soluzione delle funzioni dette sferoidali schiacciate.
b) Rappresentazione di rumore bianco di durata infinita
La funzione di autocorrelazione di x(t) è  con
con  essendo Nx la densità spettrale del processo bilatero, però in questo caso si fa tendere ad infinito l'intervallo di integrazione, sostituendo nella
essendo Nx la densità spettrale del processo bilatero, però in questo caso si fa tendere ad infinito l'intervallo di integrazione, sostituendo nella  e sfruttando la relazione
e sfruttando la relazione  si ottiene qk = Nx e quindi il processo {ck} risulta stazionario in senso lato, si trova inoltre che è verificata la relazione
si ottiene qk = Nx e quindi il processo {ck} risulta stazionario in senso lato, si trova inoltre che è verificata la relazione  e quindi si ha la convergenza in media quadratica.
e quindi si ha la convergenza in media quadratica.

 .
. ed essendo
ed essendo  , saturando rispetto a
, saturando rispetto a  ossia una densità di probabilità di tipo Rayleigh mentre saturando rispetto ad r si trova
ossia una densità di probabilità di tipo Rayleigh mentre saturando rispetto ad r si trova  .
. .
. mentre la densità spettrale di potenza si ottiene trasformando secondo Fourier la Rx(
mentre la densità spettrale di potenza si ottiene trasformando secondo Fourier la Rx( ossia uno spettro a righe sovrapposto ad uno spettro distribuito.
ossia uno spettro a righe sovrapposto ad uno spettro distribuito. 