Vibrazioni reticolari

1) Velocità di gruppo :

Si tratta della derivata della pulsazione angolare w rispetto al vettore d´onda k,     .

 

2) Caratteristiche di un´onda elastica propagantesi in una catena formata da atomi uguali :

Si suppone un potenziale di tipo elastico dove x è lo spostamento quindi la forza agente è .

Consideriamo una catena lineare di atomi posti a distanza a tra di loro, la forza che agisce sulla atomo nella posizione s dovuta alla atomo nella posizione s+p è proporzionale tramite la costante C_p alla differenza dei loro spostamenti u_s e u_s+p rispetto alle posizioni di equilibrio    .

Considerando come origine l´inizio della catena e ricercando soluzioni di tipo sinusoidale  e sostituendo nell´equazione differenziale si ha   e dividendo per   si ottiene  dove si è considerata l´interazione con gli atomi a destra uguale all´interazione con gli atomi a sinistra. Se ci si limita alla interazione con i soli primi vicini quindi p =1 e si scrive il termine dentro parentesi come un seno, si ottiene la relazione di dispersione   .

 

3) 1ª zona di Brillouin :

Scrivendo il rapporto tra il valore dello spostamento in un punto u_s+p+1 ed il valore dello spostamento nel punto precedente u_s+p si trova e^ika che è una quantità periodica con periodo 2p della quale ci interessano sia valori positivi che valori negativi perchè le onde possono propagarsi sia a destra che a sinistra quindi -p £ ka £ p essendo a la distanza tra 2 atomi della catena. Si ha  che rappresenta la prima zona di Brillouin.

 

4) Caratteristiche della relazione di dispersione :

Abbiamo visto viene ricavata considerando la sola interazione con i primi vicini nel caso di una catena formata da atomi uguali, si ha    dalla quale si può ricavare la velocità di gruppo 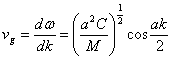 da cui si nota che in corrispondenza al bordo di zona   si ha v_g=0 e quindi siamo in presenza di un´onda stazionaria.

 

5) Rapporto tra v_g , v_s  e la relazione di dispersione :

la velocità di gruppo si può ricavare dalla relazione di dispersione 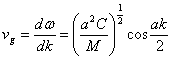 . Per k piccoli ossia nella banda acustica si ha che il grafico della relazione di dispersione è assimilabile ad una retta e quindi

 

6) Caratteristiche di un´onda elastica propagantesi in una catena formata da 2 atomi aventi masse diverse :

Si suppone di avere una catena lineare costituita da un´alternanza di atomi con massa M₁ e di atomi con massa M₂ , l´interazione della atomo con massa M₁ posto in posizione 2s+1 con i primi vicini è data dall´equazione differenziale  :

Analogamente l´interazione della atomo con massa M₂ posto in posizione 2s con i primi vicini è data dall´equazione :

Si tratta di 2 equazioni differenziali per le quali cerchiamo soluzioni nella forma di due sinusoidi aventi stessa pulsazione ma ampiezze diverse per gli atomi aventi masse diverse ossia   e    le quali sostituite nelle equazioni differenziali danno un sistema nelle incognite x ed h il quale ha soluzione solo se il determinante si annulla ossia se   dalla quale si ricava che per ogni w esistono 2 diversi valori di k ed analogamente per ogni k esistono 2 diversi valori di w in particolare la soluzione con il segno + va a descrivere le w più elevate corrispondenti alla branca ottica che assume il valore massimo per k=0 ed il valore minimo sui bordi di zona. La soluzione con il – individua invece la branca acustica che è molto simile alla curva di dispersione trovata nel caso di una catena di atomi identici. Tra le 2 branche vi è una branca proibita.

 

7) Prima zona di Brillouin nel caso di una catena formata da 2 atomi aventi masse diverse :

Scrivendo il rapporto tra il valore dello spostamento in un punto u_s+p+2 ed il valore dello spostamento nel punto precedente avente la stessa massa u_s+p si trova e^ik2a che è una quantità periodica con periodo 2p della quale ci interessano sia valori positivi che valori negativi perchè le onde possono propagarsi sia a destra che a sinistra quindi -p £ 2ka £ p essendo 2a la distanza tra 2 atomi della catena aventi la stessa massa, in formule si ha  .

 

8) Caratteristica dei modi ottici :

Ponendo k=0 nell´equazione della branca ottica e sostituendo in essa le equazioni del sistema in x ed h si trova    quindi gli atomi vibrano in opposizione di fase.

 

9) Caratteristica dei modi acustici :

Ponendo k=0 nell´equazione della branca acustica e sostituendo in essa le equazioni del sistema in x ed h si trova x=h    quindi gli atomi vibrano in fase.

 

10) Condizioni al contorno di Karmann :

Il campione è limitato quindi dobbiamo supporre di unire gli estremi e quindi richiedere che l´onda  assuma lo stesso valore sia all´inizio della catena per s=0 che alla fine per s=L. Si ha   la quale è verificata solo per  quindi si ha una quantizzazione sui k. Per trovare il numero n dei k consentiti nella 1ª zona basta moltiplicare la densità di stati in k ad unità di lunghezza  per la lunghezza della 1ª zona  , si ha    pari cioè al numero di atomi quindi i k sono quantizzati ma approssimano un continuo. Analogamente si può dividere la ampiezza della 1ª zona  per la distanza tra due k consentiti .