Proprietà termiche degli isolanti

1) Capacità termica a volume costante e suo grafico classico :

È definita come la derivata parziale della energia interna E rispetto alla temperatura T a volume costante . Per la meccanica classica, l´energia interna di ogni atomo si calcola associando ad ognuno dei suoi 6 gradi di libertà (3 vibrazionali e 3 traslazionali) una energia  pertanto considerando una mole di atomi l´energia interna è  e pertanto   quindi costante con la temperatura. Confrontandola con i rilevamenti sperimentali si ottiene che questa rappresentazione è sostanzialmente corretta ad alte temperature mentre alle basse, la capacità termica tende a 0 e lo fa come T³ , per spiegare tale comportamento occorre considerare l´energia interna dovuta ai soli fononi, per ognuno di essi si ha   quindi l´energia totale è   dove 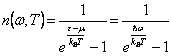   (dove m =0 in quanto i fononi sono particelle prive di massa) è la funzione di occupazione di Bose che descrive il n° di fononi che ad una data temperatura possiedono la pulsazione w_k ma abbiamo visto che i k contenuti nella 1ª zona approssimano un continuo quindi si può sostituire la sommatoria con un integrale. La difficoltà di tale integrale risiede nella D(w) , essa può essere ricavata sperimentalmente e l´integrale calcolato numericamente oppure si utilizzano le approssimazioni di Einstein e di Debye.

 

2) N° di occupazione dei fononi :

I fononi sono dei bosoni quindi il numero dei fononi che ad una data temperatura posseggono una data energia è dato dalla statistica di Bose Einstein               . Una considerazione importante da fare che è alla base della ipotesi di Debye è che quando T®0 si ha che il numero dei fononi è elevato per w piccole e quindi dalla relazione di dispersione, per k piccoli.

 

3) Densità lineare di stati in k :

Abbiamo ricavato dalle condizioni al contorno di Karmann che la distanza tra due k consentiti consecutivi è  , per trovare la densità w(k) dei k basta farne il reciproco ottenendo  .

 

4) Ipotesi di Einstein :

Einstein propone una densità di stati in w del seguente tipo  , ossia che ogni fonone possieda la stessa pulsazione w=w_einstein=w_e quindi considerando una mole N di fononi, ciascuno dei quali (se vale la legge di Hooke) possiede 3 modi indipendenti di vibrazione ( 2 trasversali ed uno longitudinale)  si ha   da cui si ha  da essa si vede che per T®¥ si può sviluppare in serie l´esponenziale e si trova C_v®3Nk=3R   mentre per T®0 l´esponenziale al denominatore diverge e quindi C_v®0 come un esponenziale e non come T³ che è il valore sperimentale, questo è dovuto alla cattiva approssimazione della D(w) che tuttavia per alte temperature è da preferire alla approssimazione di Debye.

5) Espressione della densità di stati in w nel caso di una catena lineare :

Osservando la curva di dispersione occorre mettere in relazione la densità di stati in w D(w) con la densità di stati in k  si ha   allora     . Sostituendo l´espressione della V_g che si ottiene dalla relazione di dispersione si vede che la D(w) diverge ad ¥ in corrispondenza alla asintoto verticale w = w_max . Con la approssimazione di Debye si trova che la D(w) è costante sino al valore w_D .

 

6) Ipotesi di Debye :

Debye osserva dalla funzione di occupazione di Bose 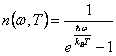 che a basse temperature (..sono le temperature che interessano perché per esse la capacità classica è sbagliata) ci sono molti fononi con k piccolo, ma in queste regioni la curva di dispersione può essere approssimata con 2 rette tangenti al limite per k®0. Gli effetti di questa approssimazione sono 2 :

a)       Ricordando che   si ha  costante e quindi può essere portato fuori dall´integrale della C_v .

b)       Cambiano gli estremi di integrazione in quanto la retta tangente incontra la verticale passante per il bordo di zona per w_D > w_max     si ha    w_D =1,57 w_max     .

Svolgendo i calcoli si trova C_v®0 come T³ .

 

7) Densità superficiale di stati in k :

È   , si ottiene in maniera analoga al caso unidimensionale.

 

8) Considerazioni sulla approssimazione di Debye nel caso bidimensionale :

Si scrive la D(w) considerando delle linee ad w costante , si ottiene 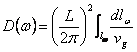  , per semplificarla secondo Debye si pone v_g = v_s e si porta fuori dall´integrale ed inoltre si approssima la curva di dispersione con un cerchio di raggio k quindi  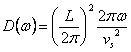che sostituita nell´integrale consente di calcolare l´energia interna. Si noti che l´estremo superiore della integrale è la w_D che si ottiene uguagliando il numero di fononi al prodotto tra la densità di fononi ad unità di superficie per la area della circonferenza di Debye. Come risultato si ottiene che la densità di stati è crescente in w sino alla w corrispondente al bordo della 1ª zona dopodichè decresce sino a valere 0 in corrispondenza al valore del raggio della circonferenza approssimante.

 

9) Densità volumica di stati in k :

È   , si ottiene in maniera analoga al caso unidimensionale.

 

10) Considerazioni sulla approssimazione di Debye nel caso tridimensionale :

Si scrive la D(w) considerando le superfici ad w costante , si ottiene   , per semplificarla secondo Debye si pone v_g = v_s e si porta fuori dall´integrale ed inoltre si approssima la curva di dispersione con una sfera di raggio k quindi 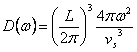 che sostituita nell´integrale consente di calcolare l´energia interna. Si noti che l´estremo superiore della integrale è la w_D che si ottiene uguagliando il numero di fononi al prodotto tra la densità di fononi ad unità di volume e il volume della sfera di Debye. Come risultato si ottiene che la densità di stati è crescente quadraticamente in w.

 

11) Temperatura di Debye :

È una misura della forza del legame che caratterizza il reticolo, maggiore è la temperatura di Debye, maggiore è la forza del legame. Si ottiene dalla relazione  , è pertanto la temperatura che corrisponde all´w_D .

 

12) Cause della dilatazione termica dei solidi :

Le forze di interazione tra 2 atomi non sono descritte da un oscillatore armonico quindi da una parabola  poiché ad esso corrisponde una  lineare per la quale quindi vale la sovrapposizione degli effetti bensì da una funzione più complessa e soprattutto asimmetrica, quindi un atomo che a seguito della somministrazione di calore oscilla intorno alla posizione di equilibrio, lo fa in maniera asimmetrica nelle 2 direzioni e quindi lo spostamento medio è non nullo e quindi la catena lineare si dilata.

 

13) Coefficiente di conduttività termica K :

È il coefficiente di proporzionalità K tra la quantità di calore Q che fluisce in un materiale ed il gradiente di temperatura in esso presente, si ha  . Per ricavare il valore di K si osserva che la quantità di calore trasportata da n particelle aventi ciascuna capacità termica c è  , del resto  dove t è il tempo di rilassamento ossia il tempo che intercorre tra 2 urti successivi, inoltre considerando una superficie unitaria si ha che nell´unità di tempo è attraversata da n|v_x| fononi complessivamente nei due versi quindi si ha  dove si è supposta l´isotropia quindi . Essendo l=vt il libero cammino medio e C=nc la capacità termica totale del sistema si ha quindi .

 

14) Libero cammino medio dei fononi :

È la distanza media che essi percorrono tra un urto ed il successivo, è funzione delle seguenti cause :

a)       Presenza nel reticolo di atomi diversi quali isotopi o impurità

b)       Limitatezza fisica del reticolo

c)       Urto tra fononi

 

15) Leggi di conservazione in un urto tra fononi :

                  Legge di conservazione del quasi momento

                   Legge di conservazione della energia

Attenzione, non è necessario che il numero di fononi si conservi.

 

16) Tipologie di urti tra fononi e libero cammino medio :

Quando 2 fononi si vengono a trovare nella stessa regione spaziale, si ha un urto nel quale si deve conservare la quantità di energia e l´impulso, si possono verificare i 2 seguenti tipi di urto:

a)       Urto normale si ha quando il k risultante dalla somma vettoriale dei k dei fononi incidenti è contenuto nella 1ª zona quindi il fonone risultante è ancora nella direzione del moto e contribuisce alla conduzione termica.

b)       Urto Umklapp si ha quando il k risultante dalla somma vettoriale dei k dei fononi incidenti esce dalla 1ª zona ma sottraendogli un vettore del reticolo reciproco si ottiene un fonone con un k tale da opporsi al moto. I fononi utili sono quelli che hanno k prossimi al bordo della 1ª zona, il loro numero cresce linearmente con la temperatura infatti   quindi la conducibilità termica descresce linearmente con la temperatura.

 

17) Imperfezioni e libero cammino medio :

L´effetto delle imperfezioni ha luogo unicamente quando il cammino libero medio dovuto ai processi di Umklapp è paragonabile alle dimensioni fisiche del cristallo, quindi il libero cammino medio è costante con la temperatura.

 

18) Valore della conducibilità termica in funzione della temperatura per un isolante :

Occorre analizzare la variazione del coefficiente di conduttività termica  con la temperatura, si ha che ad alte temperature predomina il processo di Umklapp in quanto i fononi efficaci crescono al crescere della temperatura, a temperature prossime alla temperatura di Debye q_D il numero di fononi efficaci decresce come un esponenziale negativo, mentre se T®0 il numero di fononi efficaci tende a zero e quindi il libero cammino medio è costante in quanto imposto dalle imperfezioni e dalle dimensioni del cristallo che sono costanti, e domina pertanto la capacità termica C la quale spinge la conduttività termica a zero come T³.

 

19) Tipologie di sonde utilizzabili per analizzare le caratteristiche dei fononi :

a)       l´elettrone il quale ha il problema di non essere neutro e quindi è valido solo per una analisi superficiale del materiale.

b)       la radiazione elettromagnetica ed in particolare i raggi x .

c)       i neutroni i quali reagiscono debolmente ai campi magnetici ma sono difficili da generare e da fermare.