Diffrazione dei cristalli e reticolo reciproco

1)    Condizione di Bragg :

È la condizione da imporre alla lunghezza d´onda di una radiazione incidente con un angolo q rispetto alla asse x affinché possa dar luogo ad interferenza costruttiva se inviata contro dei piani reticolari separati dalla distanza d.  La condizione 

si ottiene individuando il piano reticolare immediatamente sottostante, disegnando il raggio che riflette su di esso e valutando la lunghezza ottica in più rispetto alla riflessione sul piano sovrastante. Affinchè i due raggi siano in fase occorre che tale differenza di percorso sia un multiplo n della lunghezza d´onda l.

 

2) Calcolo di Laue per la ampiezza della onda diffusa :

Si tratta di un calcolo che viene introdotto per limitare l´errore di base del calcolo di Bragg, ossia il considerare i piani reticolari come degli specchi e quindi perfettamente riflettenti.

Si consideri uno dei punti del reticolo come origine O , un punto situato a distanza r da esso viene investito da un´onda piana  che considereremo sempre al tempo t = 0 . In r si ha   ma questo punto diviene sorgente di onde sferiche secondarie per cui la ampiezza della radiazione sul rivelatore posto a distanza r da r e R dall´origine è   dove kr sono i moduli perché in un´onda sferica i due vettori sono sempre paralleli.

Scriviamo r in funzione delle altre grandezze      e quindi si ha 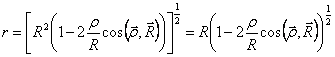     dove r<<R in quanto il cristallo ha dimensioni infinitesime, allora sviluppando in serie di Taylor si ha   che sostituito nell´esponenziale dà    il termine e^ikR  può essere trascurato in quanto costante su tutto il volume mentre    essendo   il vettore nella direzione che congiunge l´origine con il rivelatore ed avente come modulo k .  Si ha   dove Dk è il vettore di scattering.

Naturalmente al rivelatore giungono anche i contributi degli altri punti del reticolo   .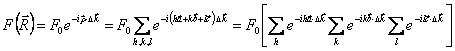

Se ad esempio nel reticolo ci sono M atomi e consideriamo solo la prima sommatoria si ha : 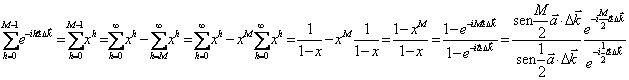 dove ho raccolto l´esponenziale con la metà della esponente.

Viene però rilevato il modulo quadro di questa grandezza   il massimo della quale si ottiene annullando il denominatore ossia per  e quindi   dove q è un intero.

Analogamente per le altre 2 sommatorie si trovano              .

Questo calcolo è però ancora imperfetto in quanto non tiene conto dello scattering multiplo.

 

3) Condizioni di Laue per la massima diffrazione :

Si ricavano dal precedente calcolo di Laue :

                                                            

dove q, r, s   sono dei numeri interi.

 

4) Vettori di traslazione del reticolo reciproco :

                                                                         

dove il denominatore rappresenta il volume della cella del reticolo cristallino.

La loro espressione è stata costruita in modo che una qualsiasi loro combinazione lineare soddisfi le equazioni di Laue per la massima diffrazione.

 

5) Condizione di diffrazione :

Si ha diffrazione secondo Laue quando il vettore di scattering risulta essere uguale ad uno qualsiasi dei vettori G del reticolo reciproco ossia  , non si deve dimostrare nulla in quanto i vettori di traslazione del reticolo reciproco ,, sono stati costruiti proprio in modo da soddisfare le equazioni di Laue. Questa legge può anche essere espressa in forma diversa infatti    allora   , elevando al quadrato si ha   ma trattandosi di scattering elastico si ha k^´=k e quindi l´equazione assume la forma   che è soddisfatta se k termina su di un piano normale a  nel punto di mezzo di .

 

6) Relazione tra reticolo reciproco e reticolo cristallino :

Ogni vettore del reticolo reciproco è ortogonale ad un piano del reticolo cristallino.

Consideriamo il piano che interseca gli assi del reticolo cristallino nei punti   ,   ,  ad esso appartengono i vettori  e   . Si dimostra che il loro prodotto vettoriale con un generico vettore   vale 0, si ottengono 3 equazioni che sono soddisfatte per  ,  ,   nelle quali si vede che i coefficienti di G corrispondono agli indici di Miller del reticolo cristallino.

 

7) Distanza tra due piani reticolari :

È data dalla relazione   dove h, k, l sono gli indici di Miller del piano a cui G è ortogonale. Da questa relazione si deduce che ad ogni punto del reticolo reciproco corrisponde una possibile riflessione del reticolo cristallino.

 

8) Relazioni tra le leggi di Bragg e quella di Laue :

Le due leggi sono equivalenti infatti 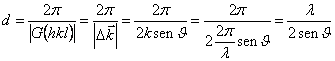 e quindi si ha  che è proprio la condizione di Bragg.

 

9) Prima zona di Brillouin :

Si tratta della cella di Wigner Seitz costruita sul reticolo reciproco.

 10) Sfera di Ewald :

Essendo    allora    quindi disegnando un vettore k che termini in un qualsiasi punto del reticolo reciproco e immaginando di farlo ruotare in modo da creare un cerchio o una sfera, se quest´ultima interseca un altro punto del reticolo reciproco, si forma un raggio diffratto, il vettore trovato è ortogonale al piano del reticolo cristallino rispetto al quale c´è riflessione.

 

11) Fattore di struttura geometrica :

La teoria di Laue è corretta nel caso ogni punto reticolare sia formato da un solo atomo ma se gli atomi sono più di uno, si dovrà considerare un fattore di struttura geometrica che tiene conto della posizione di questi atomi all´interno della cella unitaria questo fattore di correzione vale   dove f_j è il fattore di forma ed è una misura del potere di scattering della atomo j-esimo nella cella unitaria.