Bande di energia
1) Evoluzione del modello del gas di Fermi :
Il modello del gas di Fermi trascura 2 importanti fenomeni :
a) È ragionevole che vi sia una interazione elettrone-elettrone, gli si associa un potenziale ignoto ma costante.
b) È ragionevole che vi sia una interazione con gli ioni del reticolo, gli si associa un potenziale periodico in stretta analogia con la natura periodica con cui gli atomi si presentano nel reticolo in quanto si deve tener conto che l´elettrone subisce una forte repulsione da parte dei nuclei in virtù del principio di esclusione di Pauli, dato che in corrispondenza dei nuclei tutti gli stati sono occupati.
2) Equazione d´onda per un elettrone in un potenziale periodico :
Consideriamo un reticolo lineare nel quale gli atomi siano distanziati di a tra di loro. Nella equazione di Schroedinger ![]() si sostituiscono :
si sostituiscono :
a) la serie di Fourier della y(x) sommata sui soli k consentiti dalle condizioni al contorno ![]() .
.
b) La serie di Fourier del potenziale periodico u(x) sommato sui vettori G del reticolo reciproco 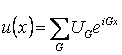 .
.
Ottenendo ![]() da cui
da cui ![]() avendo posto K´=G+K ma essendo un indice muto si può anche risostituire con K quindi ponendo
avendo posto K´=G+K ma essendo un indice muto si può anche risostituire con K quindi ponendo ![]() si ha
si ha 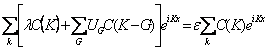 uguagliando i coefficienti delle 2 serie e portando tutto al 1° membro si ha
uguagliando i coefficienti delle 2 serie e portando tutto al 1° membro si ha  che è detto sistema di equazioni centrale.
che è detto sistema di equazioni centrale.
3) Teorema di Block :
Afferma che le autofunzioni della equazione di Schroedinger per un potenziale periodico hanno la forma ![]() ossia sono il prodotto di un´onda piana per un potenziale avente la stessa periodicità del reticolo.
ossia sono il prodotto di un´onda piana per un potenziale avente la stessa periodicità del reticolo.
Avevamo ipotizzato per la y(x) una forma del tipo ![]() .
.
Dal sistema di equazioni centrale si vede che i k permessi per la funzione d´onda, non sono un continuo ma sono della forma ![]() dove k è scelto a caso tra i k consentiti dalle condizioni al contorno. Si ha :
dove k è scelto a caso tra i k consentiti dalle condizioni al contorno. Si ha : 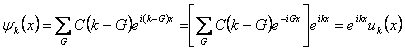 dove
dove ![]() è un potenziale periodico dato che la serie effettuata sui vettori del reticolo reciproco, è invariante per traslazione dello stesso.
è un potenziale periodico dato che la serie effettuata sui vettori del reticolo reciproco, è invariante per traslazione dello stesso.
4) Considerazioni sull´impulso per l´elettrone di Block :
Esso non verifica la relazione ![]() alla base della teoria di Schroedinger infatti si ha:
alla base della teoria di Schroedinger infatti si ha: ![]() quindi k non è il momento della elettrone di Block e viene pertanto chiamato quasi momento o momento cristallino.
quindi k non è il momento della elettrone di Block e viene pertanto chiamato quasi momento o momento cristallino.
5) Modello degli elettroni quasi liberi :
Considerando 2 equazioni tratte dal sistema di equazioni centrale che differiscono solo per un vettore G1 del reticolo reciproco, si ha  si noti che non ci sono le sommatorie relative all´energia potenziale perché nel modello degli elettroni quasi liberi si ipotizza che l´energia cinetica sia molto maggiore della energia potenziale, potremmo trascurarla completamente ma teniamo 2 termini per facilitare i calcoli, si ipotizza inoltre che il potenziale periodico sia una funzione pari quindi
si noti che non ci sono le sommatorie relative all´energia potenziale perché nel modello degli elettroni quasi liberi si ipotizza che l´energia cinetica sia molto maggiore della energia potenziale, potremmo trascurarla completamente ma teniamo 2 termini per facilitare i calcoli, si ipotizza inoltre che il potenziale periodico sia una funzione pari quindi ![]() . Il sistema precedente ha soluzioni solo se il determinante è 0, si trova che le radici sono
. Il sistema precedente ha soluzioni solo se il determinante è 0, si trova che le radici sono  , a questo punto se si sceglie come indice delle autofunzioni
, a questo punto se si sceglie come indice delle autofunzioni ![]() coincidono col bordo della 1ª zona, si ottiene
coincidono col bordo della 1ª zona, si ottiene ![]() e quindi
e quindi ![]() e
e ![]() . Sostituendo nelle equazioni di partenza si determina
. Sostituendo nelle equazioni di partenza si determina ![]() e
e ![]() e da esse le y che risultano essere 2 onde stazionarie una di tipo tipo coseno per la quale si ha che la densità di probabilità di trovare gli elettroni è massima in corrispondenza degli ioni positivi e quindi minimizza l´energia, mentre la altra è di tipo seno e la densità di probabilità di trovare gli elettroni è massima tra due ioni quindi è la soluzione ad energia più alta.
e da esse le y che risultano essere 2 onde stazionarie una di tipo tipo coseno per la quale si ha che la densità di probabilità di trovare gli elettroni è massima in corrispondenza degli ioni positivi e quindi minimizza l´energia, mentre la altra è di tipo seno e la densità di probabilità di trovare gli elettroni è massima tra due ioni quindi è la soluzione ad energia più alta.
6) Gap di energia :
È la banda di energie proibite che scaturisce dall´equazione della elettrone di Block. Abbiamo visto che sul bordo di zona si ha ![]() e
e ![]() quindi la gap vale 2u1 . Si noti che nel modello del gas di Fermi u1 = 0 e quindi la gap non c´è e si ha una parabola continua.
quindi la gap vale 2u1 . Si noti che nel modello del gas di Fermi u1 = 0 e quindi la gap non c´è e si ha una parabola continua.
7) Numero di stati in una banda :
Avevamo già visto che applicando le condizioni al contorno di Karmann si trova che il n° di k compatibili contenuti nella 1ª zona è proprio N pari cioè al numero di atomi di cui si compone la catena lineare, però gli elettroni sono fermioni quindi ci possono essere 2 elettroni con lo stesso k ma spin opposto, pertanto all´interno della 1ª zona ci sono 2N stati disponibili.
8) Determinazione dei metalli con la teoria delle bande :
Ognuno degli N atomi di un metallo può fornire un elettrone i quali in totale saranno N e quindi possono riempire solo la metà della 1ª banda composta da 2N stati liberi, questi elettroni sono quindi liberi di assorbire energia e passare a stati ad energia più elevata. In generale sono metalli tutti gli atomi con un numero dispari di elettroni di valenza.
9) Determinazione degli isolanti con la teoria delle bande :
Ognuno degli N atomi di un isolante può fornire due elettroni i quali in totale saranno 2N e quindi riempiono completamente la 1ª banda composta da 2N stati liberi, dato che gli stati liberi sono separati dalla cima della banda piena da un gap elevato, questi elettroni non possono assorbire quindi trasportare energia. In generale sono isolanti tutti gli atomi con un n° pari di elettroni di valenza.
10) Determinazione dei semiconduttori con la teoria delle bande :
Gli N atomi di semiconduttore hanno valenza media 4 quindi in totale ci sono 4N atomi e pertanto le prime 2 bande saranno completamente piene come per un isolante, dai quali però si distinguono in quanto la gap tra la 2ª e la 3ª banda è molto piccola, pertanto già a temperatura ambiente si hanno elettroni in banda di conduzione.
11) Schema della zona ridotta :
È una procedura che consiste nel far si che il vettore momento cristallino k indice della funzione di Block appartenga alla 1ª zona di Brillouin, il che è sempre possibile sommando un opportuno vettore G del reticolo reciproco.
12) Schema della zona ripetuta :
Si ottiene ripetendo spazialmente lungo la asse dei k, quanto si è ottenuto per i k della 1ª zona, si ottiene in tal modo una funzione eK periodica.
13) Schema della zona estesa :
Si ha che per ogni zona viene riportato il corretto valore della energia degli stati disponibili, senza cioè comprimere il tutto all´interno della 1ª zona.
14) Come disegnare la superficie di Fermi per gli elettroni liberi :
Si disegnano la 1ª , 2ª , 3ª zona col procedimento di Wiegner Seitz, poi si considera la circonferenza di Fermi la quale contiene interamente la 1ª zona, per le altre zone non si fa altro che individuare l´intersezione con la circonferenza di Fermi e traslare queste aree all´interno della 1ª zona in modo che creino un insieme connesso.
15) Come disegnare la superficie di Fermi per gli elettroni quasi liberi :
Si ricava prima la superficie di Fermi per gli elettroni liberi e poi occorre tener conto che al bordo di zona la vg si annulla e quindi il gradiente della energia rispetto a k vale 0 cioè non ci possono essere delle discontinuità, pertanto occorre smussare gli angoli.
16) Effetto di un campo elettrico E sull´elettrone di Block :
Applicando un campo![]() in una direzione, integrando la
in una direzione, integrando la ![]() si ha
si ha ![]() quindi k aumenta nel tempo in direzione opposta ad
quindi k aumenta nel tempo in direzione opposta ad![]() sino a che, giunto sul bordo di zona subisce Umklapp e ricompare dalla altro lato della 1ª zona ossia con un k negativo, si viene cioè a creare una corrente alternata, ciò in realtà non si verifica fondamentamente per la presenza di due cause le quali rendono il potenziale non periodico al contrario di quanto si afferma nell´ipotesi di Block :
sino a che, giunto sul bordo di zona subisce Umklapp e ricompare dalla altro lato della 1ª zona ossia con un k negativo, si viene cioè a creare una corrente alternata, ciò in realtà non si verifica fondamentamente per la presenza di due cause le quali rendono il potenziale non periodico al contrario di quanto si afferma nell´ipotesi di Block :
a) imperfezioni nel reticolo come lacune o impurità.
b) solo a 0K il reticolo è fermo mentre a temperature maggiori, il reticolo è in vibrazione e soltanto in media si ha la periodicità del reticolo stesso.
17) Moto di un elettrone in presenza di un campo magnetico :
Gli elettroni percorrono le linee di Fermi infatti si ha  e del resto
e del resto ![]() quindi la forza è sempre ortogonale al
quindi la forza è sempre ortogonale al ![]() ma esso è ortogonale alle superfici ad energia costante come appunto le linee di Fermi lungo le quali in definitiva si svolge il moto della elettrone. A seconda del verso di percorrenza si parla di orbita di tipo elettrone o di tipo lacuna. Si hanno orbite di tipo lacuna quando la cima di una banda piena possiede degli stati vuoti.
ma esso è ortogonale alle superfici ad energia costante come appunto le linee di Fermi lungo le quali in definitiva si svolge il moto della elettrone. A seconda del verso di percorrenza si parla di orbita di tipo elettrone o di tipo lacuna. Si hanno orbite di tipo lacuna quando la cima di una banda piena possiede degli stati vuoti.
18) Lacune :
Fermo restando che gli unici portatori di carica sono gli elettroni ed hanno carica negativa, l´ipotesi della loro esistenza è molto utile per spiegare la seguente situazione :
Vi sia una banda completamente piena tranne che uno stato libero (lacuna) in cima ad essa, applicando un campo Ez nella direzione dei k crescenti si ha che gli elettroni (..e implicitamente la lacuna) si spostano a sinistra essendo ![]() . Considerando un istante successivo alla applicazione del campo si ha che la lacuna si è spostata, e la sua velocità è aumentata (..corrisponde alla tangente alla banda). Tale risultato può essere motivato o assegnando alla lacuna una carica negativa ed una massa negativa, oppure in accordo alla meccanica classica, una massa positiva ed una carica positiva.
. Considerando un istante successivo alla applicazione del campo si ha che la lacuna si è spostata, e la sua velocità è aumentata (..corrisponde alla tangente alla banda). Tale risultato può essere motivato o assegnando alla lacuna una carica negativa ed una massa negativa, oppure in accordo alla meccanica classica, una massa positiva ed una carica positiva.
19) Seconda legge della dinamica per gli elettroni liberi :
Si parte dalla determinazione del lavoro compiuto dal campo E su di un elettrone nel tempo dt ![]() inoltre
inoltre ![]() e quindi uguagliando i de si ha
e quindi uguagliando i de si ha  quindi è apparentemente rispettata la 2ª legge della dinamica, apparentemente in quanto k non è l´impulso della elettrone di Block dato che non rispetta la
quindi è apparentemente rispettata la 2ª legge della dinamica, apparentemente in quanto k non è l´impulso della elettrone di Block dato che non rispetta la ![]() .
.
20) Massa efficace :
È una misura della inerzia che un elettrone di Block presenta quando ad esso è applicata una forza esterna, si ricava derivando rispetto al tempo la vg si ha : ![]() e quindi si ha
e quindi si ha  dove m* è la massa efficace che quindi è inversamente proporzionale alla curvatura della curva di dispersione nello spazio dei k , in particolare in corrispondenza al bordo di zona la curvatura è negativa quindi lo è anche la massa efficace, il che vuol dire che applicando una forza diretta verso il bordo di zona, il moto avviene in senso opposto, ciò avviene per via della riflessione alla Bragg. In maniera analoga se ci si avvicina al bordo di zona dalla banda superiore la curvatura è positiva e con essa la massa efficace, che è piccola quindi è come se un effetto di rinculo agevola l´elettrone ad allontanarsi dal bordo di zona.
dove m* è la massa efficace che quindi è inversamente proporzionale alla curvatura della curva di dispersione nello spazio dei k , in particolare in corrispondenza al bordo di zona la curvatura è negativa quindi lo è anche la massa efficace, il che vuol dire che applicando una forza diretta verso il bordo di zona, il moto avviene in senso opposto, ciò avviene per via della riflessione alla Bragg. In maniera analoga se ci si avvicina al bordo di zona dalla banda superiore la curvatura è positiva e con essa la massa efficace, che è piccola quindi è come se un effetto di rinculo agevola l´elettrone ad allontanarsi dal bordo di zona.
21) Resistività di un metallo :
La resistività r di un metallo è funzione sia della temperatura che delle imperfezioni del reticolo, in particolare è da imputare a quest´ultime la resistività residua r0 che si ha anche quando la temperatura scende a 0 K. Si ha che la resistività parte dal valore r0 cresce come T5 per T << qD per poi crescere come T a temperature T << qD .
È importante comunque notare che per un metallo la resistività cresce al crescere della temperatura mentre per un semiconduttore la resistività diminuisce al crescere della temperatura.
22) Spiegazione della andamento lineare della resistività alle alte temperature :
Occorre far riferimento alla sfera di Fermi traslata ed alle modalità per riportarla nella posizione iniziale una volta che il campo elettrico non agisce più. La resistività aumenta per via degli urti di tipo Umklapp dei fononi con gli elettroni, i fononi utili sono quelli con k simile al kDebye ed il loro numero aumenta linearmente con la temperatura e con esso la resistività.
23) Spiegazione della andamento di tipo T5 della resistività in funzione della temperatura :
Col decrescere della temperatura, si osserva dalla funzione di Bose-Einstein che il numero dei fononi capaci di dar luogo ad urti di tipo Umklapp decresce in maniera esponenziale, però diviene significativo il numero dei fononi che a seguito di successivi urti con k più piccoli riescono ad ottenere lo stesso risultato.
