Linee di trasmissione

1) Collegamento unifilare :

Viene utilizzato un solo conduttore mentre per il ritorno si utilizza la terra.

 

2) Circuito a costanti distribuite :

Si parla di circuito a costanti distribuite quando il rapporto tra la lunghezza della linea e la velocità della luce è circa dello stesso ordine di grandezza delle variazioni temporali considerate significative. Se invece le variazioni temporali sono molto più lente, è sufficiente la analisi tramite il circuito a costanti concentrate.

 

3) Equazioni generali delle linee :

Assemblando le impedenze longitudinali in una unica impedenza ad unità di lunghezza e le ammettenze trasversali in una unica ammettenza ad unità di lunghezza  si può scrivere   da cui   , ed analogamente   da cui   .

 

4) Soluzione delle equazioni generali delle linee :

Derivando rispetto da x la  si ottiene  , ponendo la soluzione di questa equazione è . Analogamente derivando rispetto ad x la  si ottiene  la cui soluzione è  la quale può anche essere scritta in funzione di  semplicemente sostituendo nella  , si ha infatti    nella quale uguagliando i coefficienti degli esponenziali omologhi si ha    ed analogamente si trova

 dove Z₀ è detta impedenza caratteristica della linea. Pertanto le soluzioni delle equazioni delle linee sono :

                          

 

5) Costante di propagazione della linea :

 

6) Impedenza caratteristica :

 

7) Linea adattata :

Si tratta di una linea chiusa su di una impedenza pari alla sua impedenza caratteristica, la condizione di chiusura sul carico è quindi   sostituendo in essa le equazioni      e      si ottiene    e quindi   , sfruttando quest´ultima (…che sostanzialmente indica la assenza della onda regressiva) e la condizione di chiusura all´ingresso sul generatore, si ha   , in definitiva le equazioni nel caso di linea adattata sul carico sono   e   . Analogamente se il generatore V_g viene posto alla fine della linea ed il carico Z₀ all´inizio, si ha che  e quindi si ha soltanto l´onda regressiva.

 

8) Impedenza nel caso di linea adattata :

Quando la linea è adattata l´impedenza che si vede verso il carico in un qualsiasi punto della linea stessa è sempre uguale all´impedenza caratteristica. Si dimostra osservando che nel caso di onda progressiva il rapporto 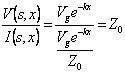 è costante, se invece consideriamo la linea adattata in ingresso si ha –Z₀ .

 

9) Soluzione delle equazioni delle linee nel caso di linea disadattata :

Il caso più generico possibile vede la linea chiusa all´ingresso su di un generatore V_g avente impedenza interna Z_g ¹ Z_o e chiusa in uscita su di una impedenza Z_u ¹ Z₀ . La condizione sul carico è pertanto   , sostituendo in essa le equazioni di V(s,x) e di I(s,x) si ottiene  dove  è l´impedenza di carico normalizzata, si ottiene pertanto 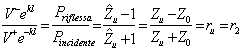 tale rapporto è denominato coefficiente di riflessione sul carico e consente di scrivere in forma compatta   . La condizione di chiusura sul generatore è invece  ossia, definendo  l´impedenza del generatore normalizzata,  da cui sostituendo  si ottiene  nella quale raccogliendo  e definendo il coefficiente di riflessione sul generatore 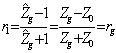 si ottiene 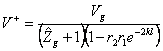che sostituita insieme a  nella   restituisce .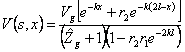

Linee ordinarie in regime transitorio

10) Linea LC :

È una linea per la quale si suppone siano nulle le perdite longitudinali (R) e trasversali (G) con questa semplificazione si ottiene   quindi nel caso di linea adattata si ha    antitrasformando si ha   pertanto si vede che la v(t,x) in un punto x della linea è pari alla v_g , ma solo dopo un tempo   detto tempo di transito, la velocità di fase si ottiene differenziando ed uguagliando a 0 la argomento della v_g cioè      Þ     .

 

11) Linea non distorcente e condizione di Heaviside :

Raccogliendo L e C nella costante di propagazione si ha 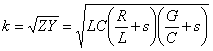  nella quale si può portare s fuori radice agevolando la antitrasformazione a patto che   ottenendo   e quindi nel caso di linea adattata si ha   la cui antitrasformata è      dalla quale si vede che il segnale è sia ritardato che attenuato.

 

12) Pupinizzazione e suoi problemi :

Nella pratica la conduttanza G è molto bassa, allora si ha  pertanto per avvicinarsi alla condizione di Heaviside si ricorre alla pupinizzazione che consiste nell´inserire delle induttanze concentrate lungo la linea allo scopo di aumentare l´induttanza distribuita della stessa, il problema è che così facendo si creano dei filtri passa-basso pertanto la linea ha una banda passante molto ridotta.

 

13) Linea RC :

Una linea RC è una linea per la quale si suppongono trascurabili G ed L, si ottiene . L'antitrasformata che ne consegue è in generale difficile, tranne nel caso in cui in ingresso alla linea si abbia un impulso, in tal caso infatti si ottiene una campana che è tanto più ampia quanto più ci si allontana dalla sorgente lungo la linea, il che impedisce di trasmettere segnali impulsivi a frequenza elevata su questo tipo di linea.

 

14) Approssimazione di una linea generica :

Una qualsiasi linea può essere pensata come una serie di una linea LC e di una linea RC.

 

15) Impedenza normalizzata sul generatore e sul carico :

                                                         

 

16) Coefficiente di riflessione sul generatore e sul carico :

                                                            

 

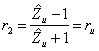
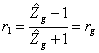
17) Comportamento di una linea adattata sul generatore e disadattata sul carico :

Si applica la relazione generale trovata per le linee disadattate 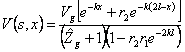 osservando che   e che 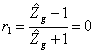 in accordo al fatto che se il generatore è adattato non si ha riflessione su di esso. In definitiva si ottiene   e considerando il centro  di una linea LC per la quale si ha   si può scrivere   essendo t il tempo di transito della linea LC ed analogamente   pertanto si ottiene  quindi si avrà che al tempo t/2 arriva nel punto centrale della linea il segnale erogato dal generatore al tempo t=0 mentre al tempo 1,5t arriva nel punto centrale della linea il segnale che ha subito una riflessione sul carico.

 

18) Comportamento di una linea disadattata sul generatore e disadattata sul carico :

Si applica la relazione generale trovata per le linee disadattate 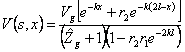 osservando che occorre calcolare tutte le grandezze e che il termine   può essere sviluppato in serie di Taylor.

Con considerazioni analoghe alle precedenti si ottiene il valore di v(t,x) nel punto centrale della linea che risulta essere somma delle continue riflessioni che ci sono sia sul carico che sul generatore. Abbiamo visto 3 casi :

a)       linea chiusa sul carico su di una impedenza doppia della Z₀ , chiusa in ingresso su di un generatore impulsivo avente impedenza pari alla metà della Z₀ ,  si ottengono una serie di impulsi.

b)       linea chiusa sul carico su di una impedenza doppia della Z₀ , chiusa in ingresso su di un generatore a gradino avente impedenza pari alla metà della Z₀,  si ottiene una serie di gradini di ampiezza sempre più piccola e che converge ad un valore finito.

c)       linea aperta sul carico, chiusa in ingresso su di un generatore a gradino privo di resistenza interna, si ottiene una serie di impulsi.

d)       linea aperta sul carico, chiusa in ingresso su di un generatore impulsivo privo di resistenza interna, si ha che in risposta ad un gradino si ottiene una forma d´onda periodica.

Linee in regime permanente

19) Costante di propagazione in regime permanente :

K=a(w)+jb(w)

Con a = costante di attenuazione della linea e   b = costante di fase.

 

20) Impedenza caratteristica in regime permanente :

Z = R₀(w) + jX₀(w)

 

21) Equazione delle linee in regime permanente :

Si possono sostituire i fasori nelle equazioni che avevamo trovato nel dominio di Laplace

                                              

L´espressione nel tempo di v(t,x) si ottiene ricordando che essa equivale alla parte reale del fasore rotante ossia

  

si nota quindi la presenza di un´onda progressiva e di un´onda regressiva, imponendo che la argomento del coseno sia costante (…uguagliando a 0 il differenziale) si trova la velocità di fase   per l´onda progressiva e   per l´onda regressiva.

 

22) Valore del coefficiente di riflessione all'ascissa x della linea  :

 

23) Carta di Smith :

Consente di determinare l'impedenza normalizzata in un punto x della linea, infatti tramite la  si può calcolare il coefficiente di riflessione in x essendo 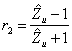 con  e quindi si ha 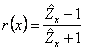. Quest'ultima è una relazione tra numeri complessi che associa al piano complesso delle impedenze normalizzate un punto del piano complesso dei coefficienti di riflessione.

 

24) Significato delle circonferenze della carta di Smith :

Le circonferenze che hanno il centro sull'asse immaginario positivo sono quelle che hanno .

Le circonferenze che hanno il centro sull'asse immaginario negativo sono quelle che hanno .

Le circonferenze che hanno il centro sull'asse reale sono quelle che hanno  , tra queste la massima circonferenza è quella che prevede resistenza 0, all´interno ci sono i valori della resistenza positivi, all´esterno ci dovrebbero essere i valori negativi ma ciò non ha senso in quanto la linea è passiva.

 

25) Punti salienti della carta di Smith :

(-2,0)  Þ corrisponde a  ossia ad un corto circuito, il coefficiente di riflessione è r = -1 .

(-1,0)  Þ corrisponde a  ossia all'adattamento, il coefficiente di riflessione è r = 0 .

( 0,0)  Þ corrisponde a  ossia ad un circuito aperto, il coefficiente di riflessione è r = 1 .

26) Andamento del coefficiente di riflessione in funzione della distanza dal carico per una linea LC e per una linea RC :

Linea LC :              per una linea LC si ha  k = a+jb = jb =  quindi il coefficiente di riflessione è   dove il 1° esponenziale è costante quindi si ha che r(x) è un vettore di modulo costante che ruota in senso antiorario se ci si sposta verso il carico (…x crescente) mentre ruota in senso antiorario se ci si sposta verso il generatore; è inoltre una funzione periodica con periodo .

Linea RC :             per una linea RC si ha  k = a + quindi il coefficiente di riflessione è  pertanto andando verso il generatore si ruota in senso orario e diminuisce il modulo secondo un andamento spiraleggiante in accordo con il concetto che una linea infinitamente lunga si autoadatta.

 

27) Rapporto d´onda stazionaria r :

La tensione lungo la linea è  che può anche essere scritta in funzione del coefficiente di riflessione sul carico r₂ infatti raccogliando  si ha 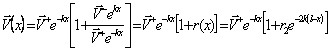. Osservando che i coefficienti di riflessione sono tutti compresi tra 0 ed 1, l'origine per essi si può prendere nel centro della carta di Smith dove si ha l'adattamento e quindi il coefficiente di riflessione deve valer 0. In tal modo si può quindi avere una espressione grafica di  e determinarne il valore massimo  ed il valore minimo definendo in tal modo l'importante parametro  .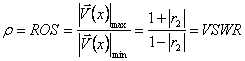

In particolare si ha che se la linea è adattata ROS=1 mentre se è disadattata ROS=¥ e questo come conseguenza del fatto che il coefficiente di riflessione sul carico può assumere solo valori compresi tra 0 ed 1 essendo il rapporto tra l'onda incidente e l'onda riflessa.

 

28) Matrice delle impedenze per il tronco di linea :

Il tronco di linea è un pezzetto di linea il quale è assimilabile ad una rete 2 porte simmetrica e reciproca, pertanto della sua matrice delle impedenze è sufficiente calcolare 2 termini su 4. Ricordando le note equazioni

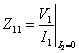Calcoliamo Z₁₁ e Z₂₁  ponendo I₂ = 0 ossia lasciando aperto il tronco di linea e mettendo al suo ingresso un generatore di corrente di valore impresso I₁ e applicando le relazioni delle linee. Sfruttando le condizioni di chiusura sul generatore e sul carico si ricavano i coefficienti V⁺ e V^- delle equazioni delle linee. Si ha  da cui si ottiene   mentre   da cui si ottiene . Per calcolare   e 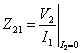     occorrono V₁  e V₂ , si ha  mentre .  Sostituendo i valori trovati si ottiene Z₁₁ e Z₂₁ e pertanto si può scrivere la seguente matrice delle impedenze 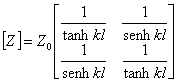  da cui per passare alla matrice delle ammettenze si debbono cambiare i segni ai termini sulla diagonale secondaria e dividere per il determinante che vale in questo caso .