Caratterizzazione esterna dei circuiti

1) Come valutare il tempo impiegato da un segnale per attraversare un circuito e relazione col ritardo di gruppo e di fase:

Effettuando una modulazione di ampiezza si riesce a marcare un segnale e quindi a valutare il tempo che impiega ad attraversare un circuito 2 porte. In particolare occorre inviare in ingresso il segnale  e considerare che la generica funzione di rete di una rete 2 porte è un n° complesso  pertanto    E quindi antitrasformando si ha una traslazione nel tempo  e sfruttando gli sviluppi in serie di Taylor arrestati al 1° ordine per     e      ed essendo Dw®0 si ottiene  nella quale il 2° coseno ha un argomento più lento del primo quindi individua l´inviluppo, il ritardo di gruppo è               mentre il primo coseno individua il ritardo di fase   .

 

2) Considerazioni riguardanti il circuito risonante parallelo ed il coefficiente di risonanza Q :

Alimentando il circuito RLC parallelo con un generatore di corrente I_g e valutando come uscita I_r si ha :

  Þ  

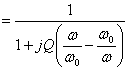    avendo posto    e   .

L´effetto della risonanza è ben visibile se si considera il modulo del rapporto 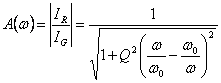    il quale tende ad 1 per w = w₀ e la cui forma d´onda è una gaussiana la cui ampiezza massima è sempre 1.

Per un circuito RLC  parallelo si ha    dalla quale si vede che Q aumenta se la resistenza è alta, ma questo può accadere solo se L e C sono di ottima fattura, tali cioè da non presentare resistenze parassite le quali poste in parallelo ad R sono in grado di abbassarne il valore e con esso il  Q.

 

3) Larghezza di banda :

È l´intervallo di frequenze per le quali la grandezza è inferiore per non più di  rispetto al valore massimo che viene assunto in corrispondenza alla risonanza.

 

4) Relazione tra il Q di un circuito risonante e la larghezza di banda :

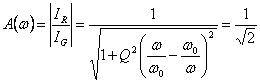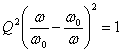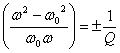La relazione   è verificata soltanto se  Û             Û               Û        

allora    .

 

5) Porta :

Si tratta di una coppia di morsetti tali che la corrente entrante in uno è uguale in modulo alla corrente uscente dalla altro.

 

6) Teorema di sostituzione :

In una rete qualsiasi una sua porzione, accessibile da una porta può essere sostituita con un generatore indipendente di tensione o di corrente, avente come grandezza impressa la corrispondente grandezza elettrica di porta. Se la rete restante si presenta come un generatore, il bipolo che si deve connettere è un generatore indipendente del tipo opposto.

 

7) Teorema di Thevenin :

Una rete accessibile da una porta è equivalente esternamente alla porta, alla rete stessa in cui le eccitazioni sono state disattivate con in serie alla porta un generatore di tensione avente tensione impressa uguale alla tensione che si manifesta a vuoto in corrispondenza alla porta della rete e con la stessa polarità.

Si dimostra sostituendo la rete a destra con un generatore di corrente ed applicando il teorema di sovrapposizione degli effetti per calcolare la V_AB alla porta. Quando si apre il generatore di corrente V_AB = V₀ , quando si disattiva la rete V_AB=I(rete disattivata).

 

8) Come applicare Thevenin se lo schema interno alla rete non è noto :

a)       si misura la V_AB lasciando la rete aperta.

b)       Si chiude la rete su di una resistenza variabile di cui si cambia il valore sino ad avere ai suoi capi , si è a tal punto raggiunto la adattamento e l´impedenza della rete è pari all´impedenza del carico.

 

9) Teorema di Norton :

Una rete accessibile da una porta è equivalente esternamente alla porta, alla rete stessa in cui le eccitazioni sono state disattivate con in parallelo alla porta un generatore di corrente avente corrente impressa uguale alla corrente di corto circuito della porta.

Si dimostra come Thevenin ma applicando un generatore di tensione.

 

10) Teorema del massimo trasferimento di potenza attiva :

Un bipolo Z_u alimentato da un generatore di tensione di impedenza interna Z_g assorbe da questo la massima potenza attiva quando la sua impedenza vale Z_g^* .

Si ha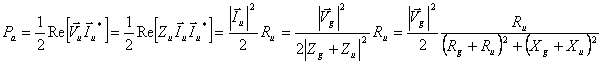  

Il termine  abbassa la potenza quindi ci serve che sia nullo cioè  si ottiene quindi 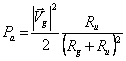 che assume il suo massimo per R_u = R_g quindi in definitiva la potenza è massima se .

In tal caso si ha però distorsione del segnale, pertanto per avere la massima potenza attiva mantenendo un segnale non distorto, l´impedenza di carico e l´impedenza del circuito debbono essere uguali ed entrambe reali.

 

11) Onda incidente ed onda riflessa su di un bipolo, coefficiente di riflessione :

È possibile scrivere 2 grandezze relative ad un bipolo come combinazione lineare di v ed i cioè    con opportuna scelta dei coefficienti si ha 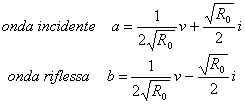     da cui invertendo si ha                             ed                             dove R₀ è una costante di normalizzazione.

Il coefficiente di riflessione è   .

 

12) Legame tra il coefficiente di riflessione r ed il massimo trasferimento di potenza attiva :

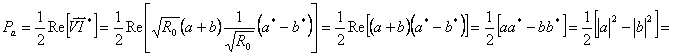
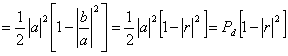    Si vede quindi che la potenza attiva è massima e coincide con la potenza disponibile quando il coefficiente di riflessione è 0 ossia Z_u = R₀ .

 

13) Rete 2 porte :

Si tratta di un circuito accessibile da 2 porte e privo di eccitazioni al suo interno.

 

14) Come ottenere i coefficienti della matrice impedenze a vuoto [ Z ] :

Questa matrice soddisfa la relazione 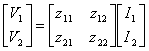  quindi in essa le variabili indipendenti sono le correnti, si può applicare il principio della sovrapposizione degli effetti costruendo 2 circuiti equivalenti che consentono ciascuno di calcolare 2 grandezze della matrice, in particolare ponendo un generatore di corrente I₁ all´ingresso della rete 2 porte e lasciando aperta la porta d´uscita quindi I₂=0 si possono rilevare i valori di V₁ e V₂ e quindi Z₁₁ e Z₂₂ , mentre ponendo un generatore di corrente I₂ all´uscita e lasciando aperto l´ingresso si calcolano le altre 2 grandezze del circuito.

 

15) Come ottenere i coefficienti della matrice ammettenze a vuoto [ Y ] :

Questa matrice soddisfa la relazione   quindi in essa le variabili indipendenti sono le tensioni, si può applicare il principio della sovrapposizione degli effetti costruendo 2 circuiti equivalenti che consentono ciascuno di calcolare 2 grandezze della matrice, in particolare ponendo un generatore di tensione V₁ all´ingresso della rete 2 porte e cortocircuitando la porta d´uscita quindi V₂=0 si possono rilevare i valori di I₁ e I₂ e quindi Y₁₁ e Y₂₂ , mentre ponendo un generatore di tensione V₂ all´uscita e cortocircuitando l´ingresso si calcolano le altre 2 grandezze del circuito.

 

16) Come ottenere i coefficienti della matrice ibrida a vuoto [ H ] :

Questa matrice soddisfa la relazione 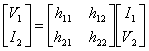  quindi in essa le variabili indipendenti sono la corrente d´ingresso e la tensione d´uscita, si può applicare il principio della sovrapposizione degli effetti costruendo 2 circuiti equivalenti che consentono ciascuno di calcolare 2 grandezze della matrice, in particolare ponendo un generatore di corrente I₁ all´ingresso della rete 2 porte e cortocircuitando la porta d´uscita quindi V₂=0 si possono rilevare i valori di V₁ e I₂ e quindi h₁₁ e h₂₂ , mentre ponendo un generatore di tensione V₂ all´uscita e aprendo l´ingresso si calcolano le altre 2 grandezze del circuito.

 

17) Come ottenere i coefficienti della matrice ibrida inversa a vuoto [ G ] :

Questa matrice soddisfa la relazione  quindi in essa le variabili indipendenti sono la corrente d´uscita e la tensione d´ingresso, si può applicare il principio della sovrapposizione degli effetti costruendo 2 circuiti equivalenti che consentono ciascuno di calcolare 2 grandezze della matrice, in particolare ponendo un generatore di tensione V₁ all´ingresso della rete 2 porte e aprendo la porta d´uscita quindi I₂=0 si possono rilevare i valori di I₁ e V₂ e quindi g₁₁ e g₂₂ , mentre ponendo un generatore di corrente I₂ all´uscita e cortocircuitando l´ingresso si calcolano le altre 2 grandezze del circuito.

 

18) Come ottenere i coefficienti della matrice di trasmissione [ T ] :

Questa matrice soddisfa la relazione 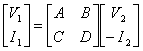  quindi in essa le variabili indipendenti sono sulla stessa porta il che rende necessario l´utilizzo del nullore per calcolarne i coefficienti, in particolare si può applicare il principio della sovrapposizione degli effetti costruendo 2 circuiti equivalenti che consentono ciascuno di calcolare 2 grandezze della matrice, infatti ponendo un generatore di tensione V₂ all´uscita della rete 2 porte ed in serie ad esso un nullatore, si ha che I₂ =0 e si possono quindi rilevare i valori di I₁ e V₁ e da essi calcolare A e C , mentre ponendo un generatore di corrente I₂ all´uscita ed in parallelo ad esso un nullatore, si ha che V₂ = 0 e si possono quindi rilevare i valori di I₁ e V₁ e da essi calcolare B e D. In entrambe i casi sulla porta d´ingresso si ha un noratore in modo che tensione e corrente sulla stessa possono variare liberamente.

 

19) Condizione da rispettare per la connessione di reti 2 porte :

Quando si uniscono delle reti 2 porte, deve sempre essere rispettata la condizione per la quale nelle reti 2 porte costituenti, la corrente entrante nel morsetto di una porta deve essere sempre uguale alla corrente uscente dalla altro morsetto della stessa porta.

20) Impedenza della serie di 2 reti 2 porte :

Vale la consueta relazione delle serie  , si dimostra osservando che la corrente entrante nella 1ª porta della rete A è uguale alla corrente entrante nella 1ª porta della rete B mentre la tensione applicata in ingresso alle due reti è la somma delle tensioni applicate singolarmente, si ha :

 

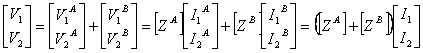
21) Prove di validità nel caso di connessione serie-serie :

In base al teorema di sostituzione si può mettere un generatore di corrente sia in ingresso che in uscita dalla rete e considerare separatamente l'effetto dei due generatori applicando la sovrapposizione degli effetti

Si deve verificare che la corrente che scorre nel ramo comune alle 2 uscite sia nulla quando il circuito d´uscita della rete globale è aperto e quindi non scorre in esso corrente mentre in ingresso è applicato un generatore di corrente. Analogamente si deve verificare che la corrente che scorre nel ramo comune ai 2 ingressi sia nulla quando il circuito d´ingresso della rete globale è aperto e quindi non vi scorre corrente, mentre in uscita è applicato un generatore di corrente. La prova è sempre verificata se si pone un trasformatore in uscita da una delle 2 porte perché in tal modo si impone di comportarsi correttamente alla porta che è chiusa sul primario, l'altra porta della stessa rete deve fare altrettanto e così facendo si ha lo stesso anche per la 1ª porta della rete B e conseguentemente per la seconda.

 

22) Ammettenza del parallelo di 2 reti 2 porte :

Vale la consueta relazione dei paralleli  , si ricava osservando che le tensioni applicate in ingresso alla singola porta sono uguali mentre la corrente è la somma delle correnti , si ha :

 

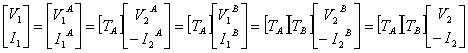
23) Prove di validità nel caso di connessione parallelo – parallelo :

Si deve verificare che sia nulla la corrente che scorre tra le uscite delle reti 2 porte componenti quando si cortocircuitano le uscite della rete globale e si pone un generatore di tensione in ingresso ad essa. Analogamente si deve verificare che sia nulla la corrente che scorre tra gli ingressi delle reti 2 porte componenti quando si cortocircuitano gli ingressi della rete globale e si pone un generatore di tensione in uscita ad essa. La prova è sempre verificata se si pone in cascata ad una delle 2 reti un trasformatore ideale con rapporto di trasformazione unitario.

 

24) Matrice di trasmissione di una cascata di 2 reti 2-porte :

 

Si dimostra procedendo dall´ingresso verso l´uscita utilizzando la matrice T per ogni rete 2 porte, si ha :

 

25) Circuito equivalente :

Si ottiene dalle relazioni che danno luogo alla matrice corrispondente (impedenze, ammettenze, …) associando ai termini misti dei generatori controllati, ed ai termini omogenei delle impedenze o delle trasmittenze.

 

26) Rete 2-porte reciproca :

È una rete per la quale se consideriamo 2 situazioni diverse (1) e (2) , le grandezze elettriche alle porte rispettano la seguente uguaglianza :                                               

Essendo  la tensione alla porta d´ingresso nella situazione 1 e la corrente alla porta d´uscita nella situazione 2.

 

27) Rete 2-porte simmetrica :

È una rete per la quale si possono scambiare vicendevolmente la porta d´ingresso e la porta d´uscita senza provocare conseguenze esterne alla rete stessa.

 

28) Relazione tra simmetria e reciprocità :

La simmetria implica la reciprocità ma non è vero che una rete reciproca debba necessariamente essere simmetrica.

 

29) Dimostrare che ogni bipolo è reciproco :

Si deve dimostrare che date 2 situazioni elettriche diverse, è rispettata la relazione di Lorentz  ma si ha   ed anche       allora si ottiene   che è sicuramente una uguaglianza.

 

30) Relazione tra una rete 2 porte costituita da bipoli e la reciprocità :

Una rete 2 porte costituita da bipoli comunque connessi è reciproca. Si dimostra chiudendo la rete 2 porte su 2 generatori di corrente, questo si può fare in virtù del teorema di sostituzione, è chiaro quindi che le grandezze di porta coincideranno con le grandezze impresse. Applicando Tallegen sono valide le 2 relazioni 

                        

Ma le due sommatorie sono uguali perché ogni bipolo preso singolarmente è reciproco quindi si ottiene    che è proprio la condizione di reciprocità di Lorentz.

 

31) Conseguenze della reciprocità sulla rappresentazione delle reti 2 porte :

Per la [Z] si ha Z₁₂ = Z₂₁ mentre per la [T] si ha determinante unitario, tali condizioni si possono determinare a partire dalle diverse situazioni operative che consentono il calcolo dei parametri di una data matrice, e sostituendole nella condizione di Lorentz.

 

32) Conseguenze della simmetria sulla rappresentazione delle reti 2 porte :

Per la [Z] gli elementi sulle diagonali sono uguali tra di loro mentre per la [T] si ha determinante unitario e A = D.

 

33) Matrice delle impedenze per una rete a “T” :

                                   dove Z_C è l´impedenza posta in parallelo.

34) Matrice delle ammettenze per una rete a “p” :

                                           dove Y₁ e Y₂ sono le impedenze poste in parallelo.

 

35) Matrice delle ammettenze per una rete 2-porte a “T derivato” :

La rete può essere vista come parallelo di 2 reti, una a “T” ed una costituita da una sola resistenza che connette l´ingresso con l´uscita, la matrice ammettenza risultante è la somma delle matrici ammettenza di queste 2 reti.

 

36) Matrice delle ammettenze per una rete 2-porte a “doppio T” :

La rete può essere vista come parallelo di 2 reti a “T” , quindi la matrice ammettenza risultante è la somma delle matrici ammettenze di queste 2 reti.

 

37) Parametri immagine :

Si tratta di 4 parametri (2 impedenze immagini Z_i1 e Z_i2 e 2 esponenti di trasduzione su base immagine g₁₂ e g₂₁) i quali sotto opportune condizioni consentono di valutare semplicemente il comportamento di una rete costituita da una cascata di più reti.

38) Impedenze immagini :

L´impedenza che si vede in ingresso ad una rete 2-porte chiusa su di una impedenza Z_u è funzione sia di Z_u che della rete 2 porte, in particolare utilizzando le equazioni della matrice [Z] e la condizione di chiusura  e si trova   ed analogamente se si chiude l´ingresso su Z_U , l´impedenza vista dalla porta d´uscita è  .                L´impedenza immagine Z_i1 è tale che quando chiudiamo la porta 2 su Z_i2 si ha Z_i1 =z_i1 e quando chiudiamo la porta 1 su Z_i1 si ha Z_i2 =z_i2 .

39) Chiusura su base immagine :

Una cascata di reti 2 porte si dice chiusa su base immagine quando ogni rete componente vede alla sua sinistra la propria impedenza immagine Z_i1 ed alla propria destra la analoga Z_i2 .

 

40) Esponente di trasduzione su base immagine ingresso-uscita :

Descrive il trasferimento del segnale , si suppone che la rete 2 porte sia eccitata in modo qualsiasi alla porta d´ingresso e chiusa sull´impedenza immagine Z_i2 , si ha :               

 

41) Esponente di trasduzione su base immagine uscita-ingresso :

Descrive il trasferimento del segnale , si suppone che la rete 2 porte sia eccitata in modo qualsiasi alla porta d´uscita e chiusa sull´impedenza immagine Z_i1 , si ha :          

 

42) Proprietà di una cascata di reti 2 porte su base immagine :

a)       Le impedenze immagine Z_i1 di ognuna coincidono con l´impedenza immagine della prima porta e le impedenze immagine Z_i2 coincidono con l´impedenza immagine della ultima porta.

b)       Gli esponenti di trasduzione sono pari alla somma dei rispettivi esponenti di trasduzione delle singole reti costituenti.