Proprietà dei sistemi nello spazio di stato
1) Norma di una matrice :
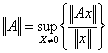
essendo definita in termini della norma di x è evidente che diverse scelte per la ||x|| comportano differenti norme di A.
2) Equilibrio di un sistema di equazioni differenziali :
Assumendo che il sistema ![]() ammetta la soluzione banale x = 0 questa viene assunta come equilibrio e si assume che la soluzione relativa al punto iniziale x0 esista in un suo intorno.
ammetta la soluzione banale x = 0 questa viene assunta come equilibrio e si assume che la soluzione relativa al punto iniziale x0 esista in un suo intorno.
3) Equilibrio stabile :
L'equilibrio è detto essere stabile se per ogni e >0 esiste un d>0 tale che ![]() per ogni t³t0 e a patto che ||x0|| < d . In sostanza si ha che se il punto iniziale x0 è contenuto in una ipersfera di raggio d centrata in t0 allora si ha che la soluzione del sistema di equazioni differenziali rimane confinata in un ipercilindro di raggio e attorno all'asse t il che comporta che se l'equilibrio è stabile in corrispondenza al tempo t=t0 allora è stabile in corrispondenza a qualsiasi tempo iniziale t1 > t0 pur di scegliere un opportuno valore per d.
per ogni t³t0 e a patto che ||x0|| < d . In sostanza si ha che se il punto iniziale x0 è contenuto in una ipersfera di raggio d centrata in t0 allora si ha che la soluzione del sistema di equazioni differenziali rimane confinata in un ipercilindro di raggio e attorno all'asse t il che comporta che se l'equilibrio è stabile in corrispondenza al tempo t=t0 allora è stabile in corrispondenza a qualsiasi tempo iniziale t1 > t0 pur di scegliere un opportuno valore per d.
4) Equilibrio attrattivo :
L´equilibrio risulta essere attrattivo se esiste h>0 tale che si ha ![]() per ogni ||x0|| < h .
per ogni ||x0|| < h .
5) Equilibrio asintoticamente stabile :
L´equilibrio è detto asintoticamente stabile se è contemporaneamente sia stabile che attrattivo.
6) Equilibrio asintoticamente stabile globale :
Si tratta del caso in cui come valore iniziale si prenda un punto diverso dall´origine.
7) Equilibrio instabile :
L´equilibrio della equazione differenziale ![]() è instabile se non è stabile.
è instabile se non è stabile.
8) Condizioni di equilibrio per un sistema lineare e stazionario :
La soluzione dell'equazione di stato nel caso stazionario è ![]() considerando inizialmente assenza di forzamento quindi
considerando inizialmente assenza di forzamento quindi ![]() si osserva che la soluzione è combinazione lineare di termini
si osserva che la soluzione è combinazione lineare di termini ![]() dove li è l'autovalore della matrice dinamica ed r la sua molteplicità, si ha pertanto che l´equilibrio è asintoticamente stabile se tutte le radici del polinomio caratteristico della matrice A hanno parte reale negativa, se anche una sola di esse è a parte reale positiva, l´equilibrio è instabile.
dove li è l'autovalore della matrice dinamica ed r la sua molteplicità, si ha pertanto che l´equilibrio è asintoticamente stabile se tutte le radici del polinomio caratteristico della matrice A hanno parte reale negativa, se anche una sola di esse è a parte reale positiva, l´equilibrio è instabile.
Nel caso invece che vi siano radici a parte reale nulla aventi molteplicità 1 allora, relativamente ad esse, il sistema è stabile ma non asintoticamente stabile mentre il sistema è instabile se le radici a parte reale nulla hanno molteplicità maggiore di uno.
Considerando anche la risposta forzata, si ha che il sistema risulta stabile se gli autovalori della matrice dinamica sono tutti a parte reale negativa ed il forzamento è limitato infatti ![]() .
.
9) Stato controllabile :
Uno stato è detto essere controllabile in corrispondenza ad un tempo t>0 se esiste una funzione di ingresso u ammissibile tale che si abbia ![]() lo spazio degli stati controllabili è indicato con Xc.
lo spazio degli stati controllabili è indicato con Xc.
10) Matrice di controllabilità :
![]()
essa consente di individuare all'interno dello spazio di stato il sottospazio degli stati controllabili determinato appunto dall'immagine di questa matrice.
11) Caratteristica fondamentale della insieme degli stati controllabili :
L´insieme degli stati controllabili non dipende dal tempo t, questo soltanto in via teorica in quanto per un sistema fisico reale, passare da uno stato non nullo ad uno stato nullo in un tempo arbitrario potrebbe richiedere un ingresso talmente ampio da mandare in saturazione qualche elemento del sistema.
12) Sistema controllabile :
È un sistema per il quale l´insieme degli stati controllabili coincide con lo spazio di stato, ciò accade se la matrice di controllabilità ha rango massimo, ossia è invertibile.
13) Sistema raggiungibile :
Un sistema è detto essere raggiungibile se assumendo che lo stato iniziale sia nullo x(0) = 0 , si può far in modo di raggiungere un determinato stato finale xf al tempo t applicando un opportuno ingresso tra 0 e t.
14) Forma di Kalman per la controllabilità :
Se il rango della matrice di controllabilità non è massimo, e quindi lo spazio degli stati controllabili è più piccolo dello spazio di stato, occorre scegliere come base per lo spazio di stato una base i cui primi vettori siano una base per lo spazio degli stati controllabili ed i restanti vettori siano qualsiasi purchè in numero opportuno.
Nella nuova base il sistema è descritto dalle matrici 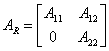 ;
; ![]() ;
; ![]() , inoltre il vettore di stato può essere partizionato in un vettore
, inoltre il vettore di stato può essere partizionato in un vettore ![]() relativo agli stati controllabili ed un vettore
relativo agli stati controllabili ed un vettore ![]() relativo agli stati non controllabili, si possono agevolmente estrinsecare le equazioni di stato e da esse dedurre lo schema a blocchi equivalente. La funzione di trasferimento che si ricava
relativo agli stati non controllabili, si possono agevolmente estrinsecare le equazioni di stato e da esse dedurre lo schema a blocchi equivalente. La funzione di trasferimento che si ricava ![]() è relativa solo al sottosistema controllabile descritto da A11 , b1 , c1 .
è relativa solo al sottosistema controllabile descritto da A11 , b1 , c1 .
15) Forma di Jordan per la controllabilità :
Se la matrice dinamica A è diagonalizzabile, allora il sistema è controllabile a patto che le componenti del vettore d´ingresso trasformato nella nuova base siano tutte non nulle. Se invece A non è diagonalizzabile, allora occorre trasformarla nella forma canonica di Jordan e la condizione di controllabilità è che le componenti del vettore d´ingresso trasformato bi corrispondenti alle ultime righe dei blocchi di Jordan che costituiscono la matrice trasformata siano non nulle.
16) Stato indistinguibile dallo stato 0 :
Uno stato x è indistinguibile dallo stato 0 nell´intervallo (0,t) se vale la relazione ![]() con
con ![]() , ossia se allo stato corrisponde una risposta in evoluzione libera nulla nell´intervallo (0,t).
, ossia se allo stato corrisponde una risposta in evoluzione libera nulla nell´intervallo (0,t).
17) Stati non osservabili :
Uno stato è non osservabile se è indistinguibile dallo stato 0. Lo spazio degli stati non osservabili è indicato con Xno.
18) Matrice di osservabilità :
È la matrice 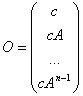 , essa consente di individuare all'interno dello spazio di stato il sottospazio degli stati non osservabili determinato appunto dal nucleo di questa matrice.
, essa consente di individuare all'interno dello spazio di stato il sottospazio degli stati non osservabili determinato appunto dal nucleo di questa matrice.
19) Sistema osservabile :
Un sistema è osservabile se l´insieme degli stati non osservabili ha dimensione nulla pertanto non esistono stati inosservabili diversi da zero, ciò accade se la matrice di osservabilità ha il rango massimo ossia il nucleo (…che individua gli stati non osservabili) coincide con l'insieme vuoto.
20) Forma di Kalman per l´osservabilità :
Se il nucleo della matrice di osservabilità non ha dimensione nulla, occorre scegliere come base per lo spazio di stato una base i cui primi vettori siano una base per lo spazio degli stati non osservabili ed i restanti vettori siano qualsiasi purchè in numero opportuno. Nella nuova base il sistema è descritto dalle matrici :
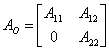 ;
; 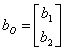 ;
; ![]()
inoltre il vettore di stato può essere partizionato in un vettore ![]() relativo agli stati non osservabili ed un vettore
relativo agli stati non osservabili ed un vettore ![]() relativo agli stati osservabili , si possono agevolmente estrinsecare le equazioni di stato e da esse dedurre lo schema a blocchi equivalente. La funzione di trasferimento che si ricava
relativo agli stati osservabili , si possono agevolmente estrinsecare le equazioni di stato e da esse dedurre lo schema a blocchi equivalente. La funzione di trasferimento che si ricava ![]() è relativa solo al sottosistema osservabile descritto da A22 , b2 , c2 .
è relativa solo al sottosistema osservabile descritto da A22 , b2 , c2 .
21) Forma di Jordan per l´osservabilità :
Se la matrice dinamica A è diagonalizzabile, allora il sistema è osservabile a patto che le componenti del vettore d´uscita trasformato nella nuova base siano tutte non nulle. Se invece A non è diagonalizzabile, allora occorre trasformarla nella forma canonica di Jordan e la condizione di osservabilità è che le componenti del vettore d´uscita trasformato cj corrispondenti alle prime righe dei blocchi di Jordan che costituiscono la matrice trasformata siano non nulle.
22) Decomposizione canonica di Kalman :
Occorre determinare 4 basi :
a) B1 è una base per gli stati controllabili e non osservabili
b) B2 è un completamento di B1 ad una base per lo spazio degli stati controllabili
c) B3 è un completamento di B1 ad una base per lo spazio degli stati non osservabili
d) B4 è un completamento di B1 È B2 È B3 ad una base di Â4
nella base di Ân che si ottiene giustapponendo i vettori delle precedenti basi, il sistema è descritto dalle matrici :
 ;
; 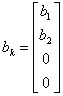 ;
; ![]()
inoltre il vettore di stato può essere partizionato in :
un vettore x1(t) riferito al sistema controllabile
un vettore x2(t) riferito al sistema controllabile e osservabile
un vettore x3(t) riferito al sistema non controllabile e non osservabile
un vettore x4(t) riferito al sistema non controllabile e osservabile
Un risultato importante è che la funzione di trasferimento che si ricava ![]() è relativa solo al sottosistema controllabile ed osservabile.
è relativa solo al sottosistema controllabile ed osservabile.
23) Condizione affinchè un sistema sia osservabile e controllabile :
Esso deve essere scritto in forma minima ossia la funzione di trasferimento non deve avere cancellazioni.
24) Cancellazioni lecite :
Una cancellazione è detta lecita se il modo ad essa associato è stabile.
25) Realizzazione :
S´intende il passaggio dalla rappresentazione mediante la funzione di trasferimento a quella nello spazio di stato.
26) Realizzazione in forma canonica di controllore :
Si tratta del passaggio dalla funzione di trasferimento alla matrice di controllabilità.
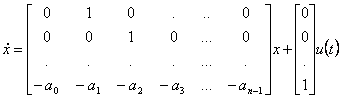
![]()
dove i b0 …bm sono i coefficienti del numeratore della funzione di trasferimento e gli a0 …an-1 sono i coefficienti del denominatore monico della stessa. La matrice di controllabilità di questo sistema risulta essere di rango massimo indipendentemente dal fatto che ci siano state o meno cancellazioni e quindi il sistema è sicuramente controllabile.
27) Realizzazione in forma canonica di osservatore :
Si tratta del passaggio dalla funzione di trasferimento alla matrice di osservabilità
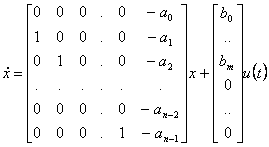
![]()
dove i b0 …bm sono i coefficienti del numeratore della funzione di trasferimento e gli a0 …an-1 sono i coefficienti del denominatore monico della stessa. La matrice di osservabilità di questo sistema risulta essere di rango massimo indipendentemente dal fatto che ci siano state o meno cancellazioni e quindi il sistema è sicuramente osservabile.
28) Realizzazione in forma canonica di Jordan :
Si tratta del passaggio dalla funzione di trasferimento alla forma di Jordan, esso è particolarmente utile nel caso che il denominatore della funzione di trasferimento sia facilmente fattorizzabile, e quindi si possano calcolare i residui, si può impostare il problema in due modi diversi ottenendo risultati uguali solo per quel che riguarda la matrice dinamica A.
Ad esempio considerando un polo triplo e due poli semplici le equazioni di stato associate sono :
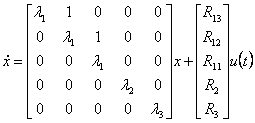
![]()
