La funzione di trasferimento

1) Risposta in evoluzione libera :

È la risposta del sistema quando sono ad esso applicate le condizioni iniziali e nessun segnale d´ingresso.

 

2) Risposta in evoluzione forzata :

È la risposta del sistema quando è ad esso applicato il solo segnale d´ingresso, senza le condizioni iniziali.

 

3) Sistema causale :

Si tratta di un sistema nel quale la risposta non precede l´eccitazione, oppure analogamente il sistema è causale se a 2 ingressi uguali in un certo intervallo di tempo risponde con 2 uscite uguali nello stesso intervallo di tempo.

 

4) Ingressi canonici :

Gli ingressi canonici sono quelli che consentono di sottoporre ad un test completo un sistema, in quanto questo presenta una risposta diversa a seconda del segnale con il quale viene eccitato.

 

5) Gradino unitario :

Si ottiene come limite per e®0  della integrale della d(t,e) ossia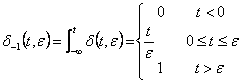               

esso vale     .

 

6) Ingresso canonico fondamentale :

Si tratta della impulso matematico fondamentale o d di Dirac esso è definito come limite per e ® 0 della funzione 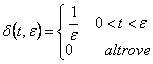                                               e vale                                    

si può ottenere anche per derivazione della d_-1(t).

 

7) Proprietà della d di Dirac :

                   se     t > 0

                                  se     t > 0

8) Rampa di ordine k :

Si ottiene come limite per e®0  della integrale k_esimo della d(t,e) ossia 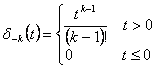             scritta in questo modo è verificata la relazione    .

9) Considerazioni sulle funzioni sinusoidali utilizzate come ingressi canonici :

Esse possono essere sviluppate in serie di potenze le quali non sono altro che combinazioni lineari di ingressi di tipo a rampa di ordine crescente i quali sono ingressi canonici e quindi lo sono anche le funzioni sinusoidali.

 

10) Relazione tra la forma cartesiana del numero complesso e la forma polare :

La forma cartesiana è   mentre la forma polare è  , tali rappresentazioni coincidono se si considera il valore principale dell'argomento ossia -p < j < p   ed i piani hanno la stessa origine.

 

11) Trasformata di Laplace :

La trasformata della funzione f(t) è data dall´integrale indefinito .

 

12) Condizioni sufficienti affinché una funzione f(t) ammetta trasformata di Laplace :

a)    f(t) deve essere continua a tratti per t > 0.

b)    " t₀ finito deve esistere M₁ tale che |f(t)| < M₁    con 0 < t < t₀ .

c)    f(t) deve essere di ordine esponenziale per t®¥  cioè deve esistere M₂ e s₀ ed un t₀ tale che  per t>t₀ . Dove s₀ è detta ascissa di convergenza in quanto l´integrale di Laplace è convergente per ogni s tale che          Re s > s₀  .

 

13) Proprietà della traslazione nel tempo :

è anche detto teorema del ritardo.

 

14) Proprietà della traslazione nel dominio di s :

si noti che quando la traslazione è nel dominio di s i segni sono discordi.

 

15) Proprietà del cambiamento della scala temporale :

Si osservi che ad una contrazione nel dominio del tempo corrisponde una espansione nel dominio di Laplace.

 

16) Proprietà della derivazione reale :

    mentre per la derivata seconda si ha 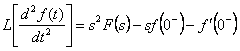. Nelle applicazioni le condizioni iniziali sono nulle e quindi la trasformata della derivata n_esima vale .

 

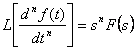17) Proprietà della integrazione reale :

 

18) Proprietà della derivazione complessa :

 

19) Proprietà della integrazione complessa :

 

20) Teorema del valore finale :

È un teorema che consente di conoscere la risposta a regime (t®¥) di un sistema valido nell´ipotesi che sF(s) sia analitica (esiste sia la funzione che le sue derivate) sulla asse immaginario e nel semipiano destro del piano s.  

In pratica la analiticità della sF(s) si ha se essa non presenta poli con parte reale positiva o nulla.

 

21) Teorema del valore iniziale :

                                               non ci sono in questo caso condizioni su sF(s).

 

22) Teorema della convoluzione reale o della moltiplicazione complessa :

La convoluzione reale è data dal prodotto sotto integrale tra una funzione ed una seconda funzione che trasla, esso è pari alla moltiplicazione complessa ossia nel dominio della s, si ha : 

 

23) Antitrasformata di Laplace :

Essa è data dal seguente integrale di Bromwich   .

 

24) Funzione di trasferimento :

È il rapporto tra la trasformata della risposta in evoluzione forzata (condizioni iniziali nulle) e la trasformata della ingresso applicato, si tratta sempre di funzioni razionali fratte a meno che non siano presenti dei ritardi che non possono essere trascurati, nel qual caso si hanno delle funzioni trascendenti.

 

25) Equazione caratteristica :

È l´equazione che si ottiene eguagliando a 0 il denominatore Q(s) della funzione di trasferimento dove il termine in s di grado massimo ha coefficiente 1.

 

26) Residui associati ad una coppia di poli complessi coniugati :

Sono 2 numeri complessi coniugati pertanto sfruttando le formule di Eulero danno luogo ad una evoluzione nel tempo di tipo sinusoidale.

 

27) Antitrasformata associata ad una coppia di poli complessi coniugati :

Sia il polo s_i +jw_i ed il residuo in forma polare Me^jj allora si ha   .

 

28) Costante di tempo t associata ad un polo reale :

Una volta scomposta la funzione di trasferimento in fratti semplici, per il polo reale si ha 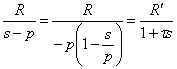      con          e     =  costante di tempo.

 

29) Coefficiente di smorzamento x :

È il seno della angolo compreso tra il semiasse immaginario positivo ed il segmento che unisce il polo con l´origine  dove s_i è la parte reale del numero complesso e w_ni il suo modulo.

 

30) Pulsazione naturale w_ni :

Si tratta del modulo del n° complesso s + jw  che individua il polo

31) Pulsazione di risonanza w_i :

Corrisponde alla parte immaginaria del polo, è desumibile anche dal modulo del coefficiente di smorzamento

 

32) Scomposizione in fratti semplici di un polo multiplo :

Se n è l´ordine del polo si scrivono n termini i quali hanno tutti come base (s-p) elevato ad una potenza che per ogni fratto cresce di 1 sino ad arrivare ad n. Il coefficiente di quest´ultimo si calcola come per i poli semplici, mentre il coefficiente del termine di grado precedente si calcola derivando la parte analitica e dividendo per il fattoriale pari all´ordine della derivata, analogamente per gli altri fratti via via decrescenti sino ad arrivare al fratto avente  il denominatore di grado 1, solo il relativo coefficiente a numeratore può essere chiamato residuo. La formula per determinare tali coefficienti è pertanto 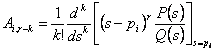   mentre nell'antitrasformazione di fratti aventi denominatore con grado maggiore di 1 si utilizza la formula  .

 

33) Valutazione grafica del valore del residuo relativo al polo j_esimo :

Si utilizza la formula    dove i vettori   e    hanno tutti la punta entrante nel polo j_esimo e   q e y  sono gli angoli da essi formati con il riferimento orizzontale.