L'analisi nello spazio di stato
1) Variabili di stato :
Sono le variabili che si debbono creare quando si ha una equazione differenziale di ordine n e la si vuole ridurre ad un sistema di n equazioni differenziali di 1° grado, si tratta quindi di variabili intermedie le quali non necessariamente corrispondono a grandezze fisicamente misurabili tuttavia consentono una descrizione del sistema più accurata rispetto alla funzione di trasferimento. Esse costituiscono un vettore di stato se si può ottenere il valore della uscita in un tempo
t > t0 noto che sia il valore di tutte le variabili di stato al tempo t0 ed il valore degli ingressi ui al tempo t ³ t0 .
2) Confronto tra la approccio mediante la variabile di stato e la approccio mediante la funzione di trasferimento :
L´approccio mediante la funzione di trasferimento è valido solo nel caso di sistema lineare e stazionario preferibilmente ad un solo ingresso ed una sola uscita mentre la approccio mediante le variabili di stato essendo impostato nel dominio del tempo, non ha queste limitazioni.
3) Spazio di stato :
È lo spazio nel quale i componenti del vettore di stato sono gli assi coordinati.
4) Traiettoria di stato :
È il percorso descritto, nello spazio di stato, dall´estremo libero del vettore di stato al variare del tempo.
5) Equazioni dinamiche per un sistema MIMO :
Un sistema MIMO possiede diversi ingressi e diverse uscite è descritto dal sistema ![]() dove :
dove :
A è la matrice di sistema, o matrice dinamica
B è la matrice d´ingresso al sistema, o matrice di forzamento
C è la matrice d´uscita dal sistema
D è la matrice di connessione diretta ingresso uscita, nei sistemi reali essa è nulla
u è il vettore di ingresso
y è il vettore di uscita
x è il vettore di stato
6) Equazioni di stato per un sistema SISO :
Un sistema SISO possiede un solo ingresso ed una sola uscita, è descritto dal sistema ![]() dove stavolta b, u e c sono vettori e non matrici come si aveva nei sistemi MIMO.
dove stavolta b, u e c sono vettori e non matrici come si aveva nei sistemi MIMO.
7) Equazioni di stato del motore in corrente continua controllato sull'armatura :
Osservando le equazioni ![]() ,
, ![]() ,
, ![]() ,
, ![]() , si osserva che le uniche grandezze derivate sono im(t) eed wm(t) pertanto si prestano bene a costituire il vettore di stato, del resto inoltre la variabile d'ingresso di un motore in corrente continua alimentato sull'armatura è senz'altro la tensione di alimentazione dell'armatura ea(t) mentre la variabile d'uscita è senz'altro la velocità angolare wm(t). Isolando
, si osserva che le uniche grandezze derivate sono im(t) eed wm(t) pertanto si prestano bene a costituire il vettore di stato, del resto inoltre la variabile d'ingresso di un motore in corrente continua alimentato sull'armatura è senz'altro la tensione di alimentazione dell'armatura ea(t) mentre la variabile d'uscita è senz'altro la velocità angolare wm(t). Isolando ![]() al primo membro della 4ª equazione e sostituendo in essa la 2ª ed anche isolando
al primo membro della 4ª equazione e sostituendo in essa la 2ª ed anche isolando ![]() al 1° membro della 3ª equazione e sostiutendo in essa la 1ª si perviene alle seguenti equazioni di stato
al 1° membro della 3ª equazione e sostiutendo in essa la 1ª si perviene alle seguenti equazioni di stato 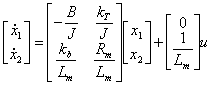
![]() dove x1 = wm x2 = im u = ea y = wm .
dove x1 = wm x2 = im u = ea y = wm .
8) Matrice di transizione dello stato nel caso di ingresso nullo :
È una matrice che in assenza di forzamento consente di passare dal vettore di stato al tempo 0 al vettore di stato al tempo t ossia ![]() , la sua espressione si ottiene risolvendo mediante Laplace l'equazione differenziale
, la sua espressione si ottiene risolvendo mediante Laplace l'equazione differenziale ![]() e poi antitrasformandola, si ha infatti
e poi antitrasformandola, si ha infatti ![]() e quindi
e quindi ![]() da cui antitrasformando si ha
da cui antitrasformando si ha ![]() e quindi si ha che la matrice di transizione dello stato è
e quindi si ha che la matrice di transizione dello stato è ![]() . Si può dimostrare che essa è esprimibile anche in forma di esponenziale di matrice
. Si può dimostrare che essa è esprimibile anche in forma di esponenziale di matrice ![]() .
.
9) Proprietà della esponenziale di matrice :
a) ![]()
b) ![]()
c) ![]()
10) Proprietà della matrice di transizione dello stato :
a) ![]()
b) ![]()
c) ![]()
11) Equazione di transizione dello stato :
Trasformando secondo Laplace la ![]() si ha
si ha ![]() e quindi
e quindi ![]() , antitrasformando quest'ultima si ha
, antitrasformando quest'ultima si ha ![]() e ricordando che
e ricordando che ![]() e che al prodotto nel domio di Laplace corrisponde la convoluzione nel domio del tempo si ha
e che al prodotto nel domio di Laplace corrisponde la convoluzione nel domio del tempo si ha ![]() , da essa si può ricavare la risposta del sistema che risulta essere la somma della risposta libera e della risposta forzata
, da essa si può ricavare la risposta del sistema che risulta essere la somma della risposta libera e della risposta forzata
![]()
12) Equazione di transizione dello stato a partire da un tempo iniziale qualsiasi t0 :
![]()
13) Risposta a regime yr(t) :
È la risposta che si ha per t®¥ ovvero per t0®-¥ ossia ![]() .
.
14) Risposta transitoria yt(t) :
![]()
dove 2 integrali sono stati ridotti ad uno cambiando opportunamente gli estremi di integrazione.
15) Calcolo degli autovalori di una matrice A :
Si debbono trovare le soluzioni dell'equazione caratteristica ![]() .
.
16) Dimensioni del nucleo della matrice A :
![]()
dove n è la dimensione della matrice e r(A) il rango ossia il numero di righe o di colonne indipendenti. Questa relazione applicata ad (A-lI) consente di valutare immediatamente la molteplicità geometrica per un dato autovalore e quindi vedere se la matrice a cui appartiene può essere diagonalizzata o meno.
17) Calcolo degli autovettori di una matrice A :
Dopo aver trovato gli autovalori, li si sostituisce uno alla volta nella matrice (A-lI) , si avrà necessariamente che una riga si annulla e quindi uguagliando a zero si individua il nucleo come span di uno o più vettori, in particolare nel caso che la molteplicità algebrica sia r, allora la molteplicità geometrica, cioè il numero dei corrispondenti autovettori, è compreso tra 1 ed r, la matrice risulta diagonalizzabile solo se la molteplicità geometrica è r.
18) Inversa di una matrice T :
Si ha ![]() dove l'aggiunta ha nella posizione ( riga r , colonna c) il determinante della sottomatrice che si ottiene eliminando la colonna r e la riga c , il tutto pesato con la matrice dei segni alternati.
dove l'aggiunta ha nella posizione ( riga r , colonna c) il determinante della sottomatrice che si ottiene eliminando la colonna r e la riga c , il tutto pesato con la matrice dei segni alternati.
19) Metodi per il calcolo della matrice di transizione dello stato j(t) = eAt :
a) Si può individuare una matrice T di cambiamento di base costituita dagli autovettori della matrice A che la trasformi in una matrice L sulla cui diagonale sono presenti gli autovalori di A i quali vanno moltiplicati per t ed elevati ad e, ottenendo in tal modo la matrice diagonale eLt , infine si ritorna nella base di partenza ![]() .
.
b) Si deve antitrasformare secondo Laplace la matrice (sI – A)-1 .
20) Forma canonica di Jordan :
Le matrici che non possono essere diagonalizzate in quanto posseggono autovalori la cui molteplicità algebrica è diversa dalla molteplicità geometrica, possono comunque essere portate ad una forma "quasi diagonale" detta forma canonica di Jordan nella quale vi sono ovunque zeri tranne che sulla diagonale principale dove vi sono i blocchi di Jordan ciascuno dei quali ha sulla diagonale l'autovalore multiplo e sulla diagonale immediatamente sopra tutti 1.
21) Numero di blocchi di Jordan associati ad ogni autovalore :
È pari alla differenza tra la dimensione n della matrice A ed il rango della matrice (A-l1I) o, più semplicemente, è pari alla molteplicità geometrica dell'autovalore.
22) Autovettore generalizzato di ordine k :
Si tratta di un autovettore il quale rispetta le seguenti 2 proprietà :
a) (A- l1I)kvk = 0
b) (A- l1I)k-1vk ¹ 0
23) Procedura per il calcolo di eAt tramite la forma canonica di Jordan :
a) si trovano gli autovalori della matrice A
b) si calcolano gli autovettori per gli autovalori aventi molteplicità algebrica pari alla molteplicità geometrica
c) per ciascuno degli altri autovalori si calcolano gli autovettori generalizzati con la seguente procedura
1) si individua il numero di catene di autovettori e quindi di blocchi di Jordan associati al singolo autovalore, tale numero è pari alla molteplicità geometrica dell'autovalore che si può valutare come differenza tra le dimensioni della matrice A ed il rango della matrice (A-lI)
2) si calcola la lunghezza di una delle catene associate all'autovalore multiplo calcolando (A-lI)i con i = 1,2,3,… sinchè il rango della matrice ottenuta al passo k+1 è uguale al rango della matrice ottenuta al passo k, la lunghezza della catena è pertanto k
3) ricordando le relazioni che definiscono l'autovettore generalizzato (A- l1I)kvk = 0 e (A- l1I)k-1vk ¹ 0 si calcola il vettore uk appartenente al nucleo di (A-lI)k e tramite le relazioni
vk-1 = (A- l1I)vk , vk-2 = (A- l1I)vk-1 , …. , v1 = (A- l1I)v2 si ottengono ricorsivamente gli altri autovettori appartenenti alla catena
4) se al punto 2) si è rilevata la presenza di un'altra catena, ne è nota implicitamente la lunghezza k e quindi si trova l'altro autovettore di ordine k appartenente al nucleo della matrice (A-lI)k e da esso si ottengono poi ricorsivamente gli altri autovettori.
d) si riuniscono tutti gli autovettori trovati in una matrice T che porta nella forma di Jordan
e) si calcola eJt ricordando che ad ogni blocco di Jordan presente sulla diagonale è associato un blocco siffatto : 
f) si calcola eAt = T eJt T-1 .
24) Come passare dall´equazione di stato alla funzione di trasferimento :
Le trasformate di Laplace delle equazioni di stato sono ![]() e
e ![]() in quest'ultima il 1° termine a 2° membro è zero in quanto per la funzione di trasferimento si considerano le condizioni iniziali nulle x(0) = 0 , si ha quindi
in quest'ultima il 1° termine a 2° membro è zero in quanto per la funzione di trasferimento si considerano le condizioni iniziali nulle x(0) = 0 , si ha quindi ![]() e quindi
e quindi 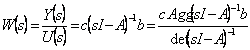 si vede quindi come i poli della funzione di trasferimento coincidono con gli autovalori della matrice dinamica A.
si vede quindi come i poli della funzione di trasferimento coincidono con gli autovalori della matrice dinamica A.
