Riflessione e rifrazione delle onde piane
1) Incidenza normale su un materiale dielettrico :
In questo caso ![]() , per rispettare le condizioni di continuità dei componenti tangenziali dei campi E ed H si genera un'onda riflessa ed un'onda rifratta pertanto le equazioni sono
, per rispettare le condizioni di continuità dei componenti tangenziali dei campi E ed H si genera un'onda riflessa ed un'onda rifratta pertanto le equazioni sono ![]() e
e ![]() , proiettandole sugli assi si ottiene
, proiettandole sugli assi si ottiene ![]() ed anche
ed anche ![]() , sostituendo la 1ª nella 2ª si individua il rapporto
, sostituendo la 1ª nella 2ª si individua il rapporto ![]() detto coefficiente di riflessione per incidenza normale, analogamente si giunge al coefficiente di riflessione per il campo H
detto coefficiente di riflessione per incidenza normale, analogamente si giunge al coefficiente di riflessione per il campo H ![]() , si osserva che se il campo E è concorde, il campo H è discorde e viceversa. I coefficienti di trasmissione sono
, si osserva che se il campo E è concorde, il campo H è discorde e viceversa. I coefficienti di trasmissione sono ![]() e
e ![]() .
.
2) Incidenza normale su un materiale dissipativo :
Abbiamo visto che per un'onda piana che si propaga in un mezzo conduttore si ha ![]() mentre per l'onda che si propaga nel mezzo dielettrico è
mentre per l'onda che si propaga nel mezzo dielettrico è ![]() ed
ed ![]() quindi il coefficiente di riflessione è
quindi il coefficiente di riflessione è 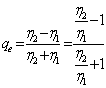 essendo
essendo ![]() per la presenza di g al denominatore che tende ad ¥ , si ha che qE @ 1 e con considerazioni analoghe
per la presenza di g al denominatore che tende ad ¥ , si ha che qE @ 1 e con considerazioni analoghe
qH @1 quindi il campo E rifratto sarà nullo mentre il campo H rifratto sarà il doppio di quello incidente ma decade esponenzialmente penetrando nel mezzo dissipativo mentre nel mezzo dielettrico si instaura un'onda stazionaria alla quale non è associato alcun trasporto di potenza.
3) Incidenza obliqua su un materiale dielettrico :
Supponiamo l'asse x orizzontale, l'asse y uscente dal foglio e l'asse z diretto verso il basso, pertanto supponendo che l'onda incidente appartenga al piano xz si ha che il vettore b ha componente sia lungo x che lungo z, per z=0 l'uguaglianza tra le componenti tangenziali di E porta alla relazione ![]() , uguaglianza che si ha per ogni terna di campi a patto che i 3 esponenziali siano uguali ossia che
, uguaglianza che si ha per ogni terna di campi a patto che i 3 esponenziali siano uguali ossia che ![]() da questa relazione deriva la legge di Erone
da questa relazione deriva la legge di Erone ![]() e la legge di Snell
e la legge di Snell ![]() nonché essendo
nonché essendo ![]() l'ovvia uguaglianza tra le velocità di fase lungo x delle 3 onde. Per determinare i coefficienti di riflessione si considerano due vettori E0h ed E0v locati nel piano ortogonale a b , E0h diretto lungo y (…uscente dal foglio) ed E0v nella direzione
l'ovvia uguaglianza tra le velocità di fase lungo x delle 3 onde. Per determinare i coefficienti di riflessione si considerano due vettori E0h ed E0v locati nel piano ortogonale a b , E0h diretto lungo y (…uscente dal foglio) ed E0v nella direzione ![]() , trattandosi di un'onda piana si ha
, trattandosi di un'onda piana si ha ![]() (…si osservi l'inversione dei versori) inoltre in maniera analoga si scrivono i campi E ed H relativi all'onda riflessa e all'onda rifratta. Proiettando E ed H lungo y si ottengono le relazioni
(…si osservi l'inversione dei versori) inoltre in maniera analoga si scrivono i campi E ed H relativi all'onda riflessa e all'onda rifratta. Proiettando E ed H lungo y si ottengono le relazioni ![]() e
e ![]() , sostituendo la 1ª nella 2ª si ottiene
, sostituendo la 1ª nella 2ª si ottiene ![]() la quale raccogliendo h2 ed utilizzando
la quale raccogliendo h2 ed utilizzando ![]() ,
, ![]() , porta alla
, porta alla 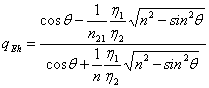 , si osserva che qEh cresce monotonamente dal calore che ha per incidenza normale sino al valore 1 assunto per incidenza tangente.
, si osserva che qEh cresce monotonamente dal calore che ha per incidenza normale sino al valore 1 assunto per incidenza tangente.
Proiettando E ed H lungo y si ottengono le relazioni ![]() ed
ed ![]() ricavando E0v si ottiene
ricavando E0v si ottiene ![]() che, con considerazioni analoghe a quelle fatte per qeh si riduce a
che, con considerazioni analoghe a quelle fatte per qeh si riduce a 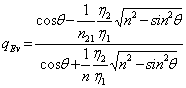 . Dalla prima espressione si nota che esiste anche un valore di q detto angolo di Brewster per il quale qEv si annulla, si deve avere
. Dalla prima espressione si nota che esiste anche un valore di q detto angolo di Brewster per il quale qEv si annulla, si deve avere ![]() che, elaborata porta alla
che, elaborata porta alla 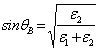 .
.
4) Incidenza obliqua su un materiale dissipativo :
I campi incidenti hanno la consueta espressione ![]() ,
, ![]() come pure i campi riflessi
come pure i campi riflessi ![]() ,
, ![]() mentre per i campi rifratti occorre tener conto che
mentre per i campi rifratti occorre tener conto che ![]() e quindi
e quindi ![]() ,
, ![]() . Per z =0 si deve avere la continuità delle componenti tangenziali dei campi e quindi l'uguaglianza degli esponenti la quale è verificata solo se
. Per z =0 si deve avere la continuità delle componenti tangenziali dei campi e quindi l'uguaglianza degli esponenti la quale è verificata solo se ![]() che uguagliando i coefficienti reali dà
che uguagliando i coefficienti reali dà ![]() e quindi nel mezzo dissipativo a è parallelo all'asse z mentre eguagliando i coefficienti immaginari si ha
e quindi nel mezzo dissipativo a è parallelo all'asse z mentre eguagliando i coefficienti immaginari si ha ![]() che è ancora la legge di Snell ma mostra che
che è ancora la legge di Snell ma mostra che ![]() non è parallelo a
non è parallelo a ![]() e quindi l'onda nel mezzo non dissipativo non è più uniforme. Dall'uguaglianza
e quindi l'onda nel mezzo non dissipativo non è più uniforme. Dall'uguaglianza ![]() si possono derivare una equazione relativa alla parte reale ed una equazione relativa alle parti immaginarie, da esse è possibile dedurre
si possono derivare una equazione relativa alla parte reale ed una equazione relativa alle parti immaginarie, da esse è possibile dedurre ![]() ed
ed ![]() sviluppando i seguenti casi :
sviluppando i seguenti casi :
a) Mezzo con bassa dissipazione :
![]() e
e ![]()
quindi il vettore di fase è lo stesso che si ha nel caso di mezzo non dissipativo mentre per il modulo del vettore di attenuazione si ha che è proporzionale alla conducibilità e dipende anche della angolo di incidenza.
b) Mezzo conduttore :
![]() e
e ![]()
analogamente a quanto si aveva nel caso di onde uniformi, il motivo di ciò è che l´onda rifratta si propaga quasi ortogonalmente alla superficie di discontinuità quindi a´ // b´ che è proprio la definizione di onda uniforme.
Viene inoltre definita la profondità di penetrazione ossia la distanza dalla superficie di discontinuità a cui il campo si riduce ad ![]() del suo valore iniziale per via della conducibilità, si ha
del suo valore iniziale per via della conducibilità, si ha 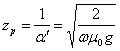 e si osserva come essa sia infinitesima per un conduttore ideale (…g®¥) , questo è il motivo per il quale i conduttori sono utilizzati come schermi elettromagnetici e lo spessore necessario diminuisce al crescere della frequenza.
e si osserva come essa sia infinitesima per un conduttore ideale (…g®¥) , questo è il motivo per il quale i conduttori sono utilizzati come schermi elettromagnetici e lo spessore necessario diminuisce al crescere della frequenza.
Per determinare i coefficienti di riflessione occorre tener conto che il 2° mezzo è dissipativo pertanto la relazione tra ![]() ed
ed ![]() è
è ![]() con
con ![]() dal rapporto tra E0 ed H0 si deduce l'impedenza d'onda superficiale
dal rapporto tra E0 ed H0 si deduce l'impedenza d'onda superficiale ![]() la quale solo per un conduttore coincide con l'impedenza intrinseca, il coefficiente di riflessione può essere scritto
la quale solo per un conduttore coincide con l'impedenza intrinseca, il coefficiente di riflessione può essere scritto 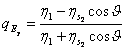 e si nota che la potenza incidente su un conduttore viene quasi completamente rifratta quindi la potenza da esso dissipata è infinitesima, pur essendo dissipativo.
e si nota che la potenza incidente su un conduttore viene quasi completamente rifratta quindi la potenza da esso dissipata è infinitesima, pur essendo dissipativo.
5) Riflessione totale :
L'angolo di rifrazione è 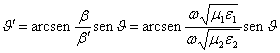 chiaramente se
chiaramente se ![]() (…cioè se la velocità di propagazione nel mezzo 1 è minore che non nel mezzo 2) si ha che esiste un angolo limite qL tale che
(…cioè se la velocità di propagazione nel mezzo 1 è minore che non nel mezzo 2) si ha che esiste un angolo limite qL tale che 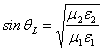 e quindi
e quindi ![]() ossia l'onda rifratta si propaga parallelamente alla superficie di discontinuità.
ossia l'onda rifratta si propaga parallelamente alla superficie di discontinuità.
Per qL si ha che ![]() è massimo quindi la velocità di fase dell'onda rifratta è minima ma sempre maggiore della velocità di fase lungo x dell'onda incidente in quanto si è supposto
è massimo quindi la velocità di fase dell'onda rifratta è minima ma sempre maggiore della velocità di fase lungo x dell'onda incidente in quanto si è supposto ![]() tuttavia se l'onda rifratta è non uniforme si ha che aumenta
tuttavia se l'onda rifratta è non uniforme si ha che aumenta ![]() e quindi diminuisce la velocità di fase dell'onda rifratta consentendo in tal modo l'uguaglianza richiesta dalle condizioni al contorno, in definitiva si ha che per q < qL l'onda rifratta è uniforme mentre per q > qL è non uniforme. Per quanto riguarda la potenza si ha che se polarizziamo orizzontalmente l'onda incidente, anche l'onda rifratta è polarizzata orizzontalmente ed il vettore di Poynting ha una componente immaginaria lungo z0 quindi non c'è trasporto di potenza attraverso la superficie di discontinuità ma solo parallelamente ad essa in quanto si ha anche una componente reale lungo x0 del vettore di Poynting.
e quindi diminuisce la velocità di fase dell'onda rifratta consentendo in tal modo l'uguaglianza richiesta dalle condizioni al contorno, in definitiva si ha che per q < qL l'onda rifratta è uniforme mentre per q > qL è non uniforme. Per quanto riguarda la potenza si ha che se polarizziamo orizzontalmente l'onda incidente, anche l'onda rifratta è polarizzata orizzontalmente ed il vettore di Poynting ha una componente immaginaria lungo z0 quindi non c'è trasporto di potenza attraverso la superficie di discontinuità ma solo parallelamente ad essa in quanto si ha anche una componente reale lungo x0 del vettore di Poynting.
