Propagazione
1) Equazione delle onde contenente il potenziale vettore magnetico per un mezzo disomogeneo :
Essendo H solenoidale ![]() , per esso esiste un potenziale vettore A tale che
, per esso esiste un potenziale vettore A tale che ![]() , sostituendolo nella
, sostituendolo nella ![]() si ottiene
si ottiene ![]() il quale sostituito insieme a
il quale sostituito insieme a ![]() nella
nella ![]() restituisce
restituisce ![]() avendo sfruttato la relazione
avendo sfruttato la relazione ![]() e definito la costante dielettrica equivalente
e definito la costante dielettrica equivalente ![]() . Sostituendo la condizione di Lorentz
. Sostituendo la condizione di Lorentz ![]() si ha al 1° membro
si ha al 1° membro ![]() e definendo
e definendo ![]() si ottiene
si ottiene ![]() .
.
dalla quale si nota che anche le disomogeneità dielettriche del mezzo si possono considerare come sorgenti elettriche.
2) Equazione delle onde contenente il potenziale vettore per un mezzo debolmente disomogeneo :
Nella ![]() il termine
il termine ![]() si può trascurare a patto che sia rispettata la condizione
si può trascurare a patto che sia rispettata la condizione 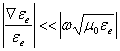 quindi nel caso di alte frequenze o di mezzo debolmente disomogeneo si ha
quindi nel caso di alte frequenze o di mezzo debolmente disomogeneo si ha ![]() .
.
3) Utilizzo del potenziale vettore :
L'equazione delle onde con il potenziale vettore viene utilizzata solo quando ci si trova in prossimità delle sorgenti in quanto all'esterno delle sorgenti vale la relazione omogenea ![]() del tutto simile a quella che si puà ottenere per il campo elettrico
del tutto simile a quella che si puà ottenere per il campo elettrico ![]() e per il campo magnetico
e per il campo magnetico ![]() .
.
4) Equazione eiconale ed equazione del trasporto :
L'equazione delle onde per un mezzo debolmente disomogeneo e non dissipativo è ![]()
dove ![]() ed
ed ![]() , per essa Luneburg Kline ipotizzano una soluzione nella forma
, per essa Luneburg Kline ipotizzano una soluzione nella forma ![]() la quale sostituita nell'equazione può individuare delle condizioni che debbono essere verificate, in particolare si osserva che E(r) è il prodotto di uno scalare
la quale sostituita nell'equazione può individuare delle condizioni che debbono essere verificate, in particolare si osserva che E(r) è il prodotto di uno scalare ![]() per un vettore
per un vettore ![]() e che il laplaciano del prodotto è
e che il laplaciano del prodotto è ![]() , sostituendo e semplificando si ottiene
, sostituendo e semplificando si ottiene ![]() .
.
Sviluppando la sommatoria ed eguagliando i coefficienti di k02 si ottiene l'equazione eiconale ![]() mentre eguagliando i coefficienti di k0 si ottiene l'equazione del trasporto
mentre eguagliando i coefficienti di k0 si ottiene l'equazione del trasporto ![]() .
.
5) Velocità di propagazione nella direzione r0 :
L'espressione del campo elettrico funzione dello spazio e del tempo che deriva dall'espansione asintotica di Luneburg & Kline è ![]() , ossia si tratta di una funzione sinusoidale sia del tempo che dello spazio, si ha che
, ossia si tratta di una funzione sinusoidale sia del tempo che dello spazio, si ha che ![]() al crescere di t se
al crescere di t se ![]() ossia considerando la direzione di propagazione r0 , si deve avere
ossia considerando la direzione di propagazione r0 , si deve avere ![]() da cui si ottiene la velocità di fase nella direzione di r0
da cui si ottiene la velocità di fase nella direzione di r0 ![]() .
.
6) Espressione dei campi E ed H in funzione della posizione :
Se si considera il mezzo poco disomogeneo, si può utilizzare l'espansione asintotica di Luneburg & Kline, in essa se w è sufficientemente elevata si possono considerare solo i termini dominanti E0 ed H0 ottenendo ![]() e
e ![]() , sostituendoli nella
, sostituendoli nella ![]() e sfruttando la relazione vettoriale
e sfruttando la relazione vettoriale ![]() si ottiene
si ottiene 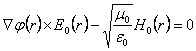 mentre sostituendo nella
mentre sostituendo nella ![]() si ottiene
si ottiene ![]() . Sostituendo in entrambe
. Sostituendo in entrambe ![]() ,derivante dall'equazione eiconale, e l'impedenza intrinseca del mezzo
,derivante dall'equazione eiconale, e l'impedenza intrinseca del mezzo ![]() si ottiene :
si ottiene :
![]()
![]()
dove s0 è il versore nella direzione di ![]() ossia è ortogonale alle superfici equifase.
ossia è ortogonale alle superfici equifase.
7) Impedenza intrinseca locale :
![]()
8) Raggi elettromagnetici :
Si tratta di curve che in ogni punto sono ortogonali alla superficie di propagazione, lungo di esse si propaga l'energia elettromagnetica, come si può osservare dal vettore di Poynting ![]() dove si è utilizzata la relazione vettoriale
dove si è utilizzata la relazione vettoriale ![]() ed essendo s0 il versore ortogonale alle superfici d'onda j(r) = costante. Le caratteristiche della traiettoria dei raggi possono essere desunte dall'equazione eiconale tramite la quale si ricava
ed essendo s0 il versore ortogonale alle superfici d'onda j(r) = costante. Le caratteristiche della traiettoria dei raggi possono essere desunte dall'equazione eiconale tramite la quale si ricava ![]() , relazione da cui si deduce che il raggio rimane confinato nel piano individuato da s0 e
, relazione da cui si deduce che il raggio rimane confinato nel piano individuato da s0 e ![]() ed ha curvatura
ed ha curvatura ![]() ossia ha la concavità rivolta verso la regione con indice di rifrazione crescente, ad esempio per l'atmosfera il raggio si incurva verso il basso in quanto più ci si avvicina alla terra, più aumenta la concentrazione e quindi l'indice di rifrazione.
ossia ha la concavità rivolta verso la regione con indice di rifrazione crescente, ad esempio per l'atmosfera il raggio si incurva verso il basso in quanto più ci si avvicina alla terra, più aumenta la concentrazione e quindi l'indice di rifrazione.
9) Legge di Snell generalizzata :
Dall'equazione eiconale si ottiene ![]() applicando il rotore e ricordando che rot grad[.] = 0 si ha
applicando il rotore e ricordando che rot grad[.] = 0 si ha ![]() cui si può applicare il teorema di Stokes ottenendo
cui si può applicare il teorema di Stokes ottenendo ![]() , scegliendo pertanto un circuito rettangolare in cui al lato superiore corrisponde un indice di rifrazione n ed al lato inferiore un indice di rifrazione n+dn , facendo tendere a zero i lati verticali si ottiene
, scegliendo pertanto un circuito rettangolare in cui al lato superiore corrisponde un indice di rifrazione n ed al lato inferiore un indice di rifrazione n+dn , facendo tendere a zero i lati verticali si ottiene ![]() dove q è l'angolo compreso tra s0 e la verticale discendente z0 .
dove q è l'angolo compreso tra s0 e la verticale discendente z0 .
10) Principio di Fermat:
Afferma che la lunghezza del percorso elettromagnetico ![]() è stazionaria ossia l´energia elettromagnetica si propaga lungo le traiettorie che rendono minimo il valore di L .
è stazionaria ossia l´energia elettromagnetica si propaga lungo le traiettorie che rendono minimo il valore di L .
11) Andamento dei raggi in un mezzo stratificato radialmente :
In un mezzo stratificato radialmente, l´indice di rifrazione ha simmetria radiale, si ottiene che il raggio rimane confinato in un piano passante per l´origine della struttura sferica e contenente s0 .
12) Andamento dei raggi in un mezzo stratificato piano :
Un mezzo stratificato piano è un mezzo per il quale l´indice di rifrazione varia solo con la quota z, dalla ![]() si deduce che il raggio rimane sempre confinato in un piano ortogonale al piano xy , si ottiene che se q è l'angolo compreso tra s0 e z0 , si ha
si deduce che il raggio rimane sempre confinato in un piano ortogonale al piano xy , si ottiene che se q è l'angolo compreso tra s0 e z0 , si ha ![]() .
.
13) Raggi nella troposfera :
Si tratta della parte bassa della atmosfera che va da 0 a 10km ai poli e da 0 a 15Km all´equatore, essa è costituita da Azoto (78.1%) , Ossigeno (20.9%) , vapor d´acqua sino ad un massimo del 5% ed altri gas. L'indice di rifrazione varia con la quota in funzione della densità e della polarizzabilità dei singoli componenti, al livello del mare vale 1,0003 , per valutarne le piccole variazioni viene definita la rifrattività ![]() che per l'atmosfera ad f £ 40GHz vale
che per l'atmosfera ad f £ 40GHz vale ![]() essendo pt la pressione atmosferica totale e pw la pressione parziale del vapor d´acqua e quindi il primo termine è il termine secco avente valori elevati ma stabili in quanto compresi tra 265N e 284N mentre il termine noto subisce forti variazioni potendo passare da 102N a 31N. Si osserva che la rifrattività diminuisce al crescere della quota h secondo la
essendo pt la pressione atmosferica totale e pw la pressione parziale del vapor d´acqua e quindi il primo termine è il termine secco avente valori elevati ma stabili in quanto compresi tra 265N e 284N mentre il termine noto subisce forti variazioni potendo passare da 102N a 31N. Si osserva che la rifrattività diminuisce al crescere della quota h secondo la ![]() dove Ns è il valore della rifrattività al suolo e h0 la altezza caratteristica che vale circa 8Km, questi valori in particolare variano con le condizioni metereologiche pertanto a bassa quota si ha :
dove Ns è il valore della rifrattività al suolo e h0 la altezza caratteristica che vale circa 8Km, questi valori in particolare variano con le condizioni metereologiche pertanto a bassa quota si ha :
a) atmosfera substandard se ![]() unità N/Km
unità N/Km
b) atmosfera standard se ![]() unità N/Km
unità N/Km
c) atmosfera superstandard se ![]() unità N/Km .
unità N/Km .
14) Raggio terrestre equivalente :
Nel caso di collegamenti tra stazioni situate a terra si ha che l'angolo q tra il versore s0 tangente al raggio elettromagnetico e ![]() diretto radialmente verso il basso è circa 90° pertanto la curvatura è
diretto radialmente verso il basso è circa 90° pertanto la curvatura è ![]() , considerando inoltre che la curvatura della terra è
, considerando inoltre che la curvatura della terra è ![]() si può fare un cambio di coordinate
si può fare un cambio di coordinate ![]() che annulla la curvatura del raggio elettromagnetico semplicemente a patto di ingrandire la terra. Inoltre essendo
che annulla la curvatura del raggio elettromagnetico semplicemente a patto di ingrandire la terra. Inoltre essendo ![]() si ha
si ha ![]() , si vede che se
, si vede che se ![]() allora Re®¥ e quindi l'energia si propaga parallelamente alla superficie terrestre, ossia si instaura un condotto elettromagnetico.
allora Re®¥ e quindi l'energia si propaga parallelamente alla superficie terrestre, ossia si instaura un condotto elettromagnetico.
15) Visibilità tra antenne :
Due antenne si dicono essere in visibilità quando il raggio elettromagnetico che le congiunge non interseca la superficie terrestre, dato che il raggio elettromagnetico presenta la concavità rivolta verso la terra si ha che la visibilità elettromagnetica è maggiore della visibilità geometrica.
16) Approssimazione WKB :
Sostituendo nell'equazione del trasporto ![]() la
la ![]() che si ricava dalla eiconale si ottiene
che si ricava dalla eiconale si ottiene ![]() nella quale :
nella quale :
a) considerando un versore t0 ortogonale ad s0 si può scomporre il gradiente in queste due direzioni e quindi scrivere ![]()
b) ![]()
c) per la definizione di divergenza, considerando un tubo di flusso avente sezione iniziale S, si ha ![]() .
.
Sostituendo si ottiene ![]() che moltiplicata per E0* e semplificata restituisce
che moltiplicata per E0* e semplificata restituisce 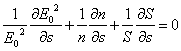 ossia dei termini che scaturiscono dalla derivata di un logaritmo, in definitiva si ha
ossia dei termini che scaturiscono dalla derivata di un logaritmo, in definitiva si ha 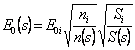 mentre per il termine di fase dell'espansione di Luneburg & Kline si ha
mentre per il termine di fase dell'espansione di Luneburg & Kline si ha ![]() , l'approssimazione WKB determina il valore del campo all'ascissa curvilinea s
, l'approssimazione WKB determina il valore del campo all'ascissa curvilinea s ![]() .
.
17) Andamento del campo in un mezzo dissipativo debolmente disomogeneo :
L'equazione eiconale ![]() essendo
essendo ![]() con
con ![]() (…tiene quindi conto sia delle dissipazioni dovute alla conducibilità che di quelle dovute alla polarizzazione), non è soddisfatta a meno che la funzione di fase non sia una funzione complessa
(…tiene quindi conto sia delle dissipazioni dovute alla conducibilità che di quelle dovute alla polarizzazione), non è soddisfatta a meno che la funzione di fase non sia una funzione complessa ![]() , sostituendo tale espressione nell'eiconale ed eguagliando le parti reali si ottiene
, sostituendo tale espressione nell'eiconale ed eguagliando le parti reali si ottiene ![]() mentre eguagliando le parti immaginarie si ha
mentre eguagliando le parti immaginarie si ha ![]() dove
dove ![]() è ortogonale alle superfici equiampiezza, l'espressione del campo diviene
è ortogonale alle superfici equiampiezza, l'espressione del campo diviene ![]() .
.
18) Andamento del campo in un mezzo debolmente disomogeneo e debolmente dissipativo :
Un mezzo è debolmente dissipativo se 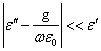 ossia se pur rimanendo complesso l'indice di rifrazione, si ha che la parte reale prevale nettamente sulla parte immaginaria, si ottiene che le superfici equifase e le superfici equiampiezza coincidono,
ossia se pur rimanendo complesso l'indice di rifrazione, si ha che la parte reale prevale nettamente sulla parte immaginaria, si ottiene che le superfici equifase e le superfici equiampiezza coincidono, ![]() e
e 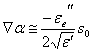 , sostituendo tali espressioni nell'equazione del trasporto si trova
, sostituendo tali espressioni nell'equazione del trasporto si trova 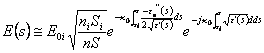 e quindi si ha anche un esponenziale reale che attenua il campo al crescere di s . In particolare viene definita l'attenuazione specifica del mezzo all'ascissa s
e quindi si ha anche un esponenziale reale che attenua il campo al crescere di s . In particolare viene definita l'attenuazione specifica del mezzo all'ascissa s ![]() e l'attenuazione
e l'attenuazione 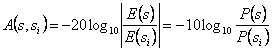 subita dal campo nel percorso tra si ed s .
subita dal campo nel percorso tra si ed s .
19) Onda non omogenea :
Si tratta di un´onda per la quale le superfici d´onda sono in ogni punto ortogonali alle superfici d´ampiezza.
