Onde piane

1) Caratteristiche delle onde in un mezzo uniforme :

Se il mezzo è uniforme si ha che l'indice di rifrazione non è funzione del punto e quindi  e pertanto le traiettorie sono rettilinee quindi le superfici d'onda possono essere piani, sfere, cilindri  ,  inoltre essendo   costante si ha che le equazioni delle onde sono a coefficienti costanti.

 

2) Caratteristiche delle onde piane in un mezzo uniforme :

Un'onda con superfici d'onda piane ha espressione  , sostituendola nell'equazione delle onde si ottiene 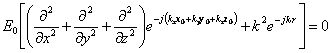 , derivandola e ricordando che l'esponenziale non si annulla mai, si ricava la condizione     ma       , si ha cioè l'uguaglianza     sulla quale si fanno le seguenti considerazioni :

a)       se e è reale allora deve essere   il che accade se il mezzo è non dissipativo (a=0) o se a ^ b

b)       se e è complessa allora deve essere .

Nella forma più generale comunque l'onda può essere scritta    dove   è il fattore di ampiezza  ed il vettore di attenuazione a individua i piani equiampiezza mentre  è il fattore di fase ed il vettore di fase b individua i piani equifase.

 

3) Caratteristica delle onde piane uniformi e non uniformi in un mezzo uniforme :

Un'onda piana uniforme è caratterizzata da piani equiampiezza coincidenti con i piani equifase, il che avviene se a=0 o     a // b , la velocità di fase nella direzione di r₀ è     da non confondere con la velocità di propagazione dell'onda che è la velocità di fase nella direzione di b₀ e che naturalmente è la minima in quanto rende massimo il denominatore. Il valore della velocità di fase dipende oltre che dalla direzione considerata rispetto a b₀ anche dalla uniformità o meno dell'onda, infatti per un'onda uniforme (a=0 oppure a//b) si ha   mentre per un'onda non uniforme (a¹0)  si ha     .

4) Relazioni tra campi e vettore di propagazione per un'onda piana :

Sostituendo le  espressioni dei campi relativi ad un´onda piana    e    nella  ed utilizzando la relazione vettoriale   con    ed  si  ottiene   . Un risultato analogo si ottiene dalla  semplificando e riordinandole si ottengono      e                 ossia dei prodotti vettoriali tra grandezze complesse che si semplificano soltanto nel caso dell'ondapiana uniforme (a=0 oppure a//b) si ottiene infatti 

                                e                            

5) Parametri secondari :

a)  k                         determina le caratteristiche di propagazione e di trasporto

b)  h                       determina il rapporto tra la ampiezza del campo elettrico e la ampiezza del campo magnetico

 

6) Considerazioni sulla costante di propagazione nel caso di mezzo percorso da correnti di conduzione ma privo di dissipazioni dielettriche o magnetiche :

La costante di propagazione ha componenti 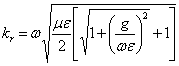  e 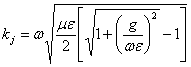   da cui si nota che se le correnti di spostamento prevalgono sulle correnti di conduzione ossia se si ha   allora il mezzo si comporta come un dielettrico altrimenti si comporta come un conduttore   , si osservi che in alta frequenza il mezzo tende a comportarsi come un dielettrico.

 

7) Considerazioni sulla costante di propagazione nel caso di mezzo percorso da correnti di conduzione ma privo di dissipazioni dielettriche o magnetiche :

Essendo |e''| << e'  nei casi reali, dalla   , si ottengono     e    in particolare si osserva che il mezzo può divenire dissipativo se w è molto alta anche se e'' è infinitesimo.

 

8) Impedenza intrinseca per un´onda piana uniforme :

L'espressione della impedenza intrinseca è   , considerando le sole dissipazioni dovute alla conducibilità (e'' = 0) si ottengono          e 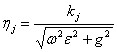          quindi se il mezzo si comporta da dielettrico (we>>g)  si ha   mentre se si comporta da conduttore (g>>we) si ha  e quindi tende a zero quando la conducibilità g tende ad infinito come avviene per un conduttore.

 

 

9) Parametri di Stokes :                      

                                                             

soltanto 3 dei parametri di Stokes sono indipendenti in quanto si ha    inoltre questi ultimi possono anche essere espressi in funzione dei parametri di polarizzazione :

                                 

 

10) Sfera di Poincare :

Ad ogni punto su tale sfera corrisponde una diversa polarizzazione e viceversa, in particolare si ha :

a)       ai punti sull´equatore (c=0) corrisponde una polarizzazione lineare, ad esempio al punto di intersezione tra la sfera e il semiasse positivo delle x corrisponde una polarizzazione lineare orizzontale (y=0) mentre al punto d´intersezione tra la sfera ed il semiasse negativo delle x corrisponde una polarizzazione lineare verticale (y=90°) .

b)       al polo Nord (c=45°) corrisponde una polarizzazione circolare sinistra mentre al polo Sud corrisponde una polarizzazione circolare destra.

c)       per i punti della emisfero Nord si ha una polarizzazione ellittica sinistra mentre per i punti della emisfero Sud si ha una polarizzazione ellittica destra.