Dispersione

1) Velocità di fase e di gruppo di un campo quasi monocromatico:

Considerando presente il solo termine dominante E₀(s) nello sviluppo di Luneburg-Kline e supponendo che sia reale, si ha che l'espressione del campo in funzione del tempo e di s è   la j è in questo caso ignota pertanto la si approssima al 1° ordine mediante Taylor   e sostituendo anche  si ha 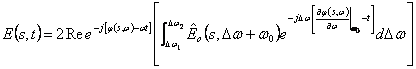  dove il 1° esponenziale è relativo ad una grandezza periodica con pulsazione w₀ che si propaga con velocità di fase  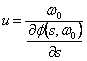mentre il 2° esponenziale modula nello spazio e nel tempo il 1° esponenziale, ed è detto inviluppo , ad esso corrisponde una velocità di gruppo  .

2) Condizione di uguaglianza tra velocità di fase e di gruppo :

Uguagliando velocità di fase e velocità di gruppo e portando i denominatori al numeratore del membro opposto, si ottiene   la quale è verificata se   , sostituendo in essa    e semplificando si ottiene    e quindi    la quale è verificata solo se l'indice di rifrazione non dipende da w.

 

3) Propagazione di un campo non monocromatico :

Si considera una portante a frequenza w₀ modulata in ampiezza da un impulso gaussiano avente durata iniziale  pertanto l'espressione del campo   , scrivendo il coseno in forma esponenziale si ricava la trasformata di Fourier nel punto iniziale 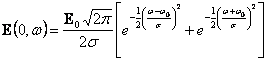  cpstituita da due bande gaussiane di ampiezza 4s centrate su -w₀  e su w₀ . Il valore della trasformata di Fourier nel punto s si ricava moltiplicando per   , antitrasformandola si ottiene   essa contiene la funzione eiconale la quale è incognita , tuttavia per il 1° integrale può essere sostituita con uno sviluppo in serie arrestato al 2° ordine   ottenendo   nel quale effettuando la sostituzione   e successivamente    e     si ottiene, sempre per il 1° integrale .  Analogamente si procede per il 2° integrale dove stavolta per coerenza con le posizioni precedenti per la funzione eiconale si ha lo sviluppo   dove il meno presente sulla derivata prima determina la definizione di grandezze coniugate rispetto alle precedenti e quindi si ottiene, per il 2° integrale, . Sostituendo i due risultati trovati ed ricordando che   si ha  .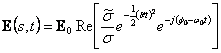

 

4) Fattore di ampiezza :

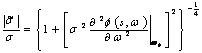
quindi con la aumentare della distanza percorsa diminuisce la ampiezza del campo.

 

5) Fattore di trasporto :

ad esso è legata la forma della impulso che è ancora gaussiano ma cambia la sua ampiezza che è maggiore dopo la propagazione. È chiamato fattore di trasporto in quanto in esso sono presenti sia il tempo che lo spazio e quindi si può ricavare la velocità della impulso gaussiano che si trova esser pari alla velocità di gruppo.

 

6) Durata della impulso :

  quindi con la aumentare della distanza percorsa aumenta la durata della impulso.

 

7) Differenza tra un mezzo dissipativo ed un mezzo dispersivo :

Si ha che il mezzo dissipativo trasforma energia elettromagnetica in calore per effetto Joule mentre un mezzo dispersivo non trasforma energia elettromagnetica in un´altra forma d´energia ma semplicemente la ridistribuisce nello spazio, pertanto se inviamo un impulso in un mezzo dispersivo esso si allarga e diminuisce la ampiezza del campo.